一种非全对称低耦合度三平移一转动并联机构的设计及其运动学

沈惠平 许 可 杨廷力 邵国为

常州大学现代机构学研究中心，常州,213016

0 引言

KRUT等提出了一类可实现3T1R的四自由度I4L[1]、I4R[2]、Par4[3]、Heli4[4]并联机器人，其中，I4机械手在两相邻支链末端安装子平台，两子平台通过齿轮齿条传动，将两子平台间的相对移动转化为末端执行器绕z轴的转动，但这种结构使动平台整体尺寸增大；赵铁石等[5]提出了一种4-URU型3T1R并联机器人构型；杨廷力等[6]基于单开链理论提出了一类3T1R并联构型；黄田等[7]发明了3种Cross-IV的3T1R型四自由度高速并联机械手；刘辛军等[8]研制出具有一个动平台的X4型并联机器人样机；FANG等[9]基于螺旋理论，提出了具有相同支链的4-DOF和5-DOF的并联机构；ANCUTA等[10]提出了一种实现Schönflies运动的λ-四滑块四自由度并联机构，并给出了该机构的位置正反解、机构奇异位形和工作空间分析；RICHARD等[11]对一种部分解耦的3T1R并联操作手样机进行了运动学分析。

上述3T1R机构具有如下特点：①4条支链结构完全相同，多为约束支链，制造、装配较复杂；②4条支链对静平台的几何中心(或2条以上中心线)完全对称布置(简称全对称)；③耦合度κ较大，为κ=2[12]，机构位置正解、动力学求解较为复杂。

为此，本文首先提出一种含不同支链结构(2条约束支链、2条无约束支链)的3T1R并联机构，且仅对静平台的对角线对称布置(简称非全对称)，耦合度较高(κ=2)。为此，采用拓扑结构降耦方法来使机构的耦合度降至为1，但保持其基本功能——方位特征(position and orientation characteristics, POC)及自由度(degree of freedom, DOF)不变；然后，给出了该降耦机构位置正解求解的一维搜索法及其数值解；最后，分析了该降耦机构的工作空间、转动能力及奇异性条件。

1 基于POC方程的并联机构拓扑设计理论[13]

机构末端运动输出的POC方程为

(1)

(2)

式中，MJi为第i个运动副的方位特征集；Mbi为第i条支链末端的POC集；MPa为机构动平台的POC集。

并联机构的自由度公式为

(3)

(4)

由基于有序单开链(single-open-chain，SOC)的机构组成原理知，任一机构可分解为一系列约束度为正、零、负的三种有序单开链，单开链可视为断开了某个构件的回路，因此，第j个SOC的约束度定义为

(5)

式中，mj为第j个SOC的运动副数；fi为第i个运动副的自由度(不含局部自由度)；Ij为第j个SOC的驱动副数。

进一步，一组有序的υ个SOC可组成一个独立回路数为υ的基本运动链(basic kinematics chain，BKC)，对一个BKC而言，须有

因此，其耦合度为

(6)

2 3T1R机构设计及其拓扑特性分析

2.1 3T1R机构的设计及特点

由式(1)所示的串联机构的POC方程的“并运算”规则易知，图1a所示的含4个球副S的平行四边形复杂支链未端产生的POC集为三平移两转动(3T2R)，两转动(2R)的轴线分别为R21、R22的轴线；由式(2)所示的并联机构的POC方程的“交运算”规则知，当2条这样的3T2R复杂支链在静平台0上的转动副轴线不平行(R21、 R11不平行)时，即可消除其一个转动而保持绕动平台1法线(R22或R12)的转动，从而获得3T1R输出；进一步，因该机构的自由度为4，为使每条支链仅具有1个驱动副，其他的2条支链可由S-P-S、S-S-R等无约束支链来实现，因此，本文提出的非全对称3T1R机构如图1b所示[14-15]。

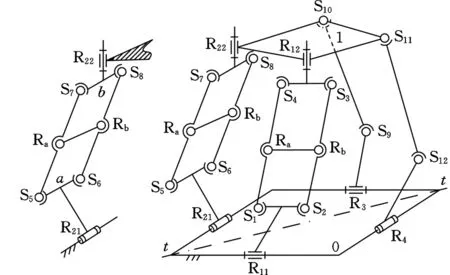
(a)产生3T2R的复杂支链(b)3T1R机构图1 3T1R并联机构设计Fig.1 The design of a novel 3T1R parallel mechanism

这样，该机构的静平台0与动平台1之间仅用2条相同的含4个球副的平行四边形复杂支链及2条S-S-R型无约束支链连接；静平台0上的R21与R11垂直布置，R3与R4可任意布置。从整体上看，该机构仅相对于静平台的对角线直线t-t对称，与具有4条含4S的平行四边形复杂支链的H4、IR4、Par4、X4等完全对称机构相比，对称性已有降低，介于完全对称与完全不对称之间，称为非全对称，但结构简单，制造成本降低，装配容易。

2.2 3T1R机构的拓扑特性分析

2.2.1确定并联机构动平台的POC集

4条支链的拓扑结构分别为bi：{Ri1(-:(4S))⊥Ri2}(i=1,2)；b3：{R3-S9-S10}；b4：{R4-S12-S11}。

选定动平台1上的基点O′。确定支路末端构件的POC集。因平行四边形(4S)的运动输出等价于2T1R，所示由式(1)得

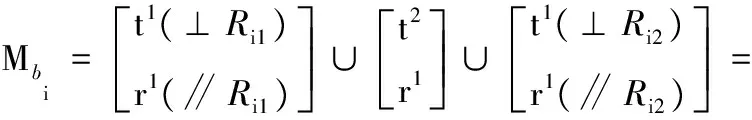
由式(2)得动平台POC集：

因此，动平台1可实现三平移一转动输出。

2.2.2确定并联机构自由度

此机构可分解为3个独立回路：

SOC1{-R11(-(4S))⊥R12∥R22(-(4S))⊥R21}

SOC2{-R3-S9-S10-}

SOC3{-R4-S12-S11-}

(1)确定第一个回路的独立位移方程数ξL1。由式(3)、式(4)得

(2)确定第二个回路的独立位移方程数ξL2。由式(3)、式(4)得

(3)确定第三个回路的独立位移方程数ξL3。由式(3)得

(4)确定并联机构自由度。由式(4)得

因此，当选取静平台0上的4个转动副R11、R21、R3、R4为主动副时，动平台1可实现三平移一转动输出。

2.2.3确定并联机构耦合度κ

确定SOC1、 SOC2、 SOC3的约束度。因2.2.2节已求得各回路的独立位移方程数，即ξLj=6(i=1，2，3)，因此，由式(5)得它们的约束度：

由式(6)得

可见，该机构仅包含一个BKC，但耦合度仍较高(κ=2)，因此，机构位置正解还较复杂[16]。为此，可通过机构拓扑结构降耦方法，将其耦合度降低为1，使其位置正解易用一维搜索法求出，而保持机构的运动输出类型和自由度不变，即方位特征仍为三平移一转动。

3 3T1R并联机构的结构降耦设计

3.1 降耦机构的设计及POC集分析

现根据并联机构的结构降耦原理和方法[17]，将动平台1上两条复杂支链末端R12副与R22副轴线重合，从而构成一条混合支链；两条无约束S-S-R支链上的布置不变，这样，可使机构耦合度从2降至为1，但其方位特征和自由度不变,简称为降耦机构[18]。降耦后的机构仍仅关于静平台对角线t-t对称，也为非全对称，如图2所示。此时，该机构的三条支链为

b1：{-R11(-(4S))-R12⊥((4S))R21-R22}

b2：{-S10-S9-R3-}

b3：{-R4-S12-S11-}

图2 低耦合度的3T1R降耦机构(κ=1)Fig.2 3T1R coupling-reducing PM(κ=1)

选定动平台1上的基点O′，如图2所示，确定支路末端构件的POC集。由式(1)，得

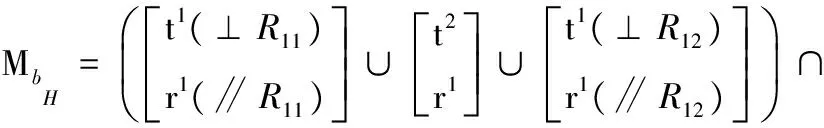
确定动平台POC集。由式(2)，得

因此，动平台1仍可实现三平移、一转动输出。

3.2 降耦机构的自由度分析

降耦机构的三个独立回路为

SOC1{-R11(-(4S))-R12⊥(4S)⊥R21-}

SOC2{-R22-S10-S9-R3-}

SOC3{-R4-S12-S11-}

(1)确定第一回路的独立位移方程数ξL1。由式(3)、式(4)得

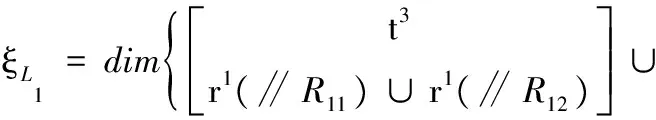
(2)确定第二回路的独立位移方程数ξL2。第二回路由SOC1、SOC2组成，也可看作由混合支链b1和无约束支链b2构成，由式(3)、式(4)得

(3)确定第三独立回路的独立位移方程数ξL3。由式(3)、式(4)得

(4)确定并联机构自由度。由式(4)得

因此，当选取静平台0上的4个转动副R11、R21、R3、R4为主动副时，动平台1仍可实现三平移一转动输出。

3.3 降耦机构的耦合度κ计算

同样，由式(5)，分别得确定SOC1、SOC2、SOC3的约束度：

由式(6)得

可见降耦机构也仅包含一个BKC，但其耦合度已降低为1。因此，用基于序单开链的一维搜索法较易求得其位置正解。

4 降耦机构的位置分析

4.1 序单开链法的位置正解求解原理

由式(5)、式(6)可知，单开链的约束度Δj为正值、零、负值三种形式，其物理意义是：

4.2 机构坐标系的建立与参数标注

如图3所示，该机构静平台0为正方形，边长为2l1；动平台1为等边三角形，边长为l2。与静平台0相连接的4个转动副R11、R21、R3、R4分布在各边的中点。

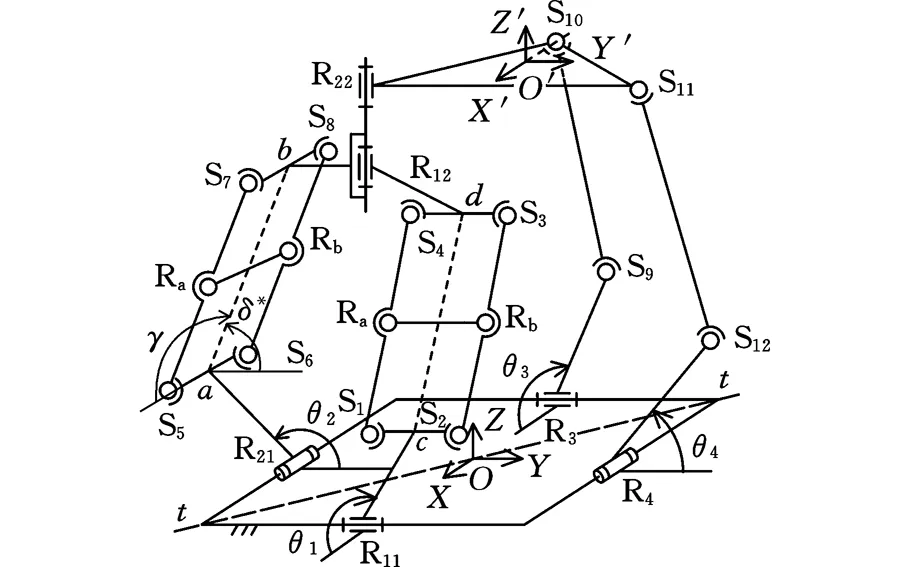
图3 降耦机构的结构参数及其标注Fig.3 Structure parameters of coupling-reducing PM

不失一般性，在静平台0上建立坐标系OXYZ，O为静平台的重心，X轴垂直于R11的轴线，Y轴平行于R11的轴线，Z轴由右手笛卡儿坐标系法则确定；在动平台1上建立坐标系O′X′Y′Z′，O′为动平台1的重心，X′轴垂直于R22S11，Y′轴与R22S11平行，Z′轴由右手笛卡儿坐标系法则确定。设R11c、R3S9和X轴正向的夹角分别为θ1、θ3；R21a、R4S12与Y轴正向的夹角分别为θ2、θ4；又设平行四边形S5S6S7S8平面与Y轴正方向的夹角为虚拟角δ*，ab与X轴正方向的夹角为γ。

为理解方便，将图3所示机构展开，得到其平面展开俯视图(图4)。其中，dR12和S3S4的夹角、和S8S7的夹角均为固定角β。设混合支链的各杆长分别为：R11c=R21a=l3，ab=cd=l4，R12b=R12d=l5，R22R12=l6；两条无约束支链的杆长分别为R3S9=R4S12=l7，S9S10=S11S12=l8；设动平台O′的坐标为(x，y，z)，R22S11与Y轴正向的夹角为动平台姿态角α。

图4 机构构型的俯视展开表达Fig.4 Expression of top view for decoupling mechanism

4.3 位置正解求解

已知输入角θ1、θ2、θ3、θ4，求动平台1上O′的坐标(x，y，z)和转角α。

易知，在静坐标系OXYZ下，静平台1上的4个转动副R11、R21、R3、R4的坐标分别为(l1,0,0)、(0,-l1,0)、(-l1,0,0)、(0,l1,0)；点c、a及球副S9、S12的坐标分别为(l1+l3cosθ1，0，l3sinθ1)、(0，l3cosθ2-l1，l3sinθ2)、(l7cosθ3-l1，0，l7sinθ3)、(0，l1+l7cosθ4，l7sinθ4)。

(1)在Δ1>0的SOC1上，设定虚拟变量δ*，并求解中间变量γ。对于SOC1{-R11(-(4S))-R12⊥((4S))R21-}，点b、d及转动副R12的坐标由几何法求得

(7)

(8)

(9)

注：*表示与虚拟角δ*有关，下同。

由cd=l4，建立约束方程：

整理并化简得

Asinγ+Bcosγ+C=0

(10)

令tanγ/2=u，则有

(11)

(12)

(13)

则动平台上R22的坐标为

(14)

由式(8)、式(14)，可得

(15)

同理，可得动平台1上S10、S11的坐标：

(16)

(17)

由S10S9=l8，建立约束方程：

整理并化简得

Esinα+Fcosα+G=0

(18)

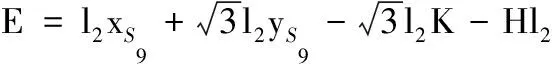
令tanα/2=tα，解得

(19)

(3)在Δ3<0的SOC3上，建立约束方程。对于SOC3{-R4-S12-S11-}，根据式(15)、式(17)，由S11S12=l8，建立位置约束方程：

(20)

通过一维搜索，改变虚拟角δ*的赋值，直至满足式(20)，获得真实的δ；将其代回位置正解求解式(6)～式(18)，即可求出各个运动副位置的真实值，从而得到该机构的位置正解。

4.4 位置逆解求解

已知动平台1上O′的坐标(x，y，z)和转角α，求输入角θ1、θ2、θ3、θ4。

4.4.1求机构各点坐标

根据式(12)、式(13)，可得点b、d的绝对坐标：

(21)

(22)

球副S10、S11的绝对位置坐标，见式(16)、式(17)。

4.4.2建立位置相容方程

由杆长条件，建立以下位置约束方程：

(23)

(24)

(25)

(26)

4.4.3求输入角θ1、θ2、θ3、θ4

由式(23)～(26)，可得

(27)

i=1,2,3,4

t1=l3zdt2=l3zbt3=l7zS10t4=l7zS11

综上可知，当动平台O′的坐标(x，y，z)和转角α已知时，输入角θ1、θ2、θ3、θ4各有两组解。故逆解数为16，因此，机构有16种构型。

4.5 正逆解验证

参考ABB机器人I4R的结构参数，本机构的2个平行四边形的尺寸参数取与之相同[19]，即l1=l2=400 mm，l3=l5=l7=375 mm，l4=l8=800 mm，l6=100 mm，β=90°。

输入角(θ1，θ2，θ3，θ4)分别取两组数据：数据Ⅰ(43.211 5°，141.543 3°，111.793 3°，66.921 9°)；数据Ⅱ(50°，120°，120°，60°)。

由MATLAB计算得机构位置正解，见表1。

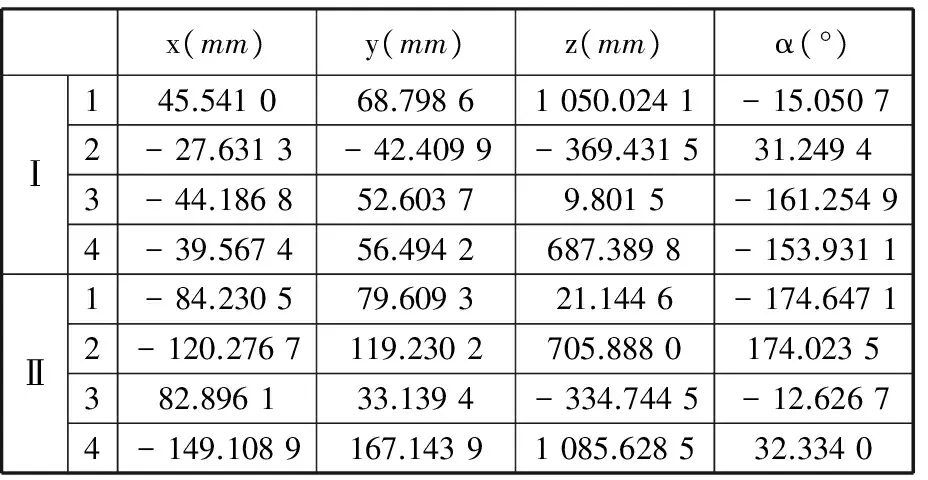
表1 机构的位置正解

取Ⅰ中第1组的正解数值，代入到逆解求解公式(式(27))中，得到θ1、θ2、θ3、θ4的16组逆解，如表2所示。

表2机构的位置逆解

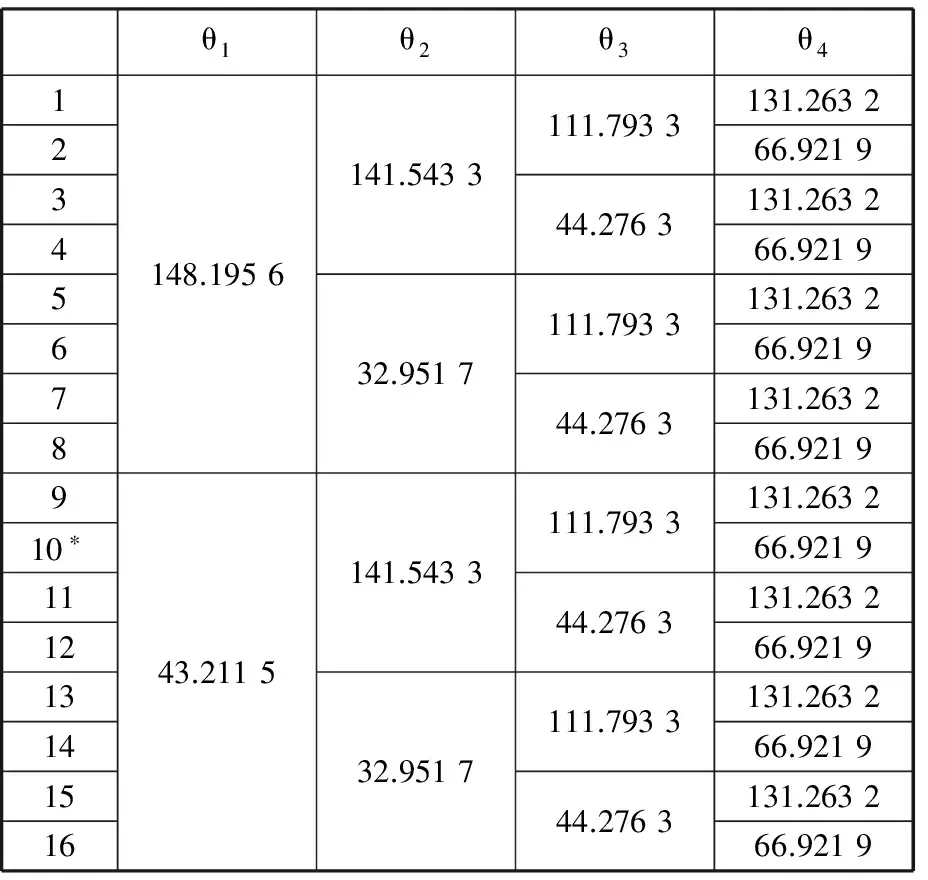
Tab.2 Numerical solutions of the inverse kinematics (°)

表2中，第10组数据θ1=43.211 5°，θ2=141.543 3°，θ3=111.793 3°，θ4=66.921 9°，和正解求解时第Ⅰ组的4个输入角一致；同样，用第Ⅱ组中的正解数据，也验证了4个输入角的一致性，因此，正逆解公式导出正确。

5 降耦机构的工作空间和转角能力分析

5.1 工作空间分析

降耦机构动的工作空间分析，采用极坐标三维搜索法[20]。先将搜索范围限制在：300 mm≤z≤1 200 mm，-π≤θ≤π，0≤ρ≤1 000 mm；运用MATLAB软件编程，得到降耦机构工作空间的三维立体图(图5)，图6为Z向不同高度的X-Y截面图。

(a)z=300 mm(b)z=460 mm

(c)z=700 mm(d)z=900 mm图6 降耦机构工作空间的Z截面图Fig.6 Cross-section of the workspace

图5、图6可以看出：

(1)该机构工作空间整体呈近似圆柱状，对称性较好，表面光滑。

(2)当300 mm≤z≤460 mm时，该机构的工作空间X-Y截面图不连续，存在空洞；当460 mm≤z≤1 175 mm时，截面连续，且形状比较规则，轮廓圆滑；从z=460 mm开始，随着高度的增加，截面面积逐渐减小。

(3)与同类3T1R机构工作空间体积的比较，由文献[19]，不考虑转动副的转角约束，当高度500 mm≤z≤1 200 mm时，本文计算出I4R机构与降耦机构的工作空间体积分别为6.168 8×108mm3、7.556 3×108mm3；由文献[21]，当高度766 mm≤z≤1 016 mm时，Cross IV-3机器人与降耦机构工作空间体积分别为4.427 4×108mm3、5.152 9×108mm3。

因此，降耦机构比I4R、CrossIV-3工作空间分别增加了22.53%、16.39%。

5.2 转动能力分析

转动能力分析就是评估并联机构动平台的转动角度范围，当并联机构动平台基点处于工作空间内某一位置时，其姿态角存在一定范围。根据逆解公式，采用极限边界搜索法，可求出基点处于工作空间内任一点时的转角范围。

现取z=1 000 mm，分别计算降耦机构和H4机构[22](动平台未加齿轮传动)在工作空间内X-Y平面上各点转角最大值αmax与最小值αmin(单位为(°))的分布，如图7所示。

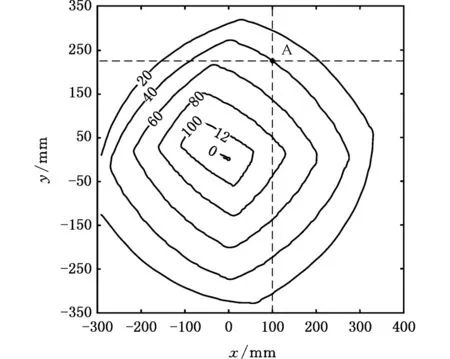
(a)H4机构的αmax分布

(b)H4机构的αmin分布

(c)降耦机构的αmax分布

(d)降耦机构的αmin分布

分别取两机构工作空间内的相同位置，例：A(100,225,1 000)，得H4机构、降耦机构在该点位置的转角范围分别为[-40°,40°](图7a、图7b)、[-40°,102°](图7c、图7d)，因此，降耦机构转角范围增加了77.5%。

同样，用该方法可求得这两机构在工作空间内其他位置的转角范围，对比得：降耦机构的转角范围大，因此，降耦机构动平台无需特殊转动放大装置，便可获得较大的转角范围。

6 降耦机构的奇异性分析

6.1 机构奇异性分析方法

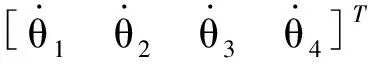
JpV=Jqω

(28)

Jq=diag(u11，u22，u33，u44)

f11=xd-xc

f12=yd-yc

f13=zd-zc

f21=xb-xa

f22=yb-ya

f23=zb-za

f31=xS10-xS9

f32=yS10-yS9

f33=zS10-zS9

f41=xS11-xS12

f42=yS11-yS12

f43=zS11-zS12

u11=(zd-zc)l3cosθ1-(xd-xc)l3sinθ1

u22=(zb-za)l3cosθ2-(yb-ya)l3sinθ2

u33=(zS10-zS9)l7cosθ3-(xS10-xS9)l7sinθ3

u44=(zS11-zS12)l7cosθ4-(yS11-yS12)l7sinθ4

依据Jp、Jq矩阵是否奇异，将机构的奇异位形分为如下三类：①det(Jq)=0时，机构发生输入奇异；②det(Jp)=0时，机构发生输出奇异；③det(Jq)=det(Jp)=0时，机构发生综合奇异。

6.2 奇异性分析

6.2.1输入奇异

当机构发生输入奇异时，机构的动平台将失去某个方向的运动能力，此时，至少有一个运动链到达了工作空间的边界。此时det(Jq)=0，方程解的集合为

U={U1∪U2∪U3∪U4}

(29)

U1={(zd-zc)cosθ1-(xd-xc)sinθ1=0}，即R11、c、d三点共线；

U2={(zb-za)cosθ2-(yb-ya)sinθ2=0}，即R21、a、b三点共线；

U3={(zS10-zS9)cosθ3-(xS10-xS9)sinθ3=0}，即R3、S9、S10三点共线；

U4={(zS11-zS12)cosθ4-(yS11-yS12)sinθ4=0}，即R4、S12、S11三点共线；

例1 满足子集U4的三维构型如图8所示。

图8 输入奇异位形Fig.8 The input singularityof coulping-reducing PM

此时，支链R4-S12-S11已经到达该支链的运动极限位置，即动平台已经到达机构工作的空间边界。

6.2.2输出奇异

当所有的主动件锁住时，动平台依旧可以产生局部运动，称为机构发生输出奇异。此时，若机构动平台上作用有限的力，则主动件上将需无穷大的驱动力才能达到力平衡。矩阵Jp的每一行的前三个元素即对应一个向量，取

(f11,f12,f13)=cd

(30)

(f21,f22,f23)=ab

(31)

(f31,f32,f33)=S9S10

(32)

(f41,f42,f43)=S12S11

(33)

若det(Jp)=0，则向量cd、ab、S9S10、S12S11有如下两种情况：①至少有两个向量相互平行；②至少有三个向量线性相关。其中，两个向量平行的几何意义是：当ab∥S9S10时，有

式中，η为常系数。

整理得

(34)

对应的三维构型如图9所示。

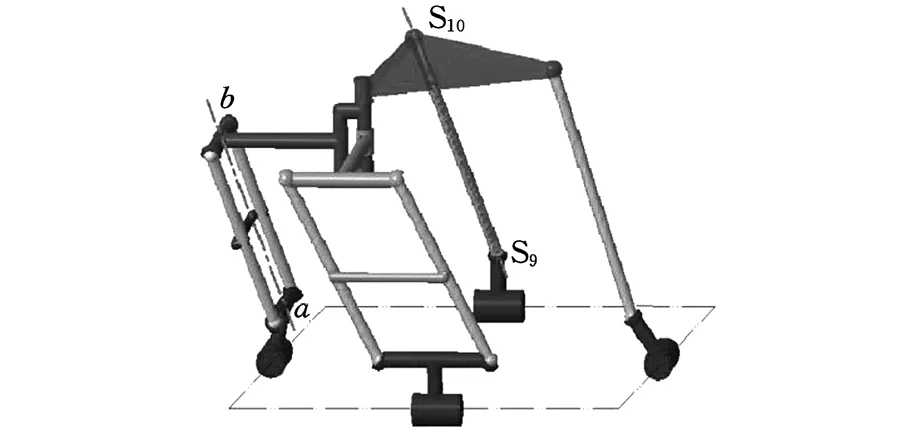
图9 输出奇异位形举例(ab∥S9S10)Fig.9 Output singularity of coupling-reducing PM (ab∥S9S10)

即det(Jp)=0，对应的三维构型如图10所示。

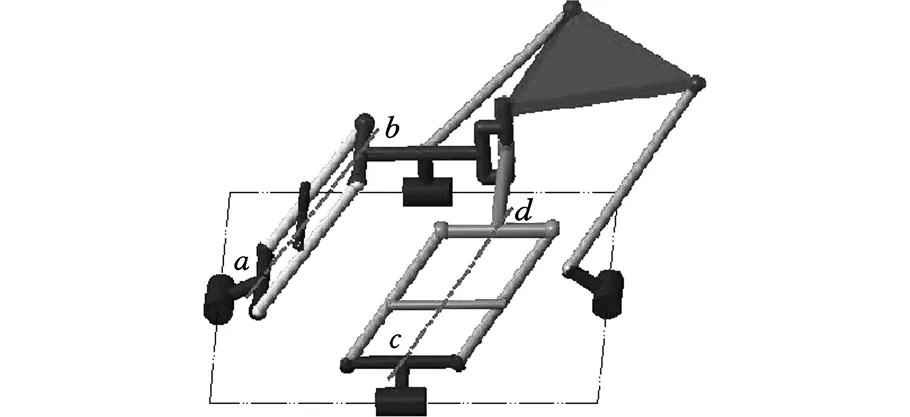
图10 输出奇异位形举例(ab∥cd)Fig.10 Output singularity of coupling-reducing PM(ab∥cd)

6.2.3综合奇异

综合奇异时，det(Jq)=det(Jp)=0，即输入奇异和输出奇异同时发生。机构满足U4且ab∥S9S10，则机构满足R4、S12、S11三点共线且满足式(33)，其三维构型，如图11所示。

图11 机构的综合奇异位形举例Fig.11 Synthetic singularity of coupling-reducing PM

7 结论

(1)设计出一种非全对称、低耦合度(κ=1)的3T1R并联操作手，并求解了其位置正逆解。

(2)工作空间分析表明：当460 mm≤z≤1175 mm时，该机构工作空间较规则，呈近似圆柱状且连续；进一步，工作空间体积比相同参数的I4R机构大22.53%，比Cross IV-3大16.39%；同时，其转角范围大于同类3T1R的H4机构等。

(3)通过奇异位形分析，得到了降耦机构发生输入奇异、输出奇异和综合奇异的条件。

(4)降耦机构含2条无约束支链，结构简单、制造装配方便，具有一定的研发价值。

[1] KRUT S，BENOIT M，OTA H，et al.I4：a New Parallel Mechanism for Scara Motions[C]//2003 IEEE International Conference on Robotics and Automation.Taipei，2003：1875-1880.

[2] KRUT S，NABAT V，PIERROT F.A High-speed Parallel Robot for Scara Motions [C]//2004 IEEE International Conference on Robotics and Automation.New Orleans，2004：4109-4115.

[3] NABAT V，RODRIGUEZ M，KRUT S，et al.Par4：Very High Speed Parallel Robot for Pick-and-place[C]// IEEE/RSJ International Conference on Intelligent Robots and Systems.Edmonton，Canada，2005：553-558.

[4] KRUT S，NABAT V，PIERROT F.Heli4：a Parallel Robot for Scara Motions with a Very Compact Traveling Plate and a Symmetrical Design[C]//2006 IEEE/RSJ International Conference on Intelligent Robots and Systems. Beijing，2006：1656-1661.

[5] 赵铁石，黄真.欠秩空间并联机器人输入选取的理论和应用[J].机械工程学报，2000，36(10)：81-85.

ZHAO Tieshi，HUANG Zhen.Theory and Application of Selecting Actuating Components of Spatial Parallel Mechanisms[J]. Chinese Journal of Mechanical Engineering，2000，36(10)：81-85.

[6] 杨廷力，金琼，刘安心.基于单开链单元的三移动一转动并联机器人机构型综合及机构分类[J].机械工程学报，2002，38(8)：1038-1043.

YANG Tingli，JIN Qiong，LIU Anxin.Structural Synthesis and Classification of the 3dof Translational Parallel Robot Mechanisms Based on the Units of Single-opened-chain[J]. Chinese Journal of Mechanical Engineering，2002，38(8)：1038-1043.

[7] 黄田，赵学满，梅江平，等.一种具有三维平动一维转动的并联机构: 中国，ZL201220007884.X[P]. 2012-11-14.

HUANG Tian，ZHAO Xueman，MEI Jiangping，et al.A Parallel Mechanism with Three Translations and One Rotation: China，ZL201220007884.X[P].2012-11-14.

[8] 刘辛军，谢富贵，王立平,等.一种可实现SCARA运动的四自由度单动平台并联机构: 中国，201210435375.1[P].2012-11-02.

LIU Xinjun， XIE Fugui， WANG Liping, et al.A Kind of Four Degrees of Freedom of Moving Platform Parallel Mechanism with SCARA Exercise: China，201210435375.1[P].2012-11-02.

[9] FANG Y F，TSAI L W.Structural Synthesis of 4-DOF and 5-DOF Parallel Manipulators with Identical Limbs[J].The International Journal of Robotics Research，2002，21(9)：799-810.

[10] ANCUTA A，COMPANY O，PIERROT F.Design of Lambda-Quadriglide：a New 4-DOF Parallel Kinematics Mechanisms for Schönflies Motion[C]//Proceedings of the ASME 2010 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference. Montreal，2010：1131-1140.

[11] RICHARD P L，GOSSELIN C，KONG X.Kinematic Analysis and Prototyping of a Partially Decoupled 4-DOF 3T1R Parallel Manipulator[C]//ASME International Design Engineering Technical Conferences & Computers & Information in Engineering Conference. Philadelphia，2006：1029-1036.

[12] 沈惠平，曾氢菲，李菊，等.典型并联机构拓扑结构特征分析[J].农业机械学报，2016，47(8)：388-398.

SHEN Huiping，ZENG Qingfei，LI Ju，et al.Topological Characteristic Analysis for Practical Parallel Mechanisms [J].T. Chin. Soc. Agric. Mach.，2016，47(8)：388-398.

[13] 杨廷力，刘安心，罗玉峰，等.机器人机构拓扑结构设计[M].北京：科学出版社，2012.

YANG Tingli，LIU Anxin，LUO Yufeng，et al.Theory and Application of Robot Mechanism Topology [M]. Beijing：Science Press，2012.

[14] 沈惠平，杨廷力，朱小蓉，等.一种三平移一转动并联机器人:中国，201510564382.5[P].2015-09-08.

SHEN Huiping，YANG Tingli，ZHU Xiaorong，et al.A Parallel Mechanism with Three Translations and One Rotation: China，201510564382.5[P].2015-09-08.

[15] YANG Tingli，LIU Anxin，SHEN Huiping，et al. Topological Structure Synthesis of 3T1R Parallel Mechanism Based on POC Equations[C]//Proceedings of 9th International Conference on Intelligent Robotics and Applications. Tokyo，2016：147-161.

[16] 沈惠平，尹洪波，王振，等.基于拓扑结构分析的求解6-SPS并联机构位置正解的研究[J].机械工程学报，2013，49(11)：14-20.

SHEN Huiping，YIN Hongbo，Wang Zhen，et al. Research on Forward Position Solutions for 6-SPS Parallel Mechanisms Based on Topology Structure Analysis[J]. Journal of Mechanical Engineering，2013， 49(11)：14-20.

[17] 沈惠平，朱小蓉，尹洪波，等.并联机构的结构降耦原理及其设计方法[J].机械工程学报，2016，52(23)：102-113.

SHEN Huiping，ZHU Xiaorong，YIN Hongbo，et al. Study on the Principle and Design method for Structure Coupling-reducing of Parallel Mechanisms[J].Journal of Mechanical Engineering，2016，52(23)：102-113.

[18] 李菊，沈惠平，强恒存，等.一种低耦合度三运动副动平台的三平移一转动并联机器人平台:中国，201610141614.0[P].2016-03-15.

LI Ju，SHEN Huiping，QIANG Hengcun，et al. A Low Coupling DegreeParallel Robot Platform with Three Translations and One Rotation: China， 201610141614.0[P]. 2016-03-15.

[19] 刘平松.I4R型并联机器人全域性能及其优化研究[D]. 南京：南京理工大学，2013.

LIU Pingsong.Global Performance and Optimization of I4R Parallel Robot[D].Nanjing ：Nanjing University of Science and Technology，2013.

[20] 黄真，孔令富，方跃法.并联机器人机构学理论及控制[M].北京：机械工业出版社，1997.

HUANG Zhen，KONG Lingfu，FANG Yuefa.Parallel Robot Mechanism Theory & Control[M].Beijing：China Machine Press，1997.

[21] 李玉航，梅江平，刘松涛，等.一种新型4自由度高速并联机械手动力尺度综合[J].机械工程学报，2014，50(19)：32-40.

LING Yuhang，MEI Jiangping，LIU Songtao，et al. Dynamic Dimensional Synthesis of a 4-DOF High-speed Parallel Manipulator[J]. Journal of Mechanical Engineering，2014，(19)：32-40.

[22] XIE Fugui，LIU Xinjun.Design and Development of a High-Speed and High-Rotation Robot with Four Identical Arms and a Single Platform[J].Mechanisms and Robotics，2015，7 (4)： 041015.