手指康复外骨骼机器人的结构优化设计
王 杰 管声启 夏齐霄
1.西安工程大学机电工程学院,西安,7100482.北京联合大学机器人学院,北京,100020
0 引言
随着疾病灾难导致的肢体运动障碍患者越来越多,康复医学与机器人学结合的康复机器人技术正逐渐成为国内外研究的热点[1]。手指康复外骨骼机器人是外骨骼机器人在医疗领域中的一项应用,其主要任务是辅助中风患者活动锻炼手指或手外伤患者进行术后的康复训练[2-6]。文献[7]以一种欠驱动式手指康复训练装置为例,分析了其机械机构,对手指运动学模型空间状态进行了结构的优化。德国特里尔大学研制的食指康复机械手优化了驱动方式,实现了机构的轻量化[8]。北京航空航天大学设计的四自由度精巧外骨骼式手指运动功能康复机器人通过钢丝绳对手指的各个关节进行单独双向驱动,利用移动轴承座上附带的滑动槽来调节各模块间距,以使执行系统的某些长度可调节[9]。哈尔滨工业大学设计的由3个外骨骼关节(基于对称齿轮齿条平行滑动机构)串联而成的手指运动的矫形装置[10],不仅可以实现手指各关节的良好转动,而且可以通过调节个别机械构件的位置,使其与不同长度的手指相匹配。意大利热那亚大学研制的HEXOSYS手指康复外骨骼机器人不仅实现了食指和拇指独立的屈伸动作和之间的闭合运动,还可以通过独立的驱动器控制每个关节[11]。手指康复外骨骼机器人结构多样,但普遍存在结构笨重、控制系统结构复杂的问题,限制了手指康复机器人的应用范围[12]。
针对以上问题,通过了解人手结构特点,基于平面连杆机构,设计了一种可适用于不同手指长度的欠驱动式手指康复外骨骼机器人,并对该机器人进行运动学分析,得到了一定机械尺寸在对应手指长度下的所有空间状态,进而对关键机械结构进行了优化。
1 结构建模
1.1 手指运动特性分析
一般情况下,手部至多能完成的两种运动是弯曲拉伸和内收外展。手指关节的弯曲伸展运动与内收外展运动之间有着特定的约束关系,即弯曲伸展运动完成之后,通常不会再有内收外展运动[8]。
如图1所示,除大拇指外,其他4个手指的关节可分为掌指关节MP、近侧指间关节PIP、远侧指间关节DIP,每个手指的MP处含有2个自由度,PIP和DIP处各含有1个自由度,大拇指共含2个自由度,因此整个手指共18个自由度[13]。
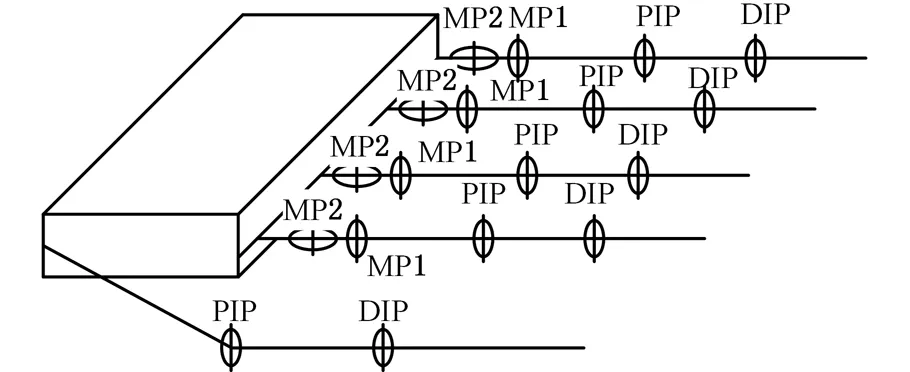
图1 手指自由度分析模型Fig.1 Analysis model of finger freedom
生物医学研究结果表明,手指运动的特点包括:①各段手指骨在同一平面内运动;②大拇指外伸的两段指骨在同一平面内运动;③MP处屈伸的轴线和内收外展的轴线几乎垂直;④PIP和DIP在运动时会相互影响;⑤各手指关节的弯曲范围和内收外展范围有限,例如掌指关节的弯曲角度一般都小于90°[11]。根据正常男女手指功能模型库,可得手指各个关节的运动角度,如表1所示。

表1 正常成人手指活动范围
1.2 机构组成与工作原理
该手指康复外骨骼机器人主要基于一种欠驱动连杆机构,其结构如图2所示,自由度为2。
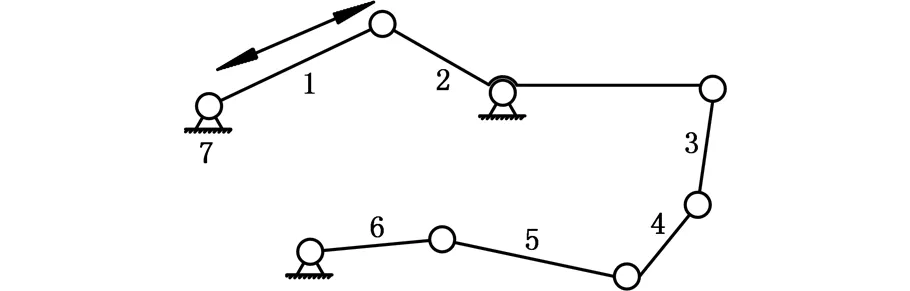
图2 机器人机构简图Fig.2 Schematic diagram of mechanism of robot
人的手指运动具有相同的特性,因此本文以食指为实验研究对象进行分析。如图3所示,手指的相关运动主要由掌骨、近指骨、中指骨、远指骨共同决定,并依次由掌指关节、近端指关节和远端指关节连接。根据前文提到的手指关节运动特点,基于平面连杆机构,设计了图3所示的一种由直线电机、弧形架、连杆及指套构成的终端牵拉式手指康复外骨骼机器人。康复训练中,该机器人通过和患者手指末端固连,从而带动手指其他关节实现目标屈伸运动,其中,A、I、B、G、F连接点均由铰链连接。
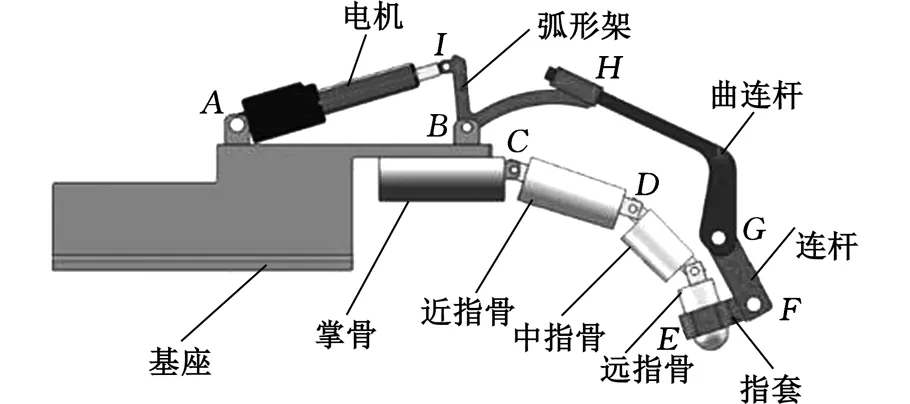
图3 机器人的设计模型Fig.3 Design model of robot
由机器人结构和手指组成系统的原动件数目小于自由度数目,因此决定了该手指康复外骨骼机器人含有不确定的终端运动,从而可以减小在康复过程中突发痉挛时机械结构带给患者的二次创伤。
2 优化设计
2.1 机械系统前端尺寸设计与优化
2.1.1模型简化
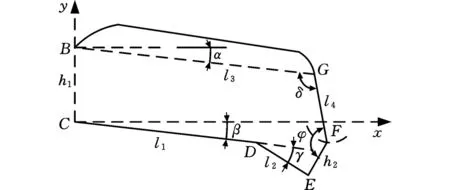
图4 前端机械结构及手指的简化运动模型Fig.4 Front end of the mechanical structure and simplified motion model of the finger
将图3所示的手指康复外骨骼机器人中的前端机械构件(弧形架、曲连杆、连杆及指套)和手指各个关节简化为图4所示的运动学模型。其中,近端指关节和掌指关节的转轴中心分别用C、D两点表示,E点是手指末端与手指套的垂足。由实际情况知,人手指的远指骨较短,因此,为了计算方便,可以忽略远指骨长度。掌指关节和近端指关节的弯曲角度分别用β、γ表示,α表示弧形架的转动角度,δ表示弧形架与连杆之间的夹角。向量(βi,γi,αi,δi)(i表示不同的状态,i=1,2,…,n)表示手指康复外骨骼机器人的前端机械构件和手指在空间的任一瞬时状态,把所有存在的空间瞬时状态称为空间瞬时状态集R。
因此,对手指康复外骨骼机器人的机械构件尺寸进行优化设计就可以转化为:使任一空间瞬时状态组成的空间状态集R包含手指在拉伸和弯曲过程中所有可能存在的空间状态。
2.1.2运动学分析
直线电机正常工作时,只要在合理范围内改变α,就可以根据图4中的几何关系并结合下式
(1)
由α唯一确定G点的坐标。由下式可知,
(2)
F点的位置可由δ确定。由于中指骨长度l2和指套高度h2为定值,且两者互相垂直,所以D、F两点的距离为
(3)
又C、D两点间的距离为l1,从而有
(4)
由D、E、F三点间的距离关系可得
(5)
在△BCD和△CDE中,由余弦定理可得
(6)
手指关节及前端机械结构的空间状态集R的求解过程为:①预设一α值,得G点坐标;②预设一δ值,并结合G点坐标,求得F点坐标;③根据F点坐标可以确定D、E点的坐标;④根据各点的位置关系可得β、γ;⑤令δ←δ+Δδ,重复过程②~④;⑥令α←α+Δα,重复过程①~⑤。经过上述过程,就可以得到手指及前端机械结构运动简化模型中的所有可能的向量(β,γ,α,δ),从而得到了空间瞬时状态集R。
手指及前端机械结构的各空间状态即空间瞬时状态集R由式(1)~式(6)确定。其中,α由直线电机直接控制,弧形架转动的范围越大,手指及前端机械结构的各空间状态就越多,越接近手指康复外骨骼机器人的理想状态,能适用于手指所有空间状态的可能性就越大。
2.1.3数值计算
给定手指长度,利用MATLAB对运动学模型的数值进行计算,求解出不同尺寸参数对应机械结构的运动学模型下的所有空间状态,并且从中找到某一组合理的尺寸,使得空间状态集R尽可能多地包含手指在屈伸过程中所有可能的空间状态。
对于事先给定的手指长度l1、l2和连杆长度l4,在确定手指康复外骨骼机器人的机械构件尺寸l3、h1和h2时,由于式(1)~式(6)中的变量较多,因此需要根据各个机械构件的实际情况对其尺寸进行预先的设定。由于要充分考虑手指康复外骨骼机器人的美观性和可穿戴性,所以应尽量减小h1和h2,为避免机械冲突和干涉,设定h1=25 mm,h2=20 mm,l4=40 mm。以l1=45 mm,l2=30 mm,60°≤δ≤120°为例,求得在式(1)~式(6)的限定条件下,不同l3对应手指的所有可能存在的空间瞬时状态,只取(β,γ,α,δ)中的β、γ绘制不同l3对应的手指空间状态,如图5所示。
假定手指在自然状态下屈伸时,β=-20°,γ=0°,即图5中的点(-20°,0°)。手指在目标屈伸状态时,β=60°,γ=80°,即图5中的点(60°,80°)。由计算结果可以看出:l3≤60 mm或l3≥80 mm时,对于当前给定手指长度,手指无法达到理想目标屈伸状态和自然状态下屈伸状态;65 mm≤l3≤75 mm时,手指可在自然状态下屈伸及目标屈伸状态之间活动。因此,在自然状态下,当给定一康复目标状态时,l3的长度必须有一定的范围,以保证不同手指长度的患者使用。
2.2 机械系统后端尺寸设计与优化
2.2.1模型简化与运动学分析
在实际工作情况中,直线电机只可在一定范围内推动弧形架转动有限的角度,因此很有必要对该手指康复外骨骼机器人的终端机械构件(直线电机、弧形架IB段及基座)进行结构优化,以便得到直线电机可推动弧形架转动足够大的角度,进而能满足达到前端机械结构所需。如图6所示,K1、K2分别为直线电机在该系统中工作时的两极限位置,θ、η分别为直线电机工作到两极限位置时与X轴的夹角,直线电机推动弧形架的实际转动角度为η-θ。 由图6可知,手指及终端机械结构应满足以下关系:
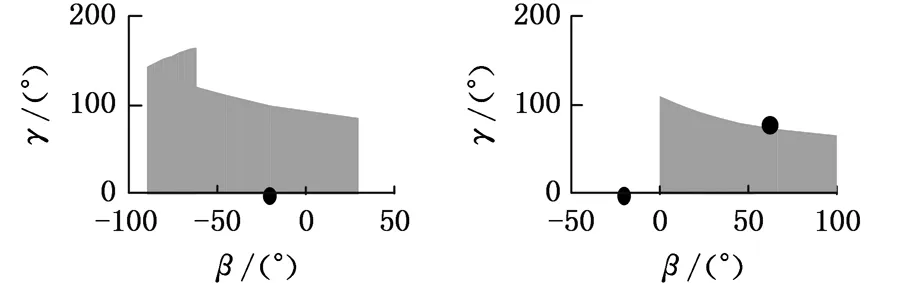
(a) l3=50 mm (b) l3=55 mm
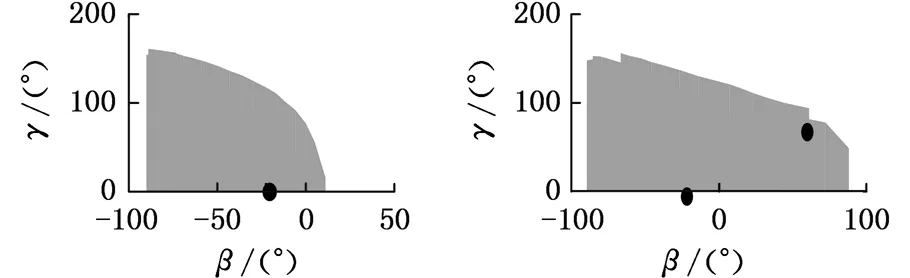
(c) l3=60 mm (d) l3=65 mm
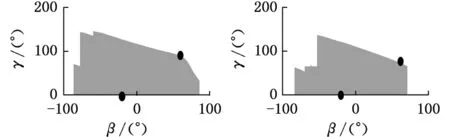
(e) l3=70 mm (f) l3=75 mm
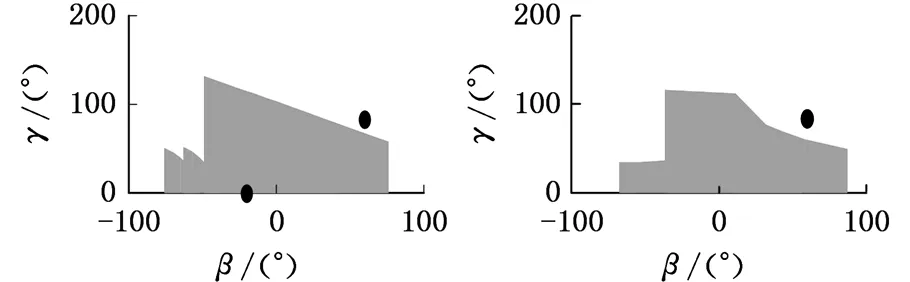
(g) l3=80 mm (h) l3=85 mm
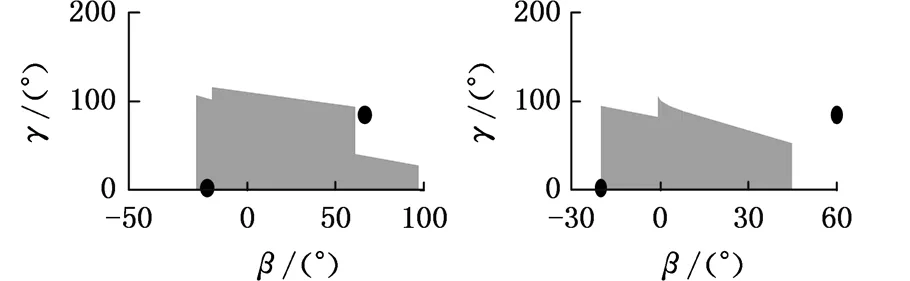
(i) l3=90 mm (j) l3=95 mm
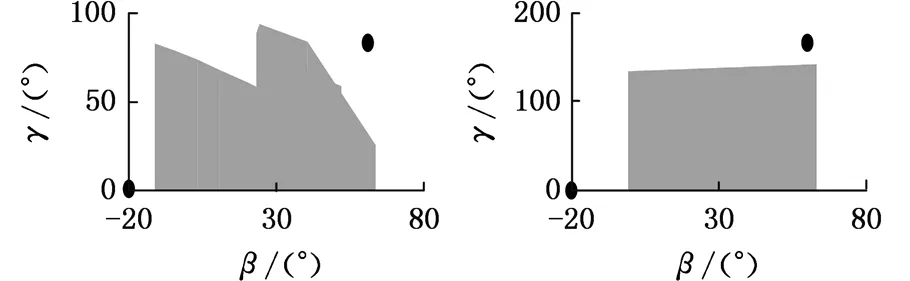
(k) l3=100 mm (l) l3=105 mm图5 不同弧形架长度对应的手指空间状态Fig.5 Different arcs of corresponding length of finger space
(7)
(8)
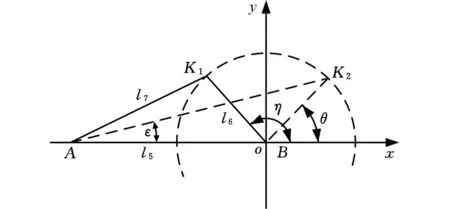
图6 终端机械结构及手指的简化运动模型Fig.6 Simplified motion model of finger and terminal mechanical structure
在△ABK1中,由余弦定理可得
(9)
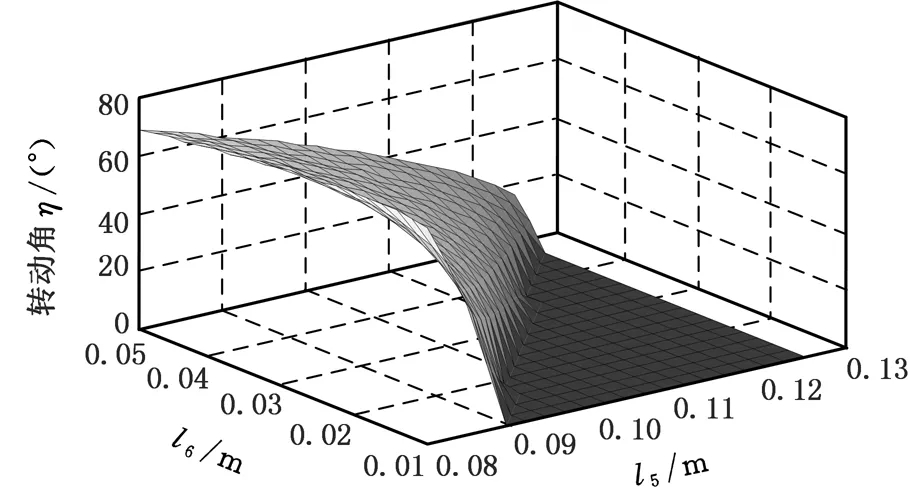
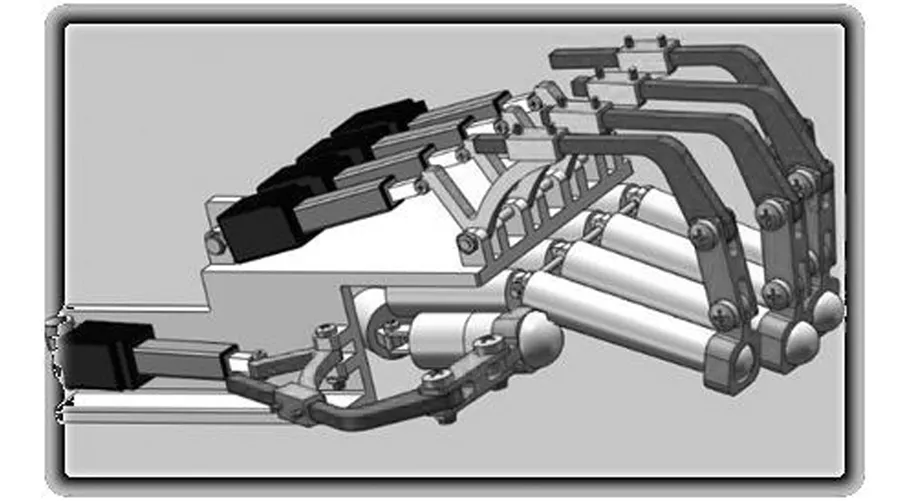
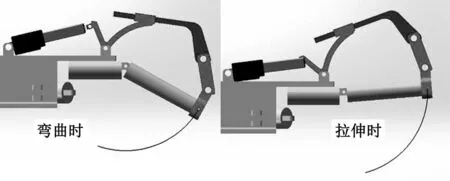
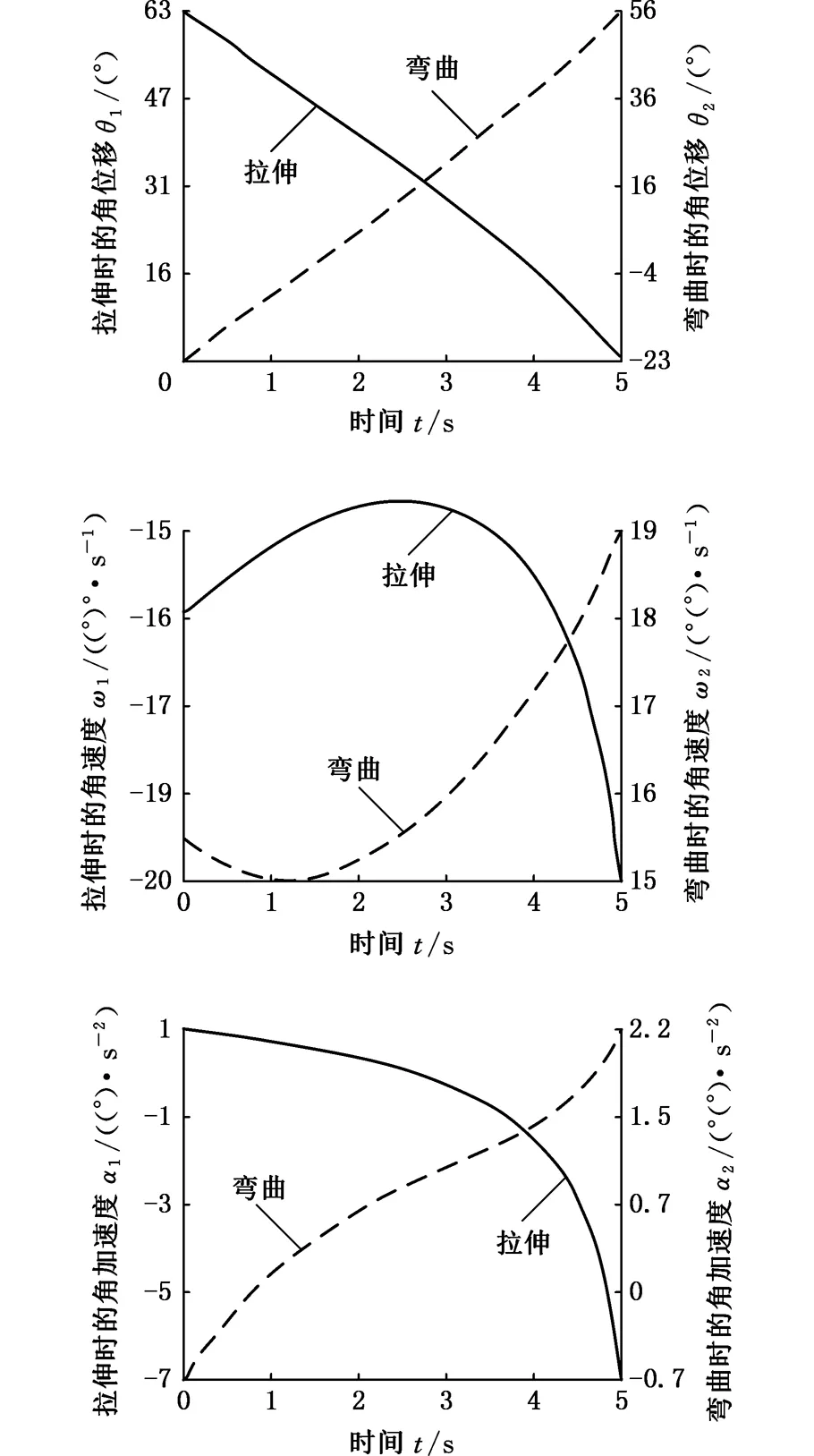
在研究设计该手指康复外骨骼机器人的过程中要充分考虑其可穿戴性,且机械结构应该紧凑,所以应限定l5、l6的尺寸满足:l5min (10) s.t.η-θ≥(η-θ)min 式中,FM为电机的输出力;h为直线AK到原点B的距离,h=l5yK/l7。 2.2.2数值计算 直线电机的位置由l5、l6确定,且必须满足式(6)~式(9)限定的条件。直线电机完全回缩状态下的长度为78 mm,完全伸出时的长度为108 mm。考虑到真实装置的美观性和可穿戴性,实际制作的机械结构尺寸不宜过大,因此限定l5<125 mm,l6<50 mm,η-θ>88°,为了便于计算,在此设定η-θ=90°。FM由电机自身决定,且为定值15 N。利用MATLAB对式(7)~式(9)进行了数值计算,从而得到不同l5、l6组合下直线电机推动弧形架的平均输出转矩和直线电机可推动弧形架转动角度的关系图(图7、图8)。考虑到输出扭矩和电机推动弧形架的转动角要尽可能的大,可得l5、l6的最佳值115 mm和50 mm,此时电机可推动弧形架转动的角度η=180°-30°=150°。 图7 平均输出转矩与l5、l6的变化关系Fig.7 Relationship between average output torque and l5, l6 图8 转动角与l5、l6的变化关系Fig.8 Relationship between angle of rotation and l5, l6 当合理的机械机构尺寸确定后,对原拟定的尺寸进行修改以确定合理的机械构件,利用Solidworks来对手指康复外骨骼机器人进行虚拟装配和运动仿真。得到了图9所示的手指康复外骨骼机器人,该机器人不仅可以以“握手 ”的形式牵拉手指终端,带动手指各个关节完成弯曲和伸展运动,而且可适用于不同长度的手指进行康复活动和锻炼,能够很好地完成对患者手指的被动训练任务。 图9 手指康复外骨骼机器人装置Fig.9 Structure of finger rehabilitation exoskeleton robot 机械运动仿真对后期物理样机制作和控制系统的设计具有极其重要的意义[14],因此,本文采用Solidworks中的Motion工具箱对该机器人带动但手指进行康复训练,进行了运动学仿真,仿真界面及手指末端轨迹如图10所示。 图10 手指末端的运动轨迹Fig.10 Movement trajectory of the end of the finger Motion工具箱的主要仿真参数如下:直线电机速度5 mm/s;仿真时间5 s,仿真帧数100。仿真结果如图 11 所示,其中包含该机器人在带动手指完成弯曲/拉伸动作时,手指的角位移、角速度和角加速度等相关数据。由图 11 可以得到,在设定的运动参数中,机器人带动手指做弯曲运动时,手指末端在yz平面的最大角位移为 79°,最大角速度为20°/s,最大角加速度为 7°/s2;机器人带动手指做拉伸运动时,手指末端在yz平面的最大角位移为 78°,最大角速度为19°/s,最大角加速度为 2.2°/s2。仿真结果表明,该机器人能按照预期给定的参数进行运动。从位移曲线也可以看出,该机器人运动平稳,能带动手指在预期的活动范围内运动,因此可以用于辅助手指损伤患者进行康复训练。 图11 手指末端运动情况Fig.11 The movement of the end of the finger 通过对国内外手指康复外骨骼机器人研究现状的综合分析,设计优化了一种手指康复外骨骼机器人;在对手指康复外骨骼机器人建模的基础上,对其机械系统进行运动学分析,得到了各构件的最佳尺寸;经过运动仿真,得到了机器人的运动轨迹和机器人末端的运动参数曲线。从结果可以看出,该机器人能带动手指能按照一定范围角度进行弯曲/拉伸运动,能够满足手指损伤患者的康复训练,验证了设计的合理性,具有一定的使用价值。 [1] GEZGIN E, CHANG P H, AKHAN A F. Synthesis of a Watt Ⅱ Six-bar Linkage in the Design of a Hand Rehabilitation Robot[J]. Mechanism & Machine Theory, 2016, 104: 177-189. [2] 陈学斌,高海鹏,刘文勇,等.手外骨骼康复技术研究进展[J].中国医疗设备,2016,31(2):86-91. CHEN Xuebin, GAO Haipeng, LIU Wenyong, et al. Research on the Development of Hand Exoskeleton as a Rehabilitation Technology [J]. China Medical Devices, 2016, 31(2): 86-91. [3] 易荣武,王爱民.手指远程康复训练机器人系统设计 [J].电子测量技术,2016,39(9):128-132. YI Rongwu, WANG Aimin. Design of Remote Rehabilitation Training Robotic System for Fingers [J]. Electronic Measurement Technology, 2016, 39(9):128-132. [4] 张帆,郭书祥,魏巍.欠驱动式外骨骼手指康复机器人的设计和仿真 [J].天津理工大学学报,2015,31(2):30-34. ZHANG Fan, GUO Shuxiang, WEI Wei. The Design and Simulation of the under Actuation Exoskeleton Finger Rehabilitation Robot [J]. Journal of Tianjin University of Technology, 2015,31(2):30-34. [5] 杨成阳,尤跃东,赵岩. 手指康复机器人串联弹性驱动器的设计与仿真[J].机械制造,2016,54(7):4-7. YANG Chengyang, YOU Yuedong, ZHAO Yan. Design and Simulation of a Series of Flexible Elastic Actuator for Finger Rehabilitation [J]. Machinery, 2016,54(7):4-7. [6] 李超,袁锐波,丘世因,等.外骨骼康复机械手的结构设计及仿真分析[J].机械与电子,2016,34(2):16-19. LI Chao, YUAN Ruibo, QIU Shiyin, et al. Design and Kinematical Analysis of Exoskeletal Rehabilitation Robot Hand [J]. Machinery & Electronics,2016,34(2):16-19. [7] 郑杨,陈垒,王刚,等. 欠驱动式手指康复训练装置的结构优化设计[J].西安交通大学学报,2008,29(4):151-156. ZHENG Yang, CHEN Lei, WANG Gang, et al. A Structure Optimal Design of Training Devices for the Under-actuated Hand Rehabilitation [J]. Journal of Xi’an Jiaotong University, 2008, 29 (4):151-156. [8] SOEKADAR S R, WITKOWSKI M, VITIELLO N, et al. An EEG/EOG-based Hybrid Brain-neural Computer Interaction(BNCI) System to Control an Exoskeleton for the Paralyzed Hand[J]. Biomedizinische Technik Biomedical Engineering, 2015, 60(3): 199-205. [9] WANG J, LI J, ZHANG Y, et al. Design of an Exoskeleton for Index Finger Rehabilitation[C]//Conf. Proc. IEEE Eng. Med. Biol. Soc.. Minnesota, USA, 2009: 5957-5960. [10] 刘洪山.手创伤康复机械手结构设计与分析[D].哈尔滨:哈尔滨工业大学,2007. LIU Hongshan. Structure Desing and Analysis of Mechanical Hand for Rehabilitation[D]. Harbin: Harbin Institute of Technology, 2007. [11] IQBAL J, TSAGARAKIS N G, FIORILLA A E, et al. A Portable Rehabilitation Device for the Hand.[C]// Conf. Proc. IEEE Eng. Med. Biol. Soc. Engineering in Medicine & Biology Society. Chengdu, 2010: 3694-3697. [12] POLOTTO A, MODULO F, FLUMIAN F, et al. Index Finger Rehabilitation/Assistive Device[C]// The Fourth IEEE RAS/EMBS International Conference on Biomedical Robotics and Biomechatronics. Roma, 2012: 1518-1523. [13] 于美丽. 基于ADAMS外骨骼康复机械手的设计和仿真分析[D]. 青岛:青岛大学,2012:11-12. YU Meili. The Design and Simulation of Exoskeleton Hand Rehabilitation Manipulator Based on ADAMS [D]. Qingdao: Qingdao University, 2012:11-12. [14] 贾先,赵升吨,范淑琴,等. 双动压力机用压边滑块串联四连杆工作机构的优化[J]. 中国机械工程, 2016, 27(9): 1223-1228. JIA Xian, ZHAO Shengdun, FAN Shuqin, et al. Optimization of Pressure Side Slider Series Four-bar Linkage Working Mechanism Used by Double-action Press[J]. China Mechanical Engineering, 2016, 27(9): 1223-1228.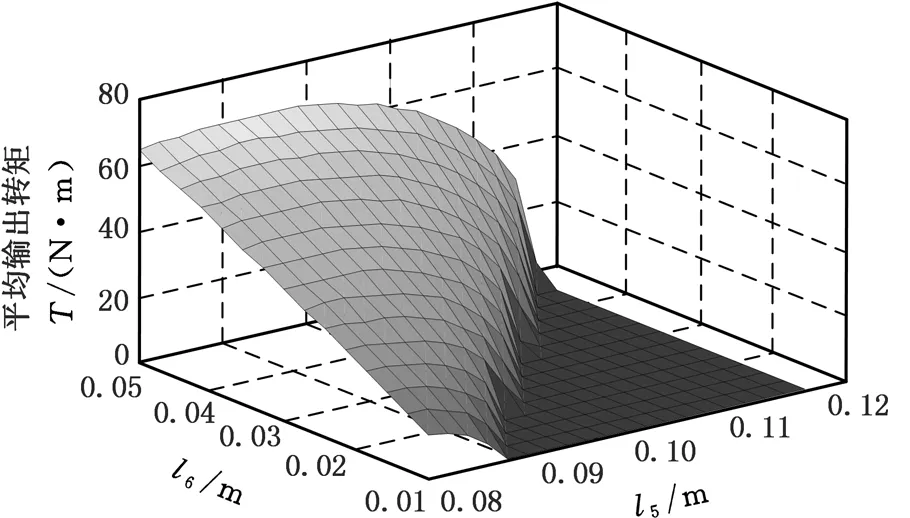
3 模型装配与仿真分析
4 结语

