非圆齿轮-槽轮机构的运动学分析

叶素娣，刘玉婷

(芜湖职业技术学院 电气工程学院，安徽 芜湖 241000)

0 引言

工程中需要这样一种机构，当主动件做连续运动时，从动件做有规律的间歇运动。槽轮机构因其结构简单，工作可靠，传动效率较高，常用作转位分度以及要求单向间歇运动的场合[1]，如自动机床的转位机构，电影放映机中电影胶片间歇移动机构等。

槽轮机构在工作过程中存在柔性冲击，冲击程度与转速、径向槽数相关，当转速增高、槽数减少时，冲击随之加剧。如果用非圆齿轮机构作为其前置机构，改变拨盘的转动规律，就能调和槽轮在运动过程中的冲击现象，从而改善槽轮机构传动的平稳性[2-3]。

1 槽轮机构的运动学建模

外槽轮机构运动简图如图1所示。假设槽轮有z个径向槽，为了避免圆销A在进入和退出径向槽的瞬间发生刚性冲击，径向槽中心线应与圆销进入和退出径向槽的瞬时速度方向处于同一直线上，即AO1⊥AO2,作AB⊥O1O2。

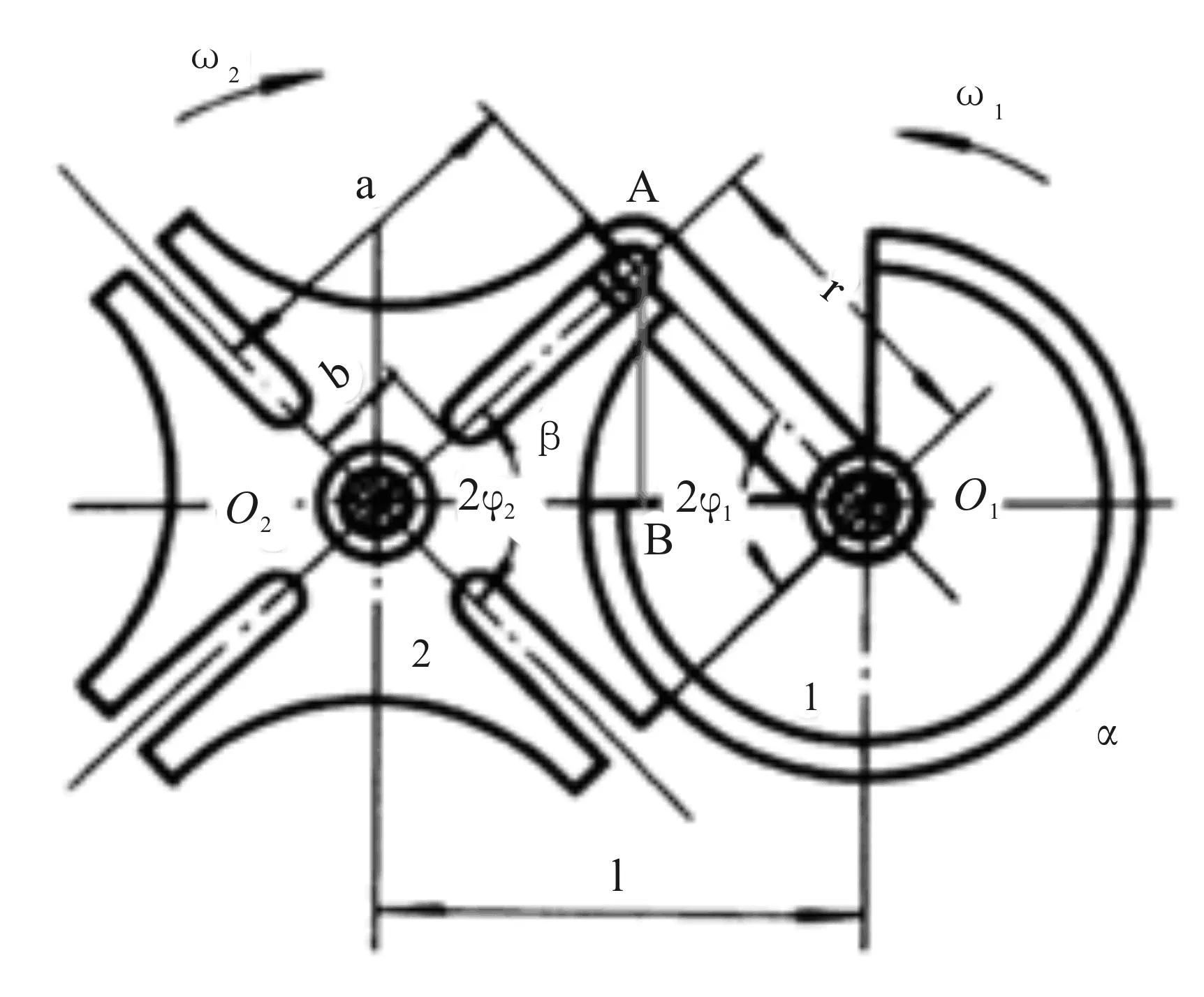
图1 外槽轮机构运动简图

当拨盘逆时针转过2φ1时，槽轮顺时针转过2φ2，故在ΔABO2中有：

(1)

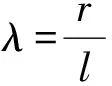
式中，r为拨盘的半径，l为拨盘和槽轮的中心距。

得到：

(2)

对(2)式求导，得到槽轮角速度ω2：

(3)

式中，ω1表示拨盘的转速，ω2表示槽轮的转速。

以拨盘转角φ1为横坐标，槽轮相对角速度ω2/ω1为纵坐标，取z=4，z=6，z=8，槽轮相对角速度变化规律如图2所示。

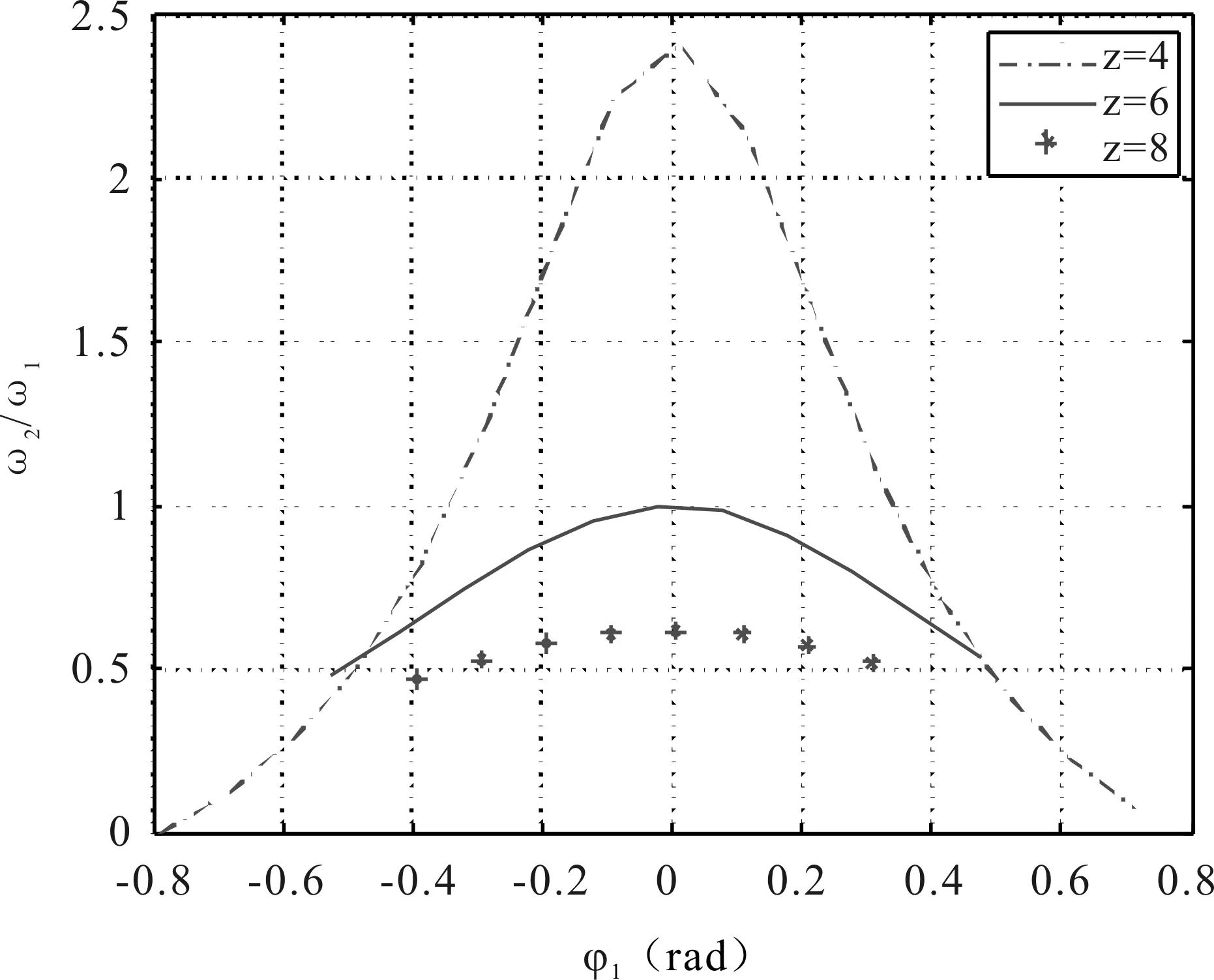
图2 槽轮相对角速度变化规律

对(3)式求导，得到槽轮角加速度α2：

(4)

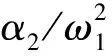
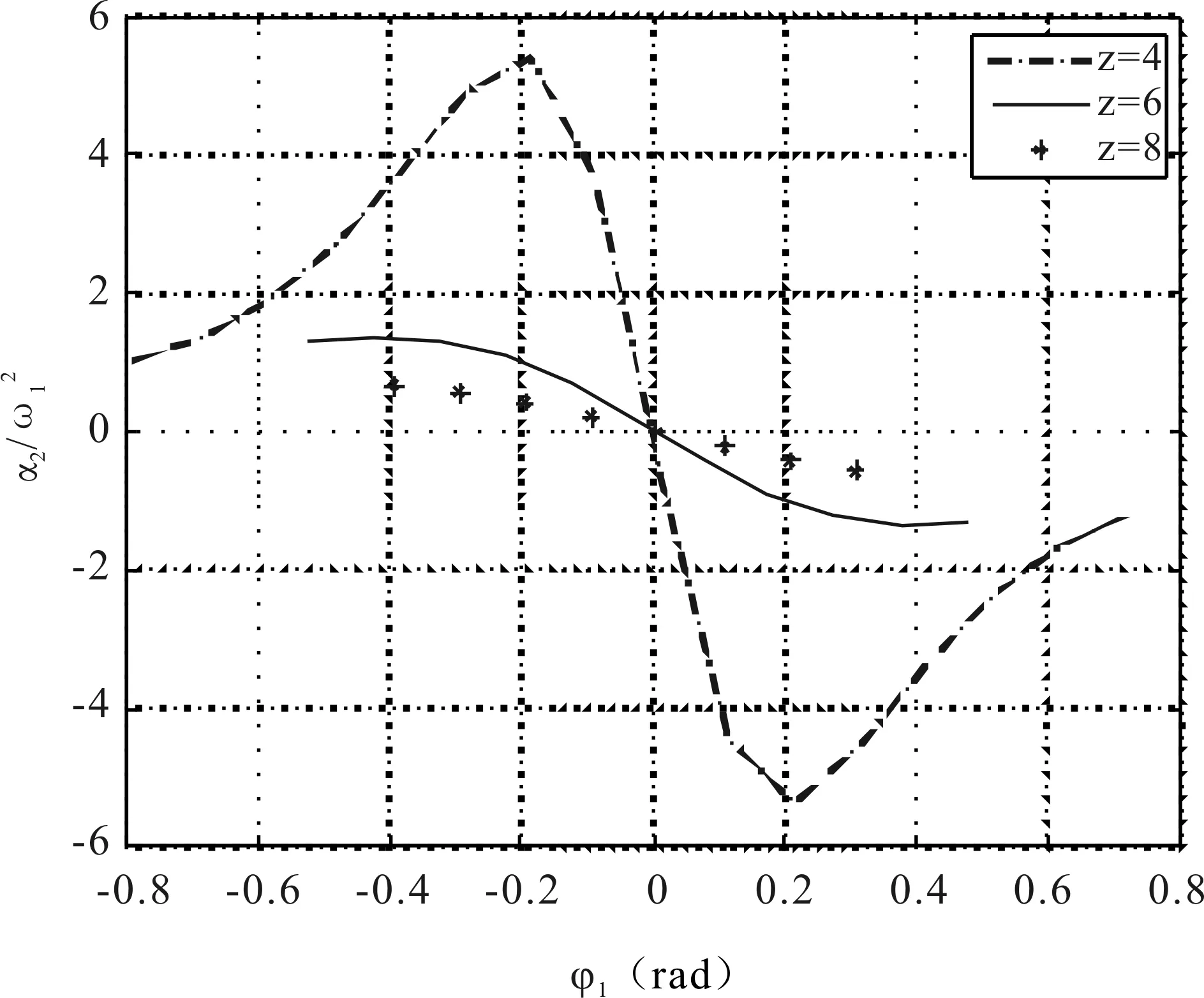
图3 槽轮的相对角加速度变化规律

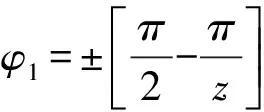
2 具体应用中的槽轮机构分析

槽轮的运动特性参数对槽轮机构的运动平稳性有很大的影响，例如在电影放映机电影胶片间歇移动机构中，胶片移动速度变化越小，电影放映质量越好，而其加速度的大小范围直接反映速度的波动范围，所以须在工作进程中减小加速度的最值，缩小速度的波动范围，使速度尽可能平稳。基于此，需要对槽轮的运动特性参数进行优化。

由式(1)至式(4)可知，在输入角位移值一定的情况下，以拨盘半径、径向槽数和安装中心距为设计变量，以槽轮输出速度来建立目标函数进行优化[4]，经过优化设计并仿真，采用槽轮机构能满足电影放映机的运动要求。

而当槽轮机构的各个参数值一定时，通过设定不同的输入角位移值，也会影响输出的速度变化，由此也能设计出满足应用要求的槽轮机构。

考虑到在实际工程应用中，对槽轮机构的结构参数有一定的限制和要求，因此通过控制电机的输出速度来改变输入到槽轮机构的角位移值，从而使槽轮机构输出速度变化更具有灵活性。

若使电机的输出(拨盘的输入)运动规律为：

φ1=2arccot[2.78cot(0.5x)]

(5)

式中，x为虚拟轴角位移。

此时可得拨盘角速度ω1：

(6)

将式(5)和式(6)代入式(3)、式(4)中，得到槽轮机构在变速输入时槽轮的角速度及相对角加速度变化规律分别如图4和图5。

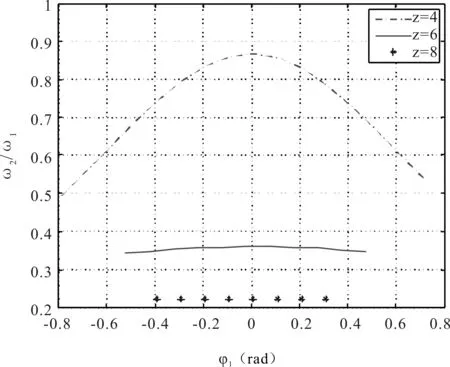
图4 变速输入时槽轮的角速度变化规律

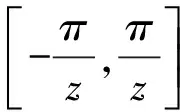
图5 变速输入时槽轮的相对角加速度变化规律

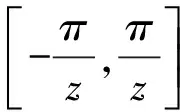
3 非圆齿轮-槽轮机构串联运动分析

考虑到电机按φ1=2arccot[2.78cot(0.5x)]变速要求会增大采购成本，故采用由匀速电机通过驱动一对非圆齿轮，再现式(5)运动规律来获得变速输出作为槽轮机构的输入。非圆齿轮和槽轮机构的串联机构运动简图如图6所示。

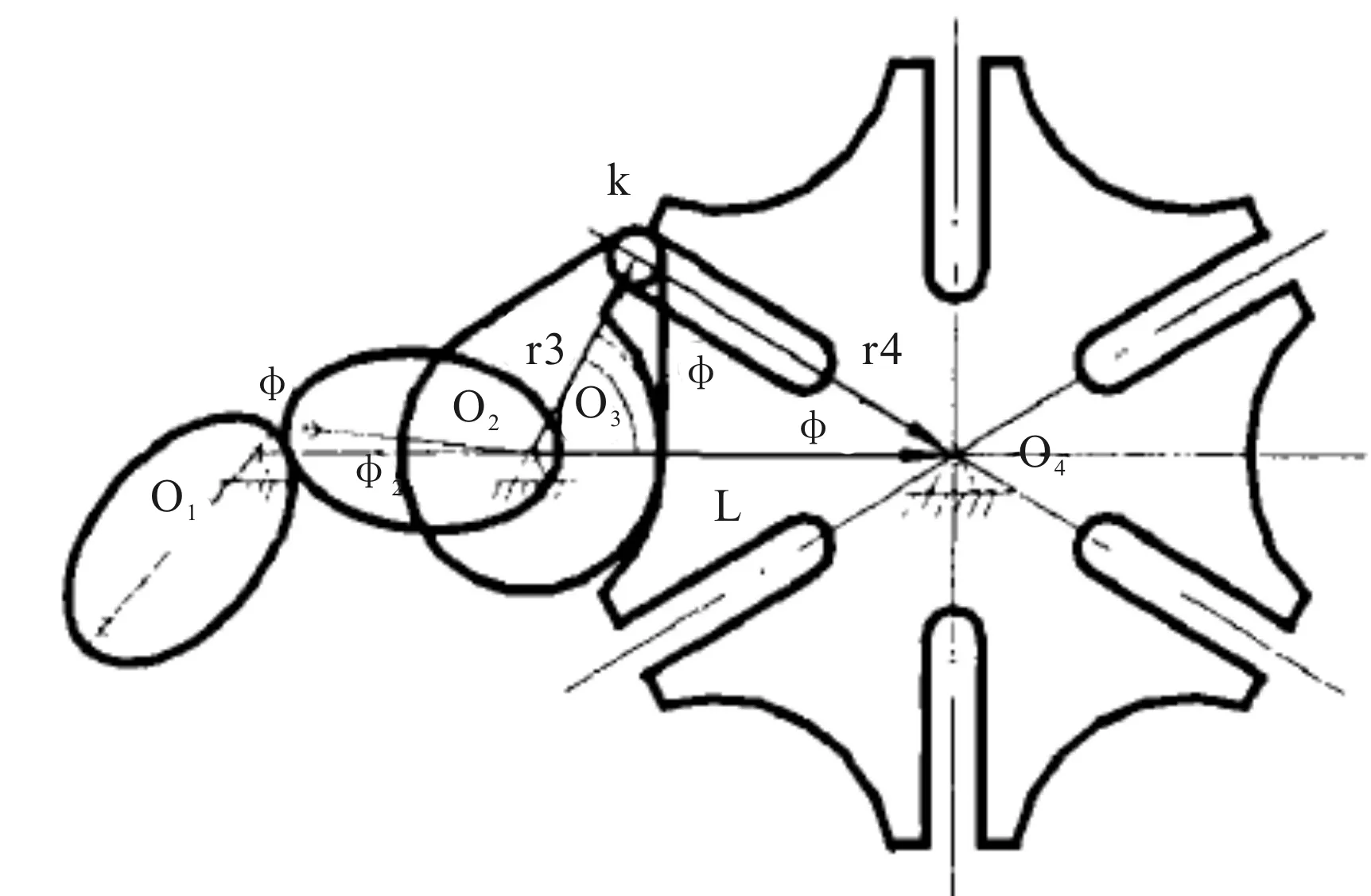
图6 非圆齿轮和槽轮机构的串联机构简图

当主动椭圆齿轮1匀速转动时，因从动椭圆齿轮2与拨盘3同轴安装[5-6]，故而一起作变速转动，实现槽轮在变速输入时的间歇运动。即：

φ2=2arccot[2.78cot(0.5φ1)]

(7)

满足式(7)的非圆齿轮的传动比：

(8)

而非圆齿轮的瞬时传动比又可表示为：

(9)

从而得到：

(10)

假设中心距a=50mm，节曲线r1、r2关于转角φ1的函数用matlab编程画出其图形，得出一对节曲线关于转角函数变化图形如图7所示。

如图7所示，这对非圆齿轮与槽轮机构按图6所示串联运动，就能使槽轮机构实现图4、图5所示的运动规律。

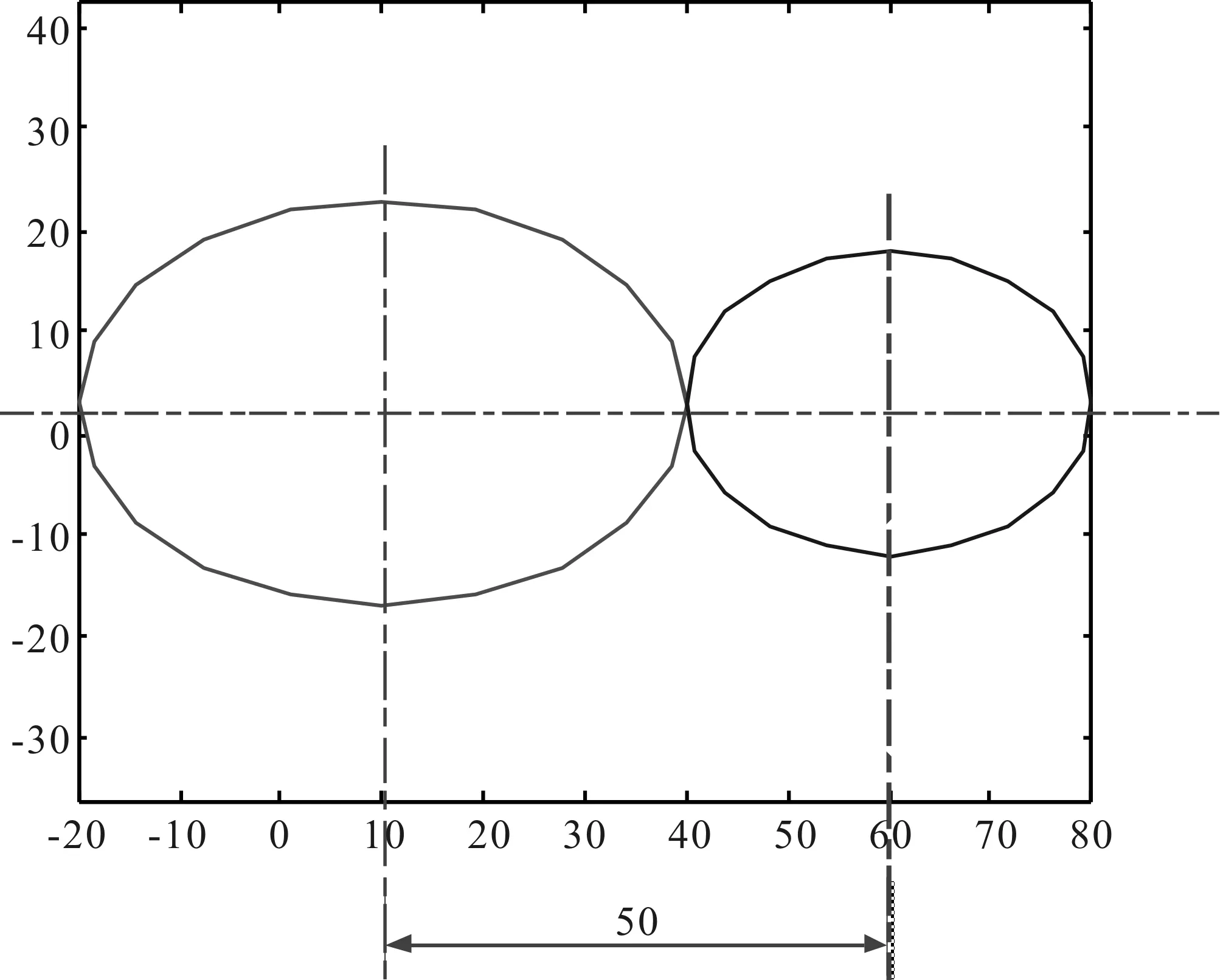
图7 一对节曲线关于转角函数变化图形

4 结语

槽轮机构在具体工程应用中，要求传动平稳，冲击小。通过建模仿真分析可知，槽轮机构中径向槽数越多，槽轮机构柔性冲击越小。在径向槽数、槽轮半径以及安装中心距优化设计[7]的前提下，既可以通过电机单向变速驱动槽轮机构改善槽轮机构运动平稳性，也可以通过匀速电机驱动非圆齿轮副与槽轮机构串联组合的方式实现槽轮机构在满足运动平稳时实现其功能，这一方法适合于自动机床的转位机构和电影放映机的胶片间歇移动机构。可以选用不同工程应用中的单向变速运动函数，通过再现此函数来反求非圆齿轮副[8],从而使槽轮机构的应用更具广泛性。

[1] 顾淑华，耿谦.椭圆齿轮在槽轮机构中的设计应用[J].机械设计,2009,26(8):53-56.

[2] 蒋淼,陈建能,赵匀.椭圆齿轮-曲柄滑块机构运动特性分析[J].浙江理工大学学报,2009,26(2):256-260.

[3] 陈建能,赵雄,徐宾,等.椭圆齿轮-曲柄摇杆引纬机构的运动学建模与特性分析[J].中国机械工程,2007,18(19):2294-2298.

[4] 白云娇,谷伟平.基于精确目标罚参数的遗传算法[J].重庆工商大学学报(自然科学版),2016,33(2):30-33.

[5] 叶素娣,徐敬华.卵形齿轮-槽轮串联机构的运动学建模及分析[J].西安文理学院学报(自然科学版),2017，20(3):28-32.

[6] 叶素娣,徐敬华.三阶非圆齿轮泵的流量脉动及可滚齿性研究[J].西安航空学院学报,2017,35(3):37-42.

[7] 章盛,韩超.一种优化的图像拼接方法[J].重庆工商大学学报(自然科学版),2015，32(12)：8-13.

[8] 蔡军.非圆齿轮-摆动导杆机构的应用与运动学分析[J].机械传动,2017,14(2):139-142.