高功率密度电机控制器的IGBT模块损耗及结温计算

丁 杰，张 平

（1.湘潭大学土木工程与力学学院，湘潭411105；2.株洲南车时代电气股份有限公司技术中心，株洲，412001）

随着能源与环境问题的日益凸显，传统燃油汽车向电动汽车转变已经越来越紧迫。发展电动汽车必须解决电池、电力驱动及其控制、整车轻量化、能量管理等关键技术，因此，结构紧凑的高功率密度电机控制器是电动汽车的关键部件，而IGBT模块是电机控制器中最为核心的器件[1]。由于IGBT模块在工作过程中产生的损耗不仅影响电机控制器的工作效率，还会导致结温上升，对系统的可靠性产生重要影响。

为设计可靠性高的高功率密度电机控制器，计算IGBT模块的损耗和结温是一项至关重要的工作。国内外学者已较为深入研究了IGBT模块的损耗计算方法，提出的损耗计算模型主要有基于物理结构和基于数学方法两大类[2,3]。基于物理结构的IGBT损耗模型采用电容、电感、电阻、电压源和电流源等元件模拟IGBT模块特性，利用电压、电流波形得到IGBT模块的损耗，目前已有几种较为成熟的物理仿真模型应用于Saber、Spice等软件。该方法需要熟悉IGBT模块的内部结构、物理等效参数和微观工作过程，然而获取等效参数的难度很大，因此该方法较少应用于工程领域[4]。基于数学方法的IGBT模块损耗模型以大量试验测试数据为基础，用数学函数（如指数、线性、多项式、三角形、数据手册插值等）表示损耗与各影响因素之间的数量关系，从而快速地计算出工作条件下的损耗[5]。Infineon公司开发的IPOSIM软件基于数据手册进行损耗计算，提供的表格中包含了数百种IGBT模块的典型参数，具有功能强大、使用方便等优点[6]。

在设计一款电动汽车用高功率密度电机控制器时，受空间体积限制，选择了一个集成六单元的FS800R07A2E3型IGBT模块直接构成三相逆变电路，输出功率可达80 kW。由于IPOSIM软件没有提供该型号IGBT模块的损耗与结温计算功能，且数据手册中仅提供了采用25℃50%水/50%乙二醇混合物进行冷却的热阻曲线，电机控制器实际使用时的冷却水温度可达65℃，此时的冷却水热物性参数已有较大变化，直接使用数据手册中的参数进行计算必将产生较大的误差。

鉴于此，本文分析了利用数据手册计算IGBT模块损耗和结温的方法，通过计算流体动力学CFD（computational fluid dynamics）软件FLUENT得到实际冷却水温度下的热阻值，解决了数据手册中热性能数据不完善的问题，基于Matlab开发了损耗及结温计算程序，可以计算出不同工况下的损耗和结温等重要参数。

1 高功率密度电机控制器的结构

某电动汽车用高功率密度电机控制器如图1所示，其主要由机壳、外盖、FS800R07A2E3型IGBT模块、控制板、接线座、水管等组成。结构整体外形如图1（a）所示，IGBT模块如由图1（b）所示，可以看出IGBT模块底板上有662个叉排的翅柱，与机壳一起形成水冷散热器的结构，用于解决传统IGBT模块安装在散热器上存在较大接触热阻的问题。

图1 高功率密度电机控制器的结构Fig.1 Structure of high power density motor controller

2 基于数据手册的损耗计算

IGBT模块包含IGBT芯片和反并联的续流二极管芯片。IGBT或二极管开通动作结束至关断动作开始前，芯片处于饱和导通状态而产生导通损耗，其中芯片饱和导通压降与芯片流过的电流及结温有关，而与直流母线电压无关。IGBT或二极管在门极电压的控制下，由截止转换为导通或相反的过程中，电压和电流存在明显的交叉重合区，会产生开关损耗。

IGBT和二极管的损耗受直流母线电压、负载电流、芯片结温、门极驱动电压、门极驱动电阻等因素的影响。实际驱动电路通常采用与数据手册测试电路一样的门极驱动电压，其影响详见数据手册。然而直流母线电压、负载电流和芯片结温与具体的应用条件有关，门极驱动电阻值与具体的驱动设计有关，因此，计算IGBT模块损耗时必须考虑这4个因素的影响。

2.1 IGBT的导通损耗

FS800R07A2E3型IGBT模块的数据手册给出了特定结温（25℃、125℃和150℃）下IGBT芯片导通电压Vce与电流Ic之间的输出特性曲线 （见图2），其中的门极驱动电压为15 V。为简化计算，以图2中结温Tj为125℃的曲线为例，通过1号、2号2点的IGBT导通电压与电流进行线性化处理，即

式中：VT0为IGBT门槛电压；Rce为IGBT通态等效电阻。由图2及式（1）可知：Tj=125℃时，VT0=0.8 V，Rce=1.012 mΩ。

图2 Tj=125℃时输出特性的线性插值Fig.2 Linear interpolation of output characteristics at Tjis 125℃

任意结温Tj的导通压降 Vce_Tj可根据图 2中Tj=25℃和Tj=125℃的曲线线性插值计算求得，即

任意结温Tj的IGBT导通损耗瞬时功率为

2.2 IGBT的开关损耗

IGBT开关过程中电压与电流的变化特点复杂，因此，IGBT的开关损耗大多利用数据手册中提供的开关损耗试验测试数据，而非电压乘以电流的方式。数据手册给出了IGBT芯片在直流母线电压为300 V、门极驱动电压为±15 V、门极开通电阻RGon为1.8 Ω、门极关断电阻RGoff为0.75 Ω时，单脉冲开通能耗与关断能耗随集电极电流变化的曲线，见图3。

将已结束项目任务数据中未完成的任务提取出来，再次导入无忧地图并呈现在百度地图上。按照划分的各价格区段将不同定价区间的热量图分别呈现出来研究:

采用线性插值可得到开通能耗Eon和关断能耗Eoff与集电极电流之间的关系，即

图3 Tj=125℃时IGBT开关能耗的线性插值Fig.3 Linear interpolation of IGBT switching energy losses at Tjis 125℃

由图3可知：Tj=125℃时，Eon1=2.381 mJ，Eon2= 15.714 mJ，Eoff1=1.333 mJ，Eoff2=36.189 mJ。

为考虑实际驱动电路门极电阻的影响，可在数据手册中开关能耗随门极驱动电阻的变化曲线查出实际门极电阻对应的开通能耗Eon（RG_real）、关断能耗Eoff（RG_real）以及测试电路门极电阻对应的开通能耗 Eon（RG_data）、关断能耗 Eoff（RG_data）进行修正。 例如：RG_data=1.8 Ω，RG_real=6.5 Ω，Tj=125℃时，通过数据手册中的曲线可知Eon（RG_data）=10.526 mJ，Eoff（RG_data）=27.368 mJ，Eon（RG_real）=52.631 mJ，Eoff（RG_real）=43.789 mJ。为考虑实际直流母线工作电压的影响，可分别采用IGBT开通、关断时刻的实际直流母线电压Vdc_on_real、Vdc_off_real除以测试电压 Vdc_data得到的商进行修正。则式（4）修正为

任意结温Tj下的开通能耗Eon_Tj和关断能耗Eoff_Tj可用图3给出的结温125℃下的开通能耗Eon_Tj125、关断能耗Eoff_Tj125以及150℃下的开通能耗Eon_Tj150、关断能耗Eoff_Tj150进行线性插值，即

2.3 二极管的导通损耗

二极管导通损耗计算方式与IGBT导通损耗类似。首先对图4所示的二极管正向特性曲线进行线性化处理，然后通过Tj=25℃和Tj=125℃的曲线线性插值得到任意结温Tj的导通压降值VF_Tj，最后由VF_Tj与正向导通电流IF相乘得到二极管导通损耗瞬时功率。

式中：VF0为二极管门槛电压；RF为二极管通态等效电阻。由图4及式（7）可知：Tj=125℃时，VF0=0.983 V，RF=0.637 mΩ。

图4 Tj=125℃时正向特性的线性插值Fig.4 Linear interpolation of forward characteristics at Tjis 125℃

2.4 二极管的反向恢复损耗

数据手册中二极管芯片在母线电压为300 V、门极开通电阻为1.8 Ω时单脉冲反向恢复能耗随正向导通电流变化的曲线，见图5。反向恢复能耗与电流之间的关系可表示为

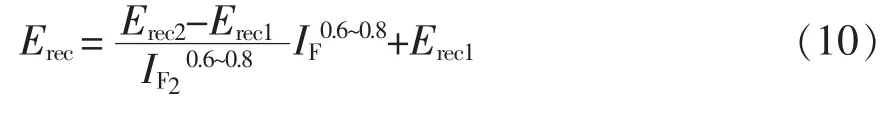
图5 二极管反向恢复能耗随电流变化曲线Fig.5 Curves of reverse recovery energy loss with current changes of diode

为考虑实际驱动电路门极电阻值的影响，可利用数据手册提供的反向恢复能耗随门极开通电阻变化的曲线中查出实际门极开通电阻对应的能耗值Erec（RG_real）除以测试电路门极开通电阻对应的能耗值Erec（RG_data）进行修正。例如：RG_data=1.8 Ω，RG_real= 6.5 Ω，Tj=125℃时，通过数据手册中的曲线可知Erec-（RG_data）=11.162 mJ，Erec（RG_real）=5.096 mJ。为考虑实际工作电压Vdc_rec_real的影响，可采用 Vdc_rec_real除以测试电压Vdc_data得到的商进行修正。式（10）修正为

任意结温下的二极管反向恢复能耗可利用图5中结温125℃、150℃下的反向恢复能耗Erec_Tj125、Erec_Tj150进行插值处理，即

2.5 逆变器持续工作的损耗

工程应用需要计算IGBT模块某一时刻的损耗，也需要计算IGBT模块持续工作的损耗。开关频率fsw影响IGBT的开关损耗和二极管的反向恢复损耗，占空比影响IGBT和二极管的导通损耗。计算各种情况下的持续工作损耗时，可先对IGBT工作的每个脉冲计算IGBT导通能耗Econd_T_i、开通能耗Eon_i、关断能耗 Eoff_i和二极管导通能耗Econd_D_i、反向恢复能耗Erec_i，再累加得到N个脉冲下的IGBT总能耗Etot_T和二极管总能耗Etot_D，或得到该时间段ttot内的IGBT损耗平均功率Ptot_T_av和二极管损耗平均功率 Ptot_D_av。 计算公式为

3 基于等效热路模型的结温计算

3.1 稳态温度计算

IGBT和二极管芯片工作产生的热量会导致芯片结温上升，器件内部材料的热容特性和导热性能会影响结温上升的速率和幅值。FS800R07A2E3型IGBT模块中集成了6个单元，每个单元中包含距离较近的IGBT和二极管芯片，属于复杂的三维结构问题。为简化温度计算，数据手册假设每个芯片完全独立，即单个芯片产生的热量不会对其他芯片的温度产生影响，从而得到一维的IGBT模块散热模型，如图6所示。芯片通过焊料焊接在敷铜陶瓷衬板上，衬板再通过焊料焊接在铜基板上，铜基板底部有许多翅柱用于强化冷却水的散热，芯片产生的热量主要通过下方的多层结构传递到冷却水中。

图6 IGBT模块散热模型Fig.6 Heat dissipation model of IGBT module

稳定状态下的芯片结温Tj可根据芯片损耗平均功率Pav、芯片至冷却水的热阻Rth_jf和冷却水温度Tf计算，即

图 7是 FS800R07A2E3型 IGBT模块采用25℃50%水/50%乙二醇混合物进行冷却，通过改变入口流量得到的IGBT芯片、二极管芯片的热阻曲线和压降曲线。入口流量为10 dm3/min时，IGBT芯片至冷却水的热阻为0.1 K/W，二极管芯片至冷却水的热阻为0.14 K/W，冷却水通过IGBT模块的压降为10 kPa。

3.2 瞬态温度计算

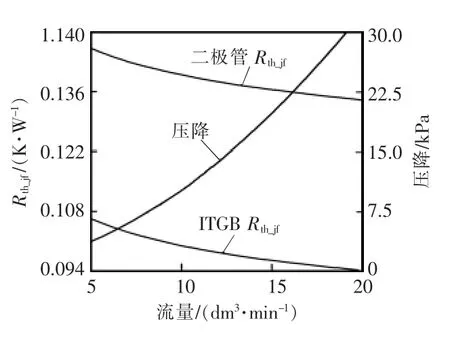
图7 热阻与压降曲线Fig.7 Curves of thermal impedance vs pressure drop

为计算瞬态温度，可以使用连续网络（Cauer）和局部网络（Foster）两种不同的等效热路模型。Cauer模型可以针对模块的每一层材料使用相应独立的热阻热容单元而获得其温度，反映器件内部真实的热量传导过程。Foster模型使用虚拟的节点，其热阻热容参数不再与器件内部各层材料相对应。由于Foster模型的参数比Cauer模型更容易通过试验测量得到，故在数据手册中得到应用。

Foster模型包含n层材料，已知每层的热阻ri、热容单元ci，传热时间常数τi=rici，则瞬态热阻抗为

表1是FS800R07A2E3型IGBT模块中IGBT和二极管芯片的Foster模型参数。利用式（15）和表1的参数可以得到如图8所示的IGBT和二极管芯片瞬态热阻抗曲线。

不同时刻的芯片结温Tj（t）可根据芯片损耗功率P（t）、瞬态热阻抗和冷却水温度Tf（t）计算，即

由于损耗与结温有关，结温又直接受损耗的影响，利用上述公式时需要经过迭代计算才能得到相应的结果。

表1 Foster模型参数Tab.1 Parameters of Foster model

图8 瞬态热阻抗曲线Fig.8 Curves of transient thermal impedance

4 基于CFD计算的参数修正

数据手册中仅提供了采用25℃50%水/50%乙二醇混合物进行冷却的热阻抗曲线，电机控制器实际使用时的冷却水温度可达65℃。50%水/50%乙二醇混合物在25℃的密度为1 071.8 kg/m3、导热系数为0.289 W/m·K-1、比热容为3.130 kJ/kg·K-1、动力粘度为4.015×10-3kg/m·s-1，在65℃的密度为1 043.0 kg/ m3、导热系数为0.378 W/m·K-1、比热容为3.345 kJ/ kg·K-1、动力粘度为1.525×10-3kg/（m·s-1），说明温度对冷却水的热物理参数有较大的影响[7]，因此，针对实际的使用条件，直接采用数据手册中的参数进行计算必将产生较大的误差。

为比较数据手册中提供的热阻值与CFD计算结果的差异，利用HyperMesh软件建立了高精度的网格模型，冷却水采用25℃50%水/50%乙二醇混合物，入口流量为10 dm3/min，设置IGBT芯片总损耗为600 W，二极管芯片总损耗为0，即一个单元的IGBT芯片损耗为100 W，采用FLUENT软件的标准k-ε模型可得到如图9所示的温度场分布。图9（a）表示高功率密度电机控制器整体的温度场分布，最高温度36.93℃出现电机控制器的内部。图9（b）表示IGBT模块的温度场分布，可看出IGBT芯片上的最高温度为36.93℃，相对于入口冷却水温度而言，温升为11.93 K，对应的IGBT芯片至冷却水的热阻为0.119 K/W，高于数据手册的热阻数据（0.1 K/W）。热阻数据有差异的原因主要有：冷却水流经IGBT模块时会有所升温，处于冷却水下游的芯片温度要高于上游；制作的机壳和器件厂商测试条件有差异，对内部的冷却水流动情况有一定影响；6组芯片的位置相邻，对温度存在一定的相互影响。由CFD计算可知冷却水在槽道中的压降为17.87 kPa，远高于数据手册的压降数据（10 kPa），这是由于电机控制器上包含了2个90°弯管用于冷却水的流入与流出，会产生较大的局部压力损失。

图9 IGBT芯片发热时的温度场分布Fig.9 Temperature field distribution under IGBT chip heating

将二极管芯片总损耗改为600 W，而二极管芯片总损耗设置为0，即一个单元的二极管芯片损耗为100 W，由CFD计算可以得到二极管芯片上的最高温度为41.26℃，温升为16.26 K，对应的二极管芯片至冷却水的热阻为0.163 K/W，高于数据手册的热阻数据 （0.14 K/W）。将冷却水温度改为65℃，其余条件相同，可以计算出IGBT、二极管芯片至冷却水的热阻分别为0.113 K/W和0.154 K/W，较冷却水温度25℃时的热阻值有所下降。因冷却水动力粘度的大幅度降低，冷却水通过电机控制器的压降减小为7.17 kPa。

5 损耗及结温计算程序开发与应用

基于前面所述的损耗、结温计算方法和数据手册中的参数，利用Matlab软件的M语言开发了损耗及结温计算程序，可以计算二电平三相桥式逆变器不同工况下的损耗和结温等。需要输入的参数主要有：电机线电压、线电流、基波频率、功率因数、开关频率和冷却水温度等。

输入电机线电压259.8 V、线电流400 A、基波频率50 Hz、功率因数0.88、开关频率8 kHz、冷却水温度65℃，通过程序可以计算出一个单元的IGBT芯片和二极管芯片在单个周期内平均的损耗，其中IGBT芯片的通态损耗为194.0 W、开通损耗为201.7 W、关断损耗为168.8 W、总损耗为564.5 W，二极管芯片的通态损耗为27.0 W、反向恢复损耗为37.8 W、总损耗为64.8 W。还可以计算出IGBT和二极管的周期平均结温分别为128.79℃和74.98℃。

基于同样的输入参数，利用程序可以计算出IGBT模块持续工作时一个单元的IGBT芯片和二极管芯片能量耗散及结温周期变化曲线，如图10所示。由图10可以看出一个开关周期内，IGBT和二极管芯片的能量耗散随着相位角改变而发生变化，相应的结温在其周期平均结温的附近波动。

图10 能量耗散与结温周期变化曲线Fig.10 Curves of energy dissipation vs junction temperature periodic variation

利用程序还可以计算复杂工况下的损耗及结温。图11是电动汽车在某线路条件下的车速曲线，可以看出电动汽车在运行过程中频繁出现起步、加速、匀速、减速、停车等工作模式。借助车辆动力学和电机拖动的知识以及电动汽车仿真软件Advisor进行性能仿真，可以得到电机控制器在不同时刻的电压、电流、输出频率、功率因数等电气参数，将这些电气参数提供给损耗及结温计算程序可以得到IGBT模块一个单元的芯片损耗和结温曲线 （见图12）。由图12（a）可以看出不同工作模式下的损耗会产生明显的差异，根据式（16）可知不同时刻的芯片结温取决于芯片损耗功率、瞬态热阻抗和冷却水温度，因IGBT模块的热容较小且冷却水温度恒定，因此，图12（b）表示的芯片结温变化规律与损耗差异很小。由于图6所示的IGBT模块散热模型中，并未体现同一模块中不同芯片的热耦合效应，导致IGBT芯片的发热未对二极管芯片结温产生影响，反之亦然。基于数据手册的IGBT模块散热模型计算结温时，还需要考虑一定的温度裕度，才能保证IGBT模块的安全可靠运行。

图11 车速曲线Fig.11 Curve of vehicle speed

图12 基于线路条件的损耗和结温变化曲线Fig.12 Curves of loss and junction temperature based on line condition

为解决热耦合效应的问题，损耗计算部分仍可采用前面所述方法，结温计算部分可以先通过CFD计算得到精细网格的对流换热系数分布，然后将对流换热系数分布映射在粗糙网格的有限元模型中，再提取有限元模型的热阻矩阵和热容矩阵，最后通过模型降阶法缩聚矩阵的自由度，从而实现瞬态温度场的快速准确计算[8,9]。借助开发的程序，将损耗计算部分与瞬态温度场快速计算部分进行迭代，可更加准确地得到复杂工况下的损耗和结温，这些内容将在后续工作中开展。

6 结语

本文介绍了高功率密度电机控制器中FS800R 07A2E3型IGBT模块损耗和结温计算的方法，并提出了利用CFD计算完善数据手册热性能参数的方法，开发的程序不仅可以计算IGBT模块持续工作时一个开关周期内能量耗散和结温随相位角变化的结果，还可以基于线路条件计算不同时刻的损耗和结温，具有简单易用且适合工程应用的特点。针对现有简化的散热模型中未体现同一模块中不同芯片的热耦合效应，不能考虑IGBT和二极管芯片彼此之间的发热与温升的相互影响，后续将利用开发的程序与瞬态温度场开展联合计算，从而更加准确地计算损耗和结温，为IGBT模块的疲劳寿命预估奠定基础。

[1]陈清泉.现代电动汽车技术[M].北京：北京理工大学出版社,2002.

[2]熊妍,沈燕群,江剑,等.IGBT损耗计算和损耗模型研究[J].电源技术应用,2006,9（5）：55-60.

Xiong Yan,Shen Yanqun,Jiang Jian,et al.Study on loss calculation and model for IGBT[J].Power Supply Technologies and Applications,2006,9（5）：55-60（in Chinese）.

[3]景巍.大功率三电平变频器功率器件损耗研究[D].徐州：中国矿业大学,2011.

Jing Wei.Study on power device losses of high-power three-level converter[D].Xuzhou：China University of Mining and Technology,2011（in Chinese）.

[4]Kang Wangying,Ahn H,Nokali M A E.A parameter extraction algorithm for an IGBT behavioral model[J].IEEE Transactions on Power Electronics,2004,19（6）：1365-1371.

[5]Xu Dewei,Lu Huawei,Huang Lipei,et al.Power loss and junction temperature analysis of power semiconductor devices[J].IEEE Transactions on Inductry Applications, 2002,38（5）：1426-1431.

[6]丁杰,唐玉兔,忻力.一种改进的二电平IGBT变频器损耗计算方法[J].大功率变流技术,2013（4）：18-21.

Ding Jie,Tang Yutu,Xin Li.An improved method of loss calculation for two-level IGBT converters[J].High Power Converter Technology,2013（4）：18-21（in Chinese）.

[7]丁杰,张平.翅柱式IGBT水冷散热器的热仿真与实验[J].电源学报,2015,13（4）：70-76.

Ding Jie,Zhang Ping.Thermal analysis and test of IGBT water-cooling radiator with pin-fins[J].Journal of Power Supply,2015,13（4）：70-76（in Chinese）.

[8]丁杰,唐玉兔.模型降阶方法在瞬态热仿真中的应用[J].机车电传动,2014（5）：51-55.

Ding Jie,Tang Yutu.Application research of model order reduction method in transient thermal analysis[J].Electric Drive for Locomotives,2014（5）：51-55（in Chinese）.

[9]丁杰,唐玉兔,忻力,等.输出频率对IGBT元件结温波动的影响[J].电气传动,2014,44（6）：76-80.

Ding Jie,Tang Yutu,Xin Li,et al.Effects of output frequency on junction temperature ripple for IGBT module[J]. Electric Drive,2014,44（6）：76-80.