基于Petri网模型的泛化度计算方法

，

(山东科技大学 计算机科学与工程学院，山东 青岛 266590)

过程挖掘[1-5]的目标是通过挖掘算法从给定的事件日志中挖掘出拟合、泛化、精确、简洁的过程模型。由于现有的挖掘算法存在众多缺陷，挖掘出的过程模型可能会与真实日志之间存在偏差。一致性检验用于检测模型与日志之间是否存在偏差，主要度量标准有拟合度、精确度、泛化度、简洁度。泛化度用于度量模型泛化日志行为的程度，即未来日志行为符合模型的程度，是过程挖掘中防止模型过拟合的一种度量标准。计算泛化度的主要困难是需要度量未知的日志行为，因此现有的计算泛化度的算法相对于其他度量标准来说并不多。

过程树算法[6]根据过程模型构建过程树，将事件日志在过程树上重演，根据树中结点被访问频率计算泛化度。该算法的主要缺点是需要先根据过程模型构建过程树，时间复杂度比较高。基于校准的算法[7-8]将每个事件作为一个独立的事件，计算事件属于每个状态的概率，根据状态的被访问次数及状态发生的活动数计算泛化度。该算法依赖于贝叶斯假设[9]，要求每个状态可能发生的活动数量是未知的，并且服从多项式分布，而通常情况下每个状态只有有限个可以发生的活动。该算法没有给出状态的精确定义，并且事件日志规模较大时对每一个事件进行计算会非常耗时。反校准算法[10]通过计算最大反校准距离与最大反校准的恢复距离之间的欧几里得距离来计算泛化度,为了降低时间复杂度该算法对最大反校准的长度进行限制，导致测量结果不准确，并且相对于其他算法该算法的时间复杂度仍然很高。

本研究针对基于校准[11]的泛化度算法[7-8]依赖于概率分布和时间复杂度高的缺点，提出一种类似于精确度自动机[7]的泛化度自动机算法,将Petri网模型中的标识作为状态，并且借鉴过程树算法[6]中的泛化度计算方法而不依赖于贝叶斯假设。

1 基本概念

过程模型的表示方法有多种，如Petri网[12-13]、变迁系统、工作流网、BPMN、YAWL等。Petri网图形表示直观简单并且可以与其他表示方法互相转换，因此本研究采用Petri网表示方法。下面介绍本研究所用到的基本概念：

定义1(Petri网)[14]设A为活动的集合，关于A的Petri网是一个元组N=(P,T,F,α,M,m0,mf)，其中P是库所集合,T是变迁集合,且P∩T=∅，F=(P×T)∪(T×P)是有向弧集合,M是标识集合,m0是初始标识，mf为结束标识，α:T→A是一个将变迁映射到活动的函数。

标识M表示库所含有token的情况，例如M(p)=k表示库所p含有token的数量为k。设变迁t∈T，则·t是t的前集，即含有有向弧指向t的库所集合。t·是t的后集，即从t发出的有向弧所指向的库所的集合。当·t中每一个库所至少有一个token时，t可以引发。t引发后·t中每一个库所减少一个token，t·中每一个库所增加一个token。

如果存在一个变迁引发序列σ=t1t2…tn使标识从M转变到M′，即M[σ>M′，则称标识M′是从M可达的。如果m0[σ>mf,则σ为完整变迁引发序列。

定义2(事件日志)[1]事件日志L是迹的多重集，迹σ∈L是一个有限活动序列，σ=<σ1,σ2,…σ|σ|>，σi表示迹σ在第i位置的活动。

定义3(校准)[7]设A为活动的集合，σ∈A*是关于活动A的迹，关于活动A的Petri网N=(P,T,F,α,M,m0,mf)，迹σ与模型N的校准移动序列γ∈(A≫×T≫)*(≫表示没有与之对应的活动)。π1(γ)是序列在活动集合A上的投影，π2(γ)是序列在变迁集T上的投影。

对任意 (a,t)∈γ，校准可分为三种情况：当a∈A且t=≫时，日志移动；当a=≫且t∈T时，模型移动；当a∈A且t∈T时，同步移动。

代价函数是校准中偏差(日志移动、模型移动)的代价总和，最优校准是代价函数值最小的校准，最优校准可能不止一个。

2 过程模型泛化度

2.1 个人贷款流程

个人贷款流程是电子商务领域的典型应用，具有很强的流程性，是过程挖掘领域的典型实例。图1中的Petri网模型描述的是简化的个人贷款流程,该模型是从2012年BPI挑战[15]提供的日志中选取的部分事件日志通过挖掘算法和手工创建得到的。贷款用户首先需要登记贷款信息(register)，然后分成两个并行执行的过程，分析人员为用户提供与其申请相匹配的贷款产品(offers)，审核人员审查用户申请(validate)。如果用户是新用户，可能需要另外一个分析人员对用户的需求进行分析并提供更加合理的产品(extra offering)。同时风险分析人员对申请进行风险分析(risk analysis)。贷款经理根据风险分析及审核的结果做出是否同意贷款的决定(decide)。如果用户对申请结果不满意可以提出申诉(objection)，并重新申请(re-register),否则贷款过程结束并记录(archive)。

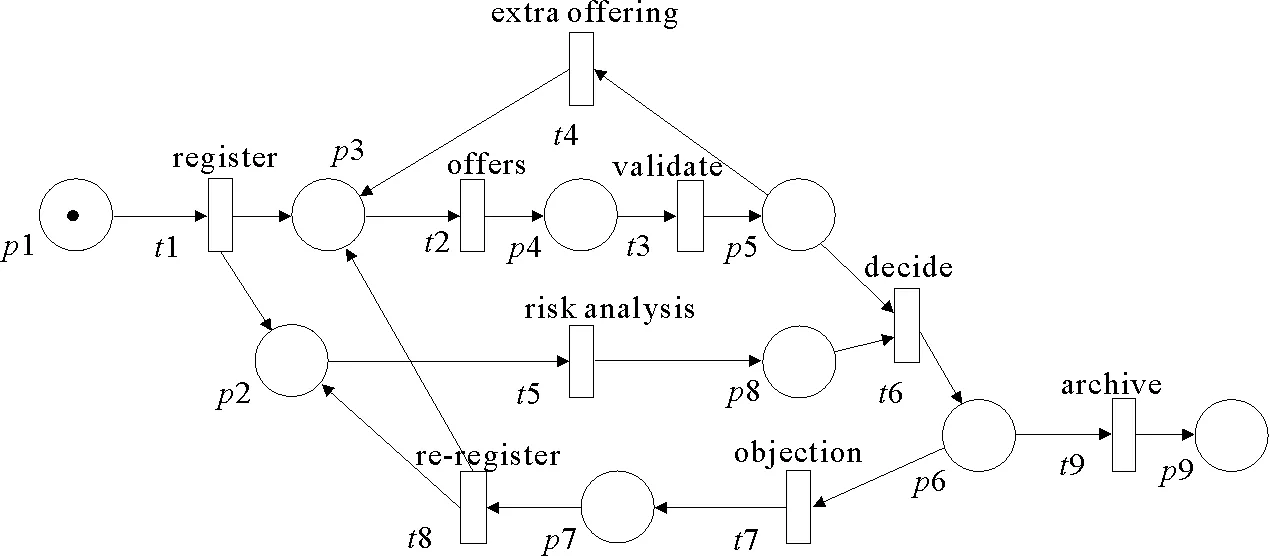
图1 个人贷款流程Petri网模型

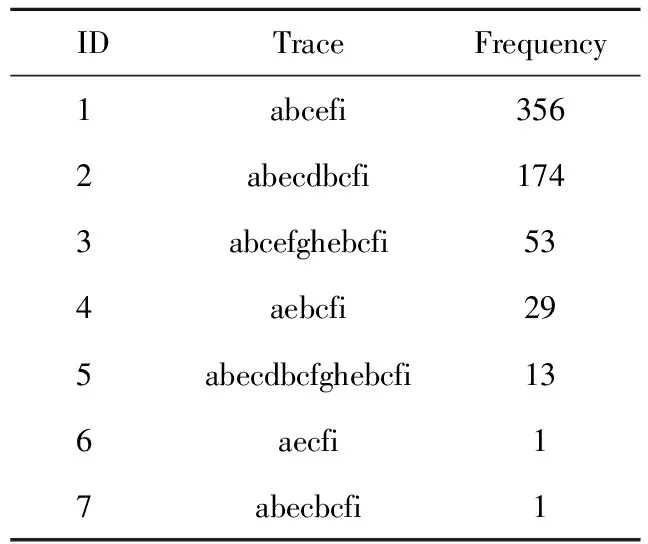
IDTraceFrequency1abcefi3562abecdbcfi1743abcefghebcfi534aebcfi295abecdbcfghebcfi136aecfi17abecbcfi1

表1是从图1 Petri网模型对应的事件日志中截取的7条迹组成的事件日志，其中第一列是日志中迹的编号，第二列是迹，第三列是迹出现的频率。为了简单起见，变迁t1,t2,t3,t4,t5,t6,t7,t8,t9对应的活动分别用字母a,b,c,d,e,f,g,h,i表示。

2.2 泛化度自动机

通常一个过程模型不应该只允许日志中的行为，否则这个模型是过拟合的[1](overfitting)。泛化度用于度量模型泛化日志行为的程度。计算泛化度的主要困难是需要考虑未知的行为，而日志中的行为是模型行为的真实反映，可以根据日志中已有的行为预测未知行为能否执行。

对拟合度很低的日志和模型进行泛化度计算是毫无意义的，为了不受拟合度的影响，用完全拟合的事件日志计算泛化度。将事件日志与Petri网模型校准得到校准序列，再将校准序列投影到变迁集可以得到完全拟合的事件日志。

过程树算法[6]根据过程树结点的被访问次数计算泛化度，一个树结点被访问的次数越多，则越能确定这个结点是正确的。如果过程树中有些结点很少被访问到，则泛化度会比较低。借鉴这个思想，将完全拟合的事件日志在Petri网模型上重演，根据标识状态变化情况构建泛化度自动机，并记录状态的被访问次数及状态发生的活动集合。状态的被访问次数与状态发生的活动数之比越高则状态越可靠，下次再访问该状态而不引发新活动的可能性越大，则泛化度越高。假设状态S被访问n次，发生的活动数是w,如果n很大w很小，则下次再访问S时引发新活动的可能性很小。如果n和w差不多大，则下次再访问S时很可能会引发新活动。下面给出泛化度自动机和泛化度的定义：

定义4(泛化度自动机) 泛化度自动机是一个元组GA=(S,SE,AT,NT,T,s0),其中S⊆M是标识状态集合，M是Petri网的可达标识集合，SE⊆S×T×S是状态间的带标签的有向边集合，AT是状态被访问次数集合，NT是每个状态发生的活动集合的集合，T是Petri网的变迁集合，s0=m0是初始状态。

定义5(泛化度) 设N=(P,T,F,α,M,m0,mf)是关于活动集合A的Petri网，L是关于活动集合A的事件日志，α(L)是完全拟合的事件日志，GA=(S,SE,AT,NT,T,s0)是将α(L)在N上重演得到的泛化度自动机，则泛化度为：

(1)

对泛化度自动机中的每一个状态Si∈S，ATi表示状态Si的被访问次数，NTi表示迹在Petri网模型重演时统计的在状态Si所发生的活动集合。为了防止出现分母为0的情况，当NTi∉NT时令|NTi|=1。这是合理的，因为Si∈S和NTi∉NT两个条件同时满足的状态只有泛化度自动机中的最后一个状态(mf)，而每一个完全拟合的迹都会经过最后一个状态，即当日志中的迹足够多时公式中第二个求和项会接近于0。

算法1构建泛化度自动机

输入：事件日志L，Petri网模型N

输出：泛化度自动机

步骤：

1．S←{s0},SE←∅,AT←∅,NT←∅;

2．α(L)←alignment(L,N) ;

3．for allσ∈α(L) do

4． for alle∈σdo

5． if(si[e>sj) then

6． if(sj∉S) then

7．S←(S∪ {sj});

8．ATj←1;

9．AT←(AT∪{ATj});

10． elseATj←(ATj+1) ;

11． end if；

12． end if；

13． if(NTi∉NT) then

14．NTi←{e};

15．NT←(NT∪{NTi});

16． elseNTi←(NTi∪{e});

17． end if；

18． if((si,e,sj)∉SE) then

19．SE←(SE∪{(si,e,sj)});

20． end if；

21． end；

22．end；

23．GA←(S,SE,AT,NT,T,s0) ;

24．returnGA;

如果日志中有m条轨迹，平均每条轨迹有n个事件，则泛化度自动机算法时间复杂度为O(mn)，如果Petri网中共有s个状态则基于校准算法的时间复杂度为O(smn)。过程树算法需要根据过程模型构建过程树，遍历过程树，时间复杂度也高于泛化度自动机算法。

表2 迹的校准序列

下面对图1 Petri网模型N和表1事件日志计算泛化度。首先将事件日志与Petri模型校准，再将校准序列投影到变迁集得到完全拟合的事件日志α(L)。表2是迹的一个最优校准，其中第5列是模型移动，是拟合后的迹。将α(L)在N上重演根据标识状态变化情况得到泛化度自动机。

图2是根据图1 Petri网和表1事件日志得到的泛化度自动机，图中S0-S9是状态，状态右上角的两个数字分别是状态被访问次数和状态发生的活动数。例如状态S1被访问693次，发生的活动数是2 (t2和t5)。根据泛化度计算公式 (1)，泛化度为：Generation(N,L)=0.941 2,用过程树算法[6]得到的泛化度为0.948 7，基于校准的算法[7]得到的泛化度为0.950 3。

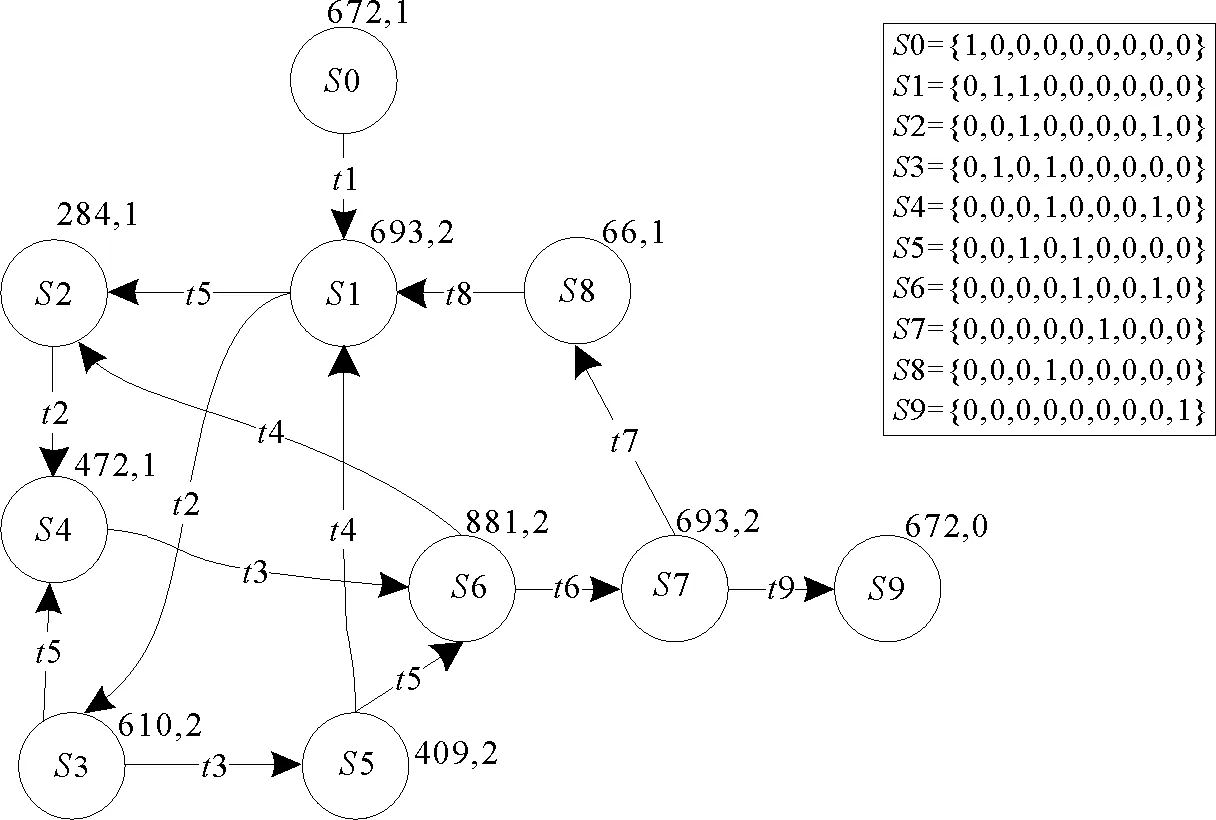
图2 泛化度自动机

3 仿真实验

下面通过仿真实验来评价本文所提出的泛化度自动机算法，实验在开源软件ProM6[16]上进行。试验将泛化度自动机算法与其他经典算法作对比，以验证其正确性与实用性。

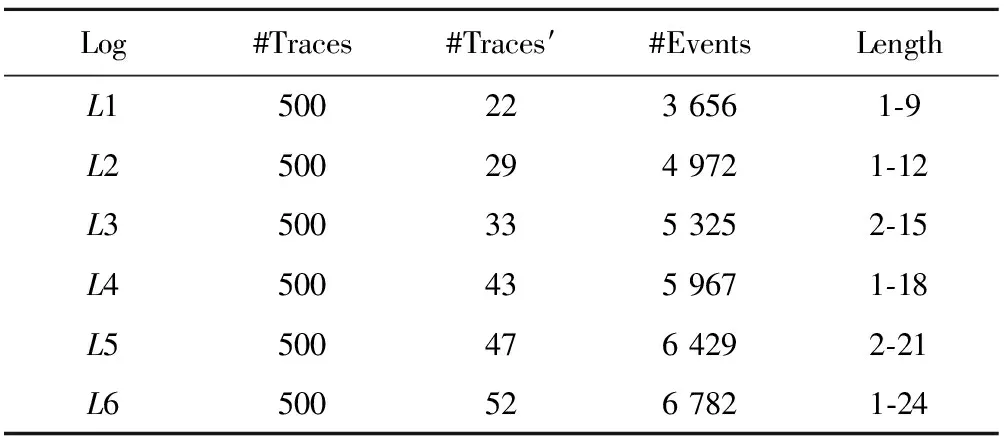
表3 事件日志信息

表3是从图1所示的个人贷款模型N所对应的事件日志中截取的6段事件日志的基本信息。每个事件日志含有500条迹(#Traces)，但是日志中的不同迹数(#Traces′)、事件数(#Events)、迹的长度(Length)不同，并且递增。随着事件日志更全面地覆盖模型的标识状态，状态的可信度增加，泛化度也会增加。通过本实验可以验证算法是否具有正确性和实用性。

图3是对不同事件日志测量泛化度的结果。4种算法的泛化度值都呈递增趋势，过程树算法(gt)[6]、基于校准的算法(ga)[7]、泛化度自动机算法(gs)得到的泛化度值相近，而反校准算法(gc)[10]因为对最大反校准的长度进行了限制，得到的值偏低。

图4是计算泛化度所用的时间。过程树算法(gt)需要校准和构建过程树所用时间多于基于校准的算法(ga)和泛化度自动机算法(gs)。虽然本研究所提出的算法也需要校准，但是没有对日志中的每个事件单独处理，因此所用时间少于基于校准的算法(ga)。反校准算法(gc)为了得到最大反校准需要遍历整个模型，用时最多。

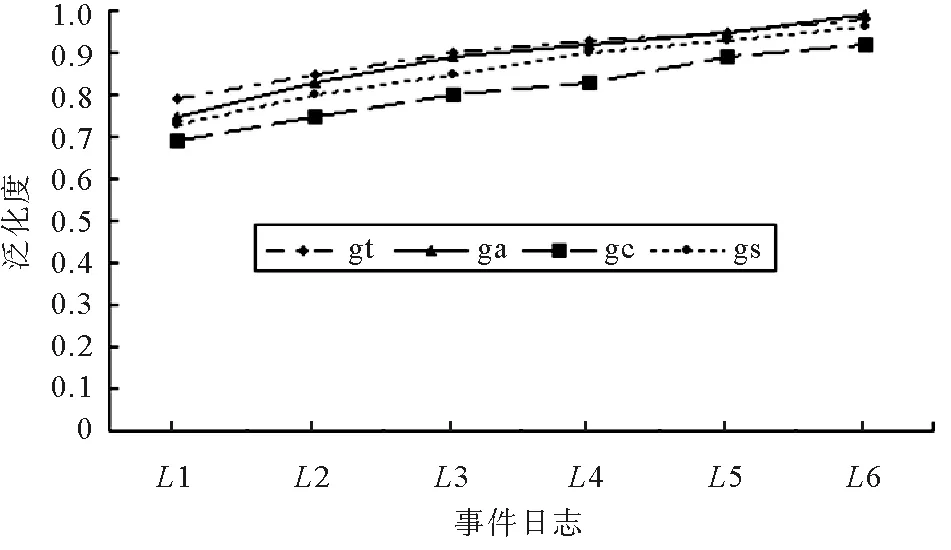
图3 同一模型不同事件日志泛化度

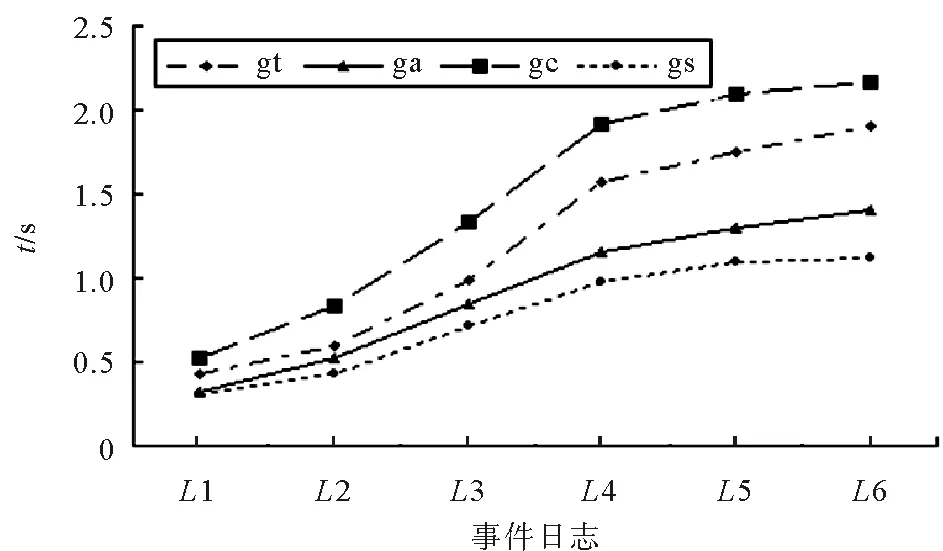
图4 计算时间

通过仿真实验可以得出本研究所提出的泛化度算法可以得到与基于校准的算法和过程树算法相似的结果，而用时少于这两种算法。

4 结论

针对基于校准的泛化度算法的缺点，提出一种泛化度自动机算法。将事件日志与过程模型校准得到完全拟合的事件日志，将完全拟合的事件日志在Petri网模型上重演，根据标识状态变化情况构建泛化度自动机。根据泛化度自动机中状态被访问次数及状态发生的活动数计算泛化度。通过实例介绍了泛化度的计算方法及过程。该算法相对于其他经典算法最大的特点是表示直观简单，不依赖于概率分布并且时间复杂度低。仿真实验验证了算法的正确性及实用性。通过本文所提出的算法可以得到模型的泛化度，如何利用所得到的泛化度去改进模型，避免模型过拟合是本研究以后的工作目标。

[1]AALST W V D.Process mining:Discovery,conformance and enhancement of business processes[M].Berlin:Springer,Publishing Company,2011:191-213.

[2]AALST W V D,ADRIANSYAH A,MEDEIROS A K A D,et al.Process mining manifesto[C]// International Conference on Business Process Management.Springer,Berlin,Heidelberg,2011:169-194.

[3]李洪霞,杜玉越.业务过程管理研究现状与关键技术[J].山东科技大学学报(自然科学版),2015,34(1):22-28.

LI Hongxia,DU Yuyue.A survey of research issues and key technology for business process management[J].Journal of Shandong University of Science and Technology(Natural Science),2015,34(1):22-28.

[4]鲁法明,曾庆田,段华,等.一种并行化的启发式流程挖掘算法[J].软件学报,2015,26(3):533-549.

LU Faming,ZENG Qingtian,DUAN Hua,et al.Parallelized heuristic process mining algorithm[J].Journal of Software,2015,26(3):533-549.

[5]祁宏达,杜玉越,刘伟.一种基于可达标识的过程模型修复方法[J].山东科技大学学报(自然科学版),2017,36(1):118-124.

QI Hongda,DU Yuyue,LIU Wei.Process model repairing method based on reachable markings[J].Journal of Shandong University of Science and Technology(Natural Science),2017,36(1):118-124.

[6]BUIJS J C A M,DONGEN B F V,AALST W M P V D.On the role of fitness,precision,generalization and simplicity in process discovery[J].Springer Berlin Heidelberg,2012,7565(3) :305-322.

[7]ADRIANSYAH A.Aligning observed and modeled behavior[D].Eindhoven:Eindhoven University of Technology，2014:129-166.

[8]AALST W M P V D,ADRIANSYAH A,DONGEN B V.Replaying history on process models for conformance checking and performance analysis[J].Wiley Interdisciplinary Reviews:Data Mining and Knowledge Discovery.2012,2(2):182-192.

[9]BOENDER C G E.A bayesian analysis of the number of cells of a multinomial distribution[J].The Statistician,1983,32(1/2):240-248.

[10]DONGEN B F V,CARMONA J,CHATAIN T.A unified approach for measuring precision and generalization based on anti-alignments[M].Berlin:Springer International Publishing，2016.

[11]王路,杜玉越.一种基于校准的模型问题域识别方法[J].山东科技大学学报(自然科学版),2015,34(1):42-46.

WANG Lu,DU Yuyue.An alignment-based identifying method of the problem areas within process models[J].Journal of Shandong University of Science and Technology(Natural Science),2015,34(1):42-46.

[12]DU Y Y,QI L,ZHOU M C.Analysis and application of logical Petri nets to E-commerce systems[J].IEEE Transactions on Systems Man & Cybernetics Systems,2014,44(4):468-481.

[13]DU Y Y,NING Y.Property analysis of logic Petri nets by marking reachability graphs[J].Frontiers of Computer Science,2014,8(4):684-692.

[14]吴哲辉.Petri网导论[M].北京：机械工业出版社，2006.

[15]DONGEN B F V.BPI challenge 2012.Dataset[DB].http://dx.doi.org/10.4121/uuid:3926db30-f712-4394-aebc-75976070e91f.

[16]MEDEIROS A K A D,WEIJTERS A J M M,Aalst W M PVD.Genetic process mining:An experimental evaluation[J].Data Mining and Knowledge Discovery.2007,14(2):245-304.