基于分数布朗运动的Knight不确定环境下的期权定价

，

(1.山东科技大学 信息工程系，山东 泰安 271000； 2.山东科技大学 数学与系统科学学院，山东 青岛 266590)

金融衍生资产定价是现代金融理论的核心内容，Black和Scholes假定股票价格服从几何布朗运动，得出了著名的Black-Scholes公式[1]。而金融实证表明，股票市场价格具有长期依赖性和自相似性[2]，用分数布朗运动来代替几何布朗运动更贴近市场规律。股票价格由分数布朗运动驱动的期权定价模型吸引了许多研究者的注意[3-6]。

1921年，美国经济学家Knight[7]首次提出在金融市场上经常会有无法用单一概率测度度量的风险，称为Knight不确定性风险。在文献[8]中，Chen和Larry利用BSDE[9]的有关理论第一次建立起数学模型，体现了Knight不确定性。张慧等[10]在Knight不确定环境下，假设股票价格过程服从几何布朗运动，建立了欧式期权的最小定价模型，并求出了模型的显示解。韩立岩等[11]利用模糊测度的思想，建立了Knight不确定环境下基于模糊测度的期权定价模型。费文银等[12]对Knight不确定环境下带通胀的最优投资和消费模型研究，得到了对应问题的最优投资组合模型。王向荣等[13]假设股票价格服从几何布朗运动的条件下，讨论了Knight不确定环境下，多资产彩虹期权的动态定价，给出了彩虹期权的上下界区间。黄虹等[14]讨论了股票价格服从Levy假设下的期权定价问题。

本文在股票价格服从分数布朗运动的假设下，讨论Knight不确定环境下的期权定价问题。利用Knight不确定环境下概率测度不唯一的特性，对不确定参数引入一个可行控制集合Θ来刻画金融市场上的Knight不确定性,建立了期权的动态定价模型以及欧式期权在一个概率测度集合上的最小定价模型。

1 资产价格模型与测度变换

设(Ω，F，Ft，P)是一个具有σ域流的概率空间，其中{Ft}0≤t≤T是由分数布朗运动{BH(t),t∈R}产生的自然σ域流。假设分数市场上有两种资产，一种为无风险资产(债券)，另一种为风险资产(股票)。其价格过程分别满足以下方程：

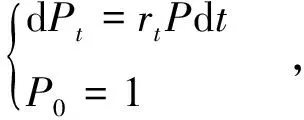
(1.1)

(1.2)

其中，rt≥0,μt是Ft-可测的适应过程，σ为常数，rt、μt和σ分别表示t时刻无风险利率、风险资产在t时刻的预期收益率和波动率。

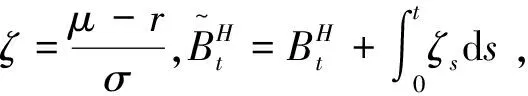
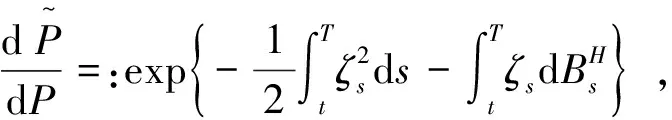
(1.3)

引理1[6]任意有界FT可测的期权V∈L2(P,FT,R)在任意时刻t∈[0,T]的价格V(t)由(1.4)给出：

(1.4)

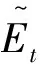
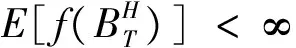
(1.5)

2 Knight不确定环境下的欧式期权定价

为了刻画金融市场上的Knight不确定性，引入一个可行控制集合Θ：

Θ={(θt)0≤t≤T,|θt|≤k,a.e.t∈[o,T]}。

(2.1)

其中k>0为常数。文献[4]把θt称为κ-ignorance。

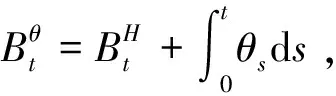
(2.2)

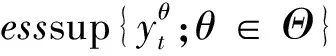
定理2.1在无套利自融资假设下，设欧式期权到期收益为f(ST)，则在Knight不确定环境下，欧式期权在t时刻的动态价格为：

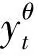
(2.3)

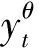
(2.4)

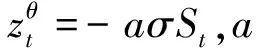
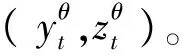
由引理1得：

由引理2知：

证毕。

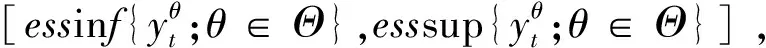
证明：由引理1知：

则∀θ1,θ2∈Θ，|θ1|≤k,|θ2|≤k，由拟条件期望的单调性，当θ1≥θ2，有：yθ1(t)≥yθ2(t)。

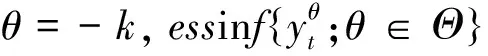
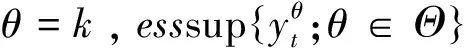
证毕。

3 Knight环境下金融市场中的欧式期权最小定价

由于Knight环境的影响，虽然投资者不确定该用Φ中的哪个概率测度来对期权进行定价，但从保守角度考虑，投资者一般会给出期权的最小定价，本节研究Knight环境下分数金融市场中的欧式期权最小定价。

假设债券价格方程与风险中性假设下的股票价格方程为：

到期日，Knight环境下执行价格为K的欧式看涨期权和欧式看跌期权的最小定价分别为：

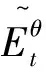
定理3.1假设rt=r,σt=σ为常数，则

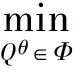
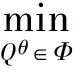
其中

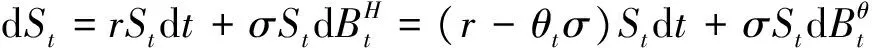
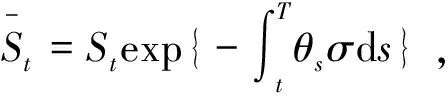
由引理1得到概率测度Qθ下：

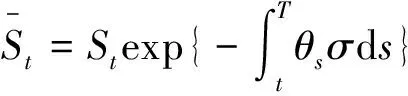
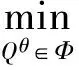
同样得到：

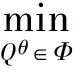
证毕。

定理3.2假设rt,θt为非随机函数，σ为常数，则

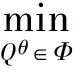
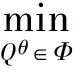
其中

证明：由引理1得

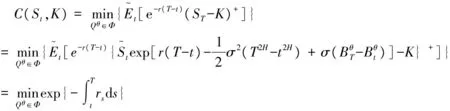
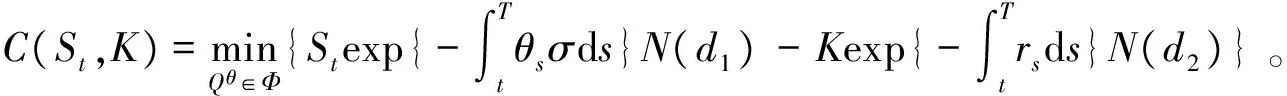
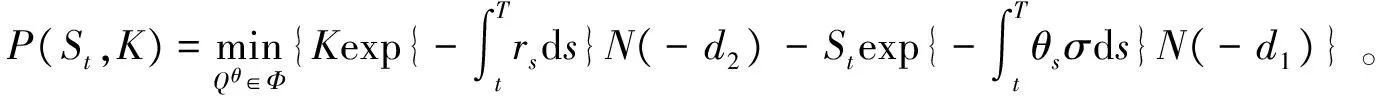
证毕。

4 结论

本文在标的资产由分数布朗运动驱动的假设条件下，研究了Knight不确定环境下期权定价问题。建立了期权在一族概率测度下的动态价格模型，并得到了任意时刻期权的动态价值区间。最后得到了Knight不确定环境下的欧式期权定价公式。

[1]BLACK F,SCHOLES M.The pricing of options and corporate liabilities[J].Journal of Political Economy，1973,81(3):637-654.

[2]FAMA E.The behavior of stock market price[J].The Journal of Business,1965,38(1):34-105.

[3]李蕊.分数布朗运动下带红利的欧式期权定价[J].兰州理工大学学报,2012，38(4):162-164.

LI Rui.European option pricing with dividend and fractional Brownian motion[J].Journal of Lanzhou University Technology,2012，38(4):162-164.

[4]刘韶跃,杨向群.分数布朗运动环境中混合期权定价[J].工程数学学报,2006,23(1):153-157.

LIU Shaoyue,YANG Xiangqun.Pricing of compound option in a fractional Brownian motion environment[J].Chinese Journal of Engineerring Mathematicas,2006,23(1):153-157.

[5]李施荔.分数布朗运动下的期权定价问题研究[D].哈尔滨:哈尔滨工程大学,2012.

[6]HU Y.Fractional white noise calculus and applications to finance[J].Infinite Dimensional Analysis,Quantum Probability and Related Topics,2003,6(1):1-32.

[7]KNIGHT F H.Risk Uncertainty and Profit[M].Boston:Houghton Mifflin,1921.

[8]CHEN Z J,EPSTEIN L.Ambiguity,risk,and asset return in continuous- time[J].Econometrica,2002,70:1403-1433.

[9]PARDOUX E,PENG S.Adapted solution of a backward stochastic differential equation[J].Systems and Control Letters,1990,14(1):55-61.

[10]张慧,聂秀山.Knight不确定环境下欧式期权的最小定价模型[J].山东大学学报(理学版),2007,42(11):121-126.

ZHANG Hui,NIE Xiushan.Minimal pricing models of European stock options under knight uncertainty[J].Journal of Shandong University(Natural Science),2007,42(11):121-126.

[11]韩立岩,周娟.Knight不确定环境下基于模糊测度的期权定价模型[J].系统工程理论与实践,2007,27(12):123- 131.

HAN Liyan,ZHOU Juan.Option pricing with fuzzy measures under knightian uncertainty[J].System Engineering Theory and Practice,2007,27(12):123-131.

[12]费文银,李淑娟.Knight不确定环境下带通胀的最优投资和消费模型研究[J].工程数学学报，2012,29(6):799-806.

FEI Wenyin,LI Shujuan.Study on optimal consumption and portfolio with inflation under knightian uncertainty[J].Chinese Journal of Engineering Mathematicas,2012,29(6):799-806.

[13]王向荣,孟令巧,张婉婷.不确定环境下彩虹期权价格上下界的估计[J].科技创新导报,2013(7):222-226.

WANG Xiangrong,MENG Lingqiao.ZHANG Wanting.Upper and lower bounds on rainbow option prices under uncertainty[J].Science and Technology Innovation Herald,2013(7):222-226.

[14]黄虹,王向荣.Knight不确定环境下Lēvy市场中的期权定价[J].数学的实践与认识,2016，46(20):87-92.

HUANG Hong,WANG Xiangrong.Option pricing under knight uncertainty in Lēvy market[J].Mathematicas in Practice and Theory,2016，46(20):87-92.

[15]陈松男.金融工程学[M].上海：复旦大学出版社,2002.