G′/G展开法在(3+1)维KP方程中的应用

，

(聊城大学 数学科学学院，山东 聊城 252059)

在数学物理、工程力学等许多领域中，存在着大量的模型可以用偏微分方程来描述。例如，热流动、波的传播、大部分人口统计模型以及化学反应性材料的色散现象等。另外，流体动力学、量子力学、电力学、离子体物理浅水波的传播等都需要偏微分方程来刻画。因此，非线性发展方程得到人们的广泛关注[1]，许多学者也在非线性方程求解这一领域取得了巨大的成就[1]。在非线性波及孤立子理论的物理问题中，KP方程占有重要的位置[2,3]，本文研究(3+1)维KP方程

(ut+6unux+ruxxx)x+αuyy+βuzz=0

其中，u=u(t,x,y,z)为未知函数,r、α、β为任意常数,n为待定常数。

关于求解非线性偏微分方程精确解已经有很多方法，如齐次平衡法[4,5,6,11]、双曲函数法[7]、Hirota方法[10]和Jacobi椭圆函数展开法[4,8]等。本文将运用G′/G展开法[11-19]和齐次平衡原理[4-6]求解KP方程精确行波解。

1 (3+1)维KP方程

对于方程

(ut+6unux+ruxxx)x+αuyy+βuzz=0，

(1.1)

首先作行波变换

u(x,t)=u(ξ),ξ=x+y+z-Ct,

(1.2)

其中C为波速。

将式(1.2)代入(1.1)，化简可得到关于u=u(ξ)的方程

-Cu″+6nun+1u′2+6uu″+ru(4)+αu″+βu″=0。

(1.3)

对(1.3)求一次积分，得

-Cu′+6unu′+rum+αu′+βu′=A,

(1.4)

其中，A为积分常数。

假设方程(1.4)的解能够表示成如下形式:

(1.5)

这里G=G(ξ)，并且满足二阶线性常微分方程

G″+λG′+μG=0。

(1.6)

由(1.4)式和(1.5)式求得

(1.7)

(1.8)

(1.9)

(1.10)

把式(1.5)～(1.9)代入式(1.4)后，平衡最高阶导数项um和非线性项unu′的指数，即mn+m+1=m+3，mn=2。

1) 当n=1时，

(ut+6uux+ruxxx)x+αuyy+βuzz=0,

(1.11)

平衡最高阶导数项um和非线性项uu′的指数，即m=2,故方程(1.1)可能存在G′/G解。

2) 当n=2时，

(ut+6u2ux+ruxxx)x+αuyy+βuzz=0,

(1.12)

平衡最高阶导数项um和非线性项u2u′的指数，即m=1，故方程(1.1)可能存在G′/G解。

综上所述，当n=1，2时方程(1.1)可能有G′/G解。

2 KP方程的G′/G解

1) 当n=1，m=2时，形式解为

(2.1)

同样求得

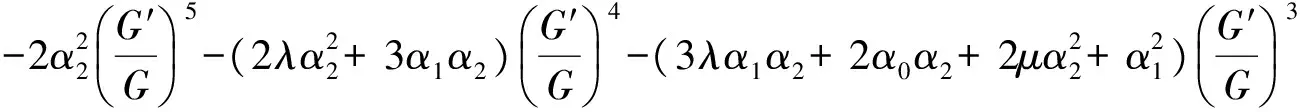
(2.2)

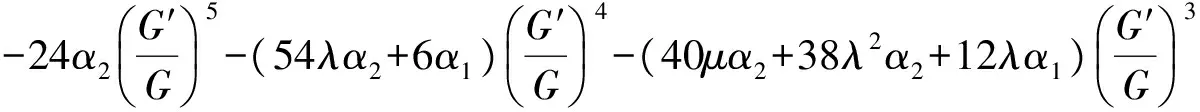
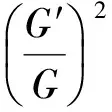
-6λμ2α2-2μ2α1-α1μλ2,

(2.3)

把式(2.1)～(2.3)代入式(1.4)中，求得

-(8λ3α2-2Cλα2+ 52μλα2+ 18μα1α2+ 2αλα2+ 2βλα2+ 7λ2α1

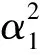
-6α2μ2λ-α1μλ2+Cμα1-2α1μ2-αμα1-βμα1-6μα1α0+A。

(2.4)

(2.5)

(2.6)

(2.7)

(2.8)

(2.9)

(2.10)

求解方程组(2.5)～(2.10)，可得

A=0，

(2.11)

α1=-2λ，

(2.12)

α2=-2，

(2.13)

C=λ2+8μ+α+β+6α0。

(2.14)

将式(2.11)～(2.14)代入式(2.1)，求得

(2.15)

其中，C=x+y+z-(λ2+8μ+α+β+6α0)t。

(2.16)

把(1.5)式代入(2.15)式,可以得到以下三种形式的解:

当λ2-4μ>0时，

其中，ξ=x+y+z-(λ2+8μ+α+β+6α0)t，C1，C2均为任意常数。

当λ2-4μ<0时，

其中，ξ=x+y+z-(λ2+8μ+α+β+6α0)t，α0，C1，C2均为任意常数。

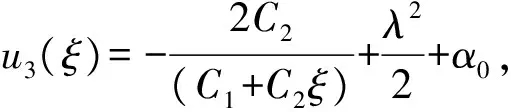
其中，ξ=x+y+z-(λ2+8μ+α+β+6α0)t，α0、C1、C2均为任意常数。

2) 当n=2，m=1时，根据讨论，得到

(2.17)

同样地求得：

(2.18)

(2.19)

(2.20)

⋮

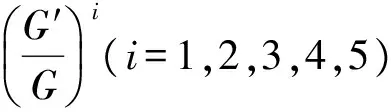
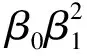
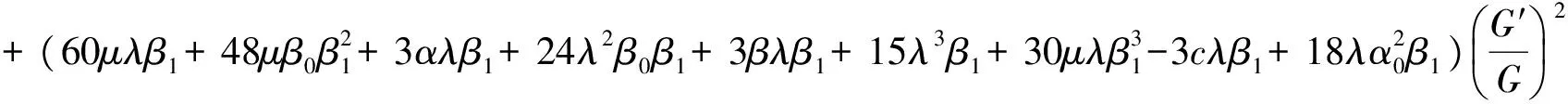
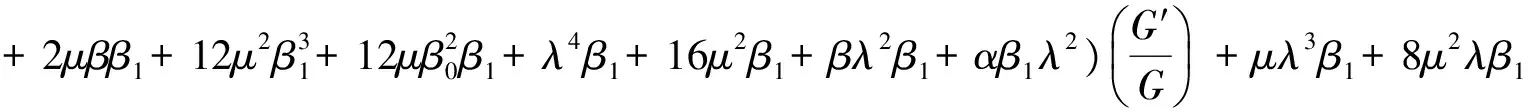
(2.21)

(2.22)

(2.23)

(2.24)

(2.25)

(2.26)

(2.27)

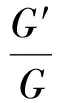
3 结论

本文探讨了G′/G展开法在求KP方程精确解中的应用。由上述讨论，得到了新的周期函数解、指数函数解以及包含更多参数的精确解。推广的KP方程有多种形式的精确解,应用范围广泛，应用本文的方法，不仅能够求出推广的KP方程的G′/G解,也可以求出其他非线性方程的精确解。

[1]刘睿.相容性方法在求解变系数发展方程中的应用[J].河北师范大学学报(自然科学版),2011,35(5):442-447.

LIU Rui.Applications of the compatible method to solving variable coefficient evolution equation[J].Journal of Heibei Normal University (Natural Science),2011,35(5):442-447.

[2]范恩贵,张鸿庆.非线性波动方程的孤波解[J].物理学报,1997,46(7):1254-1258.

FAN Engui,ZHANG Hongqing.The solitary wave solutions for a class of nonlinear wave equations[J].Journal of Physics,1997,46(7):1254-1258.

[3]郝瑞宇.可变参量光纤系统中光脉冲的传播的特征研究[D].太原：山西大学,2007：44-71.

[4]王明亮,李志斌,周宇斌.齐次平衡原则及其应用[J].兰州大学学报(自然科学版),1999,35(3):8-16．

WANG Mingliang,LI Zhibin,ZHOU Yubin.Homogeneous balance principle and its application[J].Journal of Lanzhou University (Natural Science),1999,35(3):8-16.

[5]刘式适,傅遵涛,刘式达,等.Jacobi 椭圆函数展开法及其在求解非线性波动方程中的应用[J].物理学报,2001,50(11):2068-2073.

LIU Shikuo,FU Zuntao,LIU Shida,et al.Expansion method about the Jacobi elliptic function and its applications to nonlinear ware equations[J].Journal of Physics,2001,50(11):2068-2073.

[6]张辉群.齐次平衡方法的扩展及应用[J].数学物理学报,2001,21(3):321-325.

ZHANG Huiqun.Extension and applications of the homogeneous balance method[J].Journal of Mathematical Physics,2001,21(3):321-325.

[7]扎其劳.修正双曲函数与非线性发展方程的精确解[J].内蒙古师范大学学报(自然科学版),2007,36(1):15-21.

ZHA Qilao.Modified hyperbolic function method and exact solutions to nonlinear evolution equations[J].Journal of Inner Mongolia Normal University (Natural Science),2007,36(1):15-21.

[8]赵云梅,芮伟国.Equal Width波方程的各种椭圆函数周期解和孤子解[J].四川师范大学学报(自然科学版),2008,31(2):190-193．

ZHAO Yunmei,RUI Weiguo.All kinds of the periodic solutions of Jacobian elliptic function type and the solutions for Equal Width wave equation[J].Journal of Sichuan Normal University (Natural Science),2008,31(2):190-193.

[9]韩家骅,陈良,徐勇,等.组合及二维KdV方程的显式精确解[J].安徽大学学报(自然科学版)2004,28(1):35-41.

HAN Jiahua,CHEN Liang,XU Yong,et al.Explicit exact solutions to the combined KdV equation and two-dimensional KdV equation[J].Journal of Anhui University (Natural Science),2004,28(1):35-41.

[10]林麦麦,段文山,吕克璞.Hirota方法求解KP方程的多孤子解[J].西北师范大学学报(自然科学版),2004,40(3):26-34.

LIN Maimai,DUAN Wenshan,LÜ Kepu.The muliti-soliton solution of KP equation by Hirota method[J].Journal of Northwest Normal University (Natural Science),2004,40(3):26-34.

[11]张国栋,秦清锋.齐次平衡法在微分方程中的应用[J].中国新技术新产品,2010(21):243-244.

ZHANG Guodong,QIN Qingfeng.Application of homogeneous balance method in differential equation[J].Journal of New Technology and New Products in China,2010(21):243-244.

[12]施业琼.应用(G′/G)-展开法求解高阶非线性薛定谔方程[J].广西工学院学报,2009,20(3):45-49.

SHI Yeqiong.Solving the higher-order nonlinear Schrodinger equation by the (G′)/(G)-expansion method[J].Journal of Guangxi Institute of Technology,2009,20(3):45-49.

[13]牛艳霞,李二强,张金良.利用(G′/G)-展开法求解2+1维破裂孤子方程组[J].河南科技大学学报(自然科学版),2008,29(5):73-76.

NIU Yanxia,LI Erqiang,ZHANG Jinliang.(G′/G)-expansion method to solve the 2+1 dimensional breaking solition equations[J].Journal of Henan University of Science and Technology (Natural Science),2008,29(5):73-76.

[14]李帮庆,马玉兰.(G′/G)展开法和(2+1)维非对称Nizhnik-Novikov-Veselov系统的新精确解[J].物理学报,2009，58(7):4373-4378.

LI Bangqing,MA Yulan.(G′/G)-expansion method and new exact solutions for (2+1)-dimensional asymmetrical Nizhnik-Novikov-Veselov system[J].Journal of physics,2009，58(7):4373-4378.

[15]WANG M L, LI X Z,ZHANG J L.The (G′/G)-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics[J].Physics Letters A,2008,372(4):417-423.

[16]郭冠平,周国中,何宝钢.G′/G展开法对非线性耦合Klein-Gordon方程组的精确解磁[J].浙江师范大学学报(自然科学版),2010,33(3):286-290.

GUO Guanping,ZHOU Guozhong,HE Baogang.G′/Gexpansion method for nonlinear exact solutions of magnetic coupling Klein-Gordon equation set[J].Journal of Zhejiang Normal University (Natural Science),2010,33(3):286-290.

[17]魏帅帅,李凯辉,刘汉泽.G′/G展开法在Riccati方程中的应用[J].河南科技大学版(自然科学版),2015,36(5):92-96.

WEI Shuaishuai,LI Kaihui,LIU Hanze.G′/Gexpansion method in the application of Riccati equation [J].Journal of Henan University of Science and Technology (Natural Science),2015,36(5):92-96.

[18]LIU Hanze,XIN Xiangpeng.Symmetries,integrability and exact solutions to the (2+1)-dimensional Benney types of equations[J].Communications in Theoretic at Physics,2016,66(8):155-162.

[19]张丽香,刘汉泽,辛祥鹏.广义(3+1)维Zakharov-Kuznetsov方程的对称、约化、精确解和守恒率[J].物理学报,2017,66(8):1-7.

ZHANG Lixiang,LIU Hanze,XIN Xiangpeng.Symmetry reductions,exact equation and the conservation laws of the generalized (3+1) dimensional Zakharov-Kuznetsov equation[J].Journal of Physics,2017,66(8):1-7.