基于柔性电磁传感器的发动机叶片微缺陷检测

陈棣湘，潘孟春，田武刚，周卫红，谢瑞芳

（国防科技大学智能科学学院，湖南 长沙 410073）

0 引 言

发动机叶片是飞机的关键部件，具有不规则的曲面结构，由于长期工作在高温、高压、高速的条件下，疲劳裂纹造成突然断裂而失效的现象时有发生，严重威胁飞机的飞行安全[1]。目前，无损检测技术（如常规涡流、磁粉、渗透和射线等）因其技术上的局限性，难以实现复杂结构中缺陷的定量检测[2-6]。田贵云等[2-3]将脉冲涡流检测技术应用于工件中隐藏缺陷的检测，通过对脉冲涡流信号的频谱分析和脉冲涡流成像，取得了良好效果，但在微缺陷的检测分辨力方面仍有待进一步提高。近年来，很多学者尝试将平面阵列式涡流传感器应用于复杂形状部件的无损检测，在平面阵列式涡流传感器的工作原理、结构设计、柔性化制造和参数标定等方面开展了广泛研究[4-6]，极大推动了该技术的发展与应用。但针对平面阵列式涡流传感器的信号处理问题，却鲜有报道。事实上，由于微缺陷导致的涡流场扰动很小，而平面涡流传感器激励线圈和检测线圈的匝数由于受结构的限制而非常有限，因此能够获取的感应电压信号及其变化量通常都很微弱，很容易被提离（传感器与检测对象之间的间隙）等干扰淹没。因此，平面涡流传感器的高精度信号检测非常关键，直接影响检测效果。本文针对飞机发动机叶片缺陷定量检测难度大、效果差、效率低的问题，建立了一种基于柔性电磁传感器的缺陷定量检测方法。

1 柔性电磁传感器

电磁无损检测技术具有传感器响应速度快、灵敏度高等优点，是对装备关键部件微损伤进行检测的有效方法之一。但是，传统的电磁无损检测系统普遍存在传感器一致性差、与被测对象贴合不好、检测信号易受提离（传感器与被测对象的间隙）等问题，使其应用受到了限制。采用平面阵列式柔性电磁传感器可望解决这一问题。

平面阵列式电磁传感器的结构如图1所示。这种传感器具有空间周期性结构，传感器的初级绕组在激励电流的作用下将产生空间周期性的电磁场，在被测材料中产生空间周期性的涡流场，并在其两侧的两个次级绕组的端部感应出极性相反的电压；当被测材料中存在缺陷时，次级绕组中的感应电压就会发生变化，据此可以检测出缺陷。图中ID为流过初级绕组的激励电流，VS1、VS2为次级绕组输出的感应电压，H为磁场强度，λ为传感器的空间波长，MUT为被测材料。该传感器的绕组模式有利于提高激励磁场的均匀性和传感器的检测灵敏度，并允许对多层介质与初级绕组产生的周期性电磁场的相互作用进行准确建模，从而大大降低校准要求[7-8]。

平面阵列式电磁传感器由于采用单层线圈结构，可以方便地制作在柔性基底上，自动适应被测对象形状的变化，极大增强使用的灵活性。这非常有利于检测发动机叶片这种不规则曲面结构。

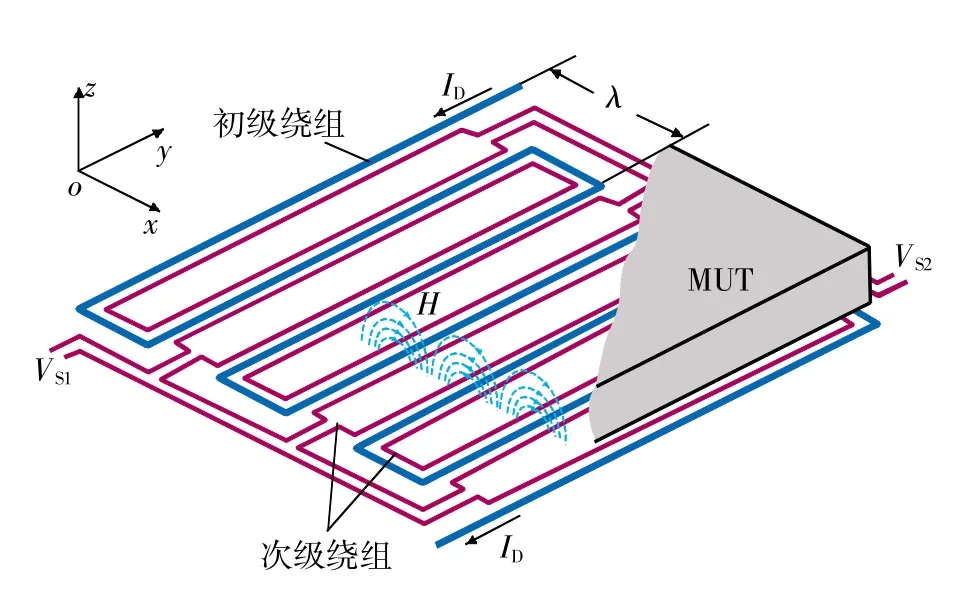
图1 平面电磁传感器阵列结构示意图

2 转移阻抗及其测量方法

2.1 转移阻抗的概念

平面电磁传感器的转移阻抗Z定义为次级绕组输出的感应电压VS与初级绕组的激励电流ID之比，即：

当激励电流保持恒定时，若被测材料中存在缺陷，次级绕组输出的感应电压将会发生变化，导致传感器的转移阻抗也会发生相应的变化。因此，通过转移阻抗的测量，就可以实现缺陷的检测。

2.2 转移阻抗的测量方法

由于平面阵列式电磁传感器的输出信号很微弱，为提高测量精度，采用了数字锁定检测算法对其进行测量。

假设激励电流的幅度为1，初相位为0，频率为fr，传感器输出的感应电压可用下式表示：

式中：A——幅度；

φ——初相位。

当采样频率为信号频率的N倍时（N＞2），若连续采样M点，可得到采样序列：

数字锁定放大器中所需的正弦和余弦参考序列rs（k）和rc（k）可分别表示为

式（3）～式（5）中，k=0，1，2，…，M-1。

将正弦和余弦参考序列分别与采样序列x（k）进行数字相关运算，可得：

因此，感应电压的幅度和初相位可分别根据下面两式计算得到：

由于激励电流的幅度为1，初相位为0，因此计算得到的A和φ也即传感器转移阻抗的幅度与相位[9]。

3 检测系统与实验

3.1 检测系统

检测系统总体结构如图2所示。可以看出，检测系统由传感器、多路阻抗精密测量电路、微损伤定量检测方法和信息处理平台4大部分构成。激励信号由FPGA芯片控制DDS电路产生，经功率放大后，在柔性阵列式电磁传感器的初级绕组中产生激励电流，从而在被测导电材料中产生涡流场。缺陷的存在会对涡流场的分布产生扰动，并导致传感器次级绕组输出的感应电压发生变化。阵列传感器输出的多路感应电压经信号调理、通道控制和数据采集后，进入数字锁定放大器进行处理 （数字锁定检测算法中所需的正弦和余弦参考序列由FPGA芯片产生），获得检测信号的幅度和相位信息，再根据确定幅度和相位的激励电流就可以计算出传感器的转移阻抗，经标定后采用多变量非线性搜索和插值算法从测量网格（根据检测模型事先建立的数据库，反映了转移阻抗与材料属性的对应关系）中准确获取材料的电导率、磁导率等物理属性[10]，在此基础上完成缺陷定量检测、残余应力检测和缺陷实时成像。信息处理平台以ARM为核心，主要用于算法实现并完成检测参数设置、检测结果输出等人机界面功能。

3.2 检测实验

在激励信号频率为2 MHz的情况下，首先测量传感器不与试块接触（位于空气中）时8通道的转移阻抗值。在5min内通过连续测量得到了600组数据，计算得到转移阻抗幅度与相位的均值和标准差如表1所示。

保持传感器工作频率不变，固定传感器使之紧贴铝合金试块，其中检测通道1所对应的检测线圈处于长1mm、宽0.1mm、深1mm槽形裂纹的正上方，其他检测线圈下方无缺陷；测量传感器各检测通道的转移阻抗值，并计算其均值与标准差，结果如表2所示。

从表1和表2的实验数据可以发现，传感器不与试块接触时转移阻抗幅度测量的重复精度（标准差与均值之比）约为0.04%，相位测量的重复精度约为0.02%；传感器紧贴试块时，由于电导率增大、提离减小，转移阻抗幅度下降、相位减小。

图2 检测系统总体结构

表1 传感器不与试块接触时转移阻抗的均值与标准差

表2 传感器紧贴试块时转移阻抗的均值与标准差

表3 传感器不与试块接触和传感器紧贴试块时阻抗比较表

将传感器不与试块接触和紧贴试块两种情况下各通道的转移阻抗幅度相除、相位相减，得到的幅度比例和相位差如表3所示。

从表3可以看出，当传感器紧贴试块时，由于缺陷处较无缺陷处电导率小、提离大，因此检测通道1（对应的检测线圈位于缺陷上方）的转移阻抗幅度和相位的变化量（表3第1列）都比其他通道要小，差别大于20%，据此就可以检测出缺陷，并实现裂纹长度的定量[11-12]。

4 结束语

平面阵列式柔性电磁传感器具有一致性好、与被测对象紧密贴合等优点，可有效提高检测精度，并抑制提离对检测结果的影响。采用数字锁定检测算法，使传感器转移阻抗幅度测量的重复精度达到0.04%，相位测量的重复精度达到0.02%；搭建了精密阻抗测量系统，通过对传感器不同工作条件下转移阻抗幅度变化比例和相位差的分析，可有效检测出0.1mm宽度的微缺陷。

[1]许占显，林为干.飞机发动机叶片裂纹的交变磁场非接触原位探测[J].无损检测，2005，27（12）：637-639.

[2]TIAN G Y，HE Y，ADEWALE I，et al.Research on spectralresponseofpulsed eddy currentand NDE applications[J].Sensors and Actuators A： Physical，2013（189）：313-320.

[3]HE Y，PAN M，LUO F，et al.Pulsed eddy current imaging and frequency spectrum analysisforhidden defect nondestructive testing and evaluation[J].NDT&E International，2011（44）：344-352.

[4]ROSADO L S，GONZALEZD J C，SANTOSD T G，et al.Geometric optimization ofa differentialplanareddy currents probe for non-destructive testing[J].Sensors and Actuators A:Physical，2013（197）：96-105.

[5]LEPAGE B.Development of a flexible cross-wound eddy current array probe[J].International Journal of Applied Electromagnetics and Mechanics，2014（45）：633-638.

[6]LIM Y Y，SOH C K.Electro-mechanical impedance（EMI） -based incipientcrack monitoringand critical crack identification of beam structures[J].Research in Nondestructive Evaluation，2014（25）：82-98.

[7]ZILBERSTEIN V，EVANS L，HUGUENINL C，et al.Quality assessment of refractory protective coatings using multi-frequency eddy current MWM-arrays[J].Review of Quantitative Nondestructive Evaluation，2006（25）：1067-1074.

[8]SHEIRETOV Y，GRUNDY D，ZILBERSTEIN V.MWMArray sensors for in situ monitoring of high-temperature components in power plants[J].IEEE Sensors Journal，2009，9（11）：1527-1536.

[9]沐阿华，张磊.基于DAQ和数字锁定技术的微弱信号测量仪的设计与实现[J].测控技术，2013，32（10）：16-20.

[10]贺红娟，陈棣湘，赵建强，等.用于微损伤定量评估的多变量非线性插值算法[J].传感技术学报，2012，25（12）：1696-1700.

[11]XIE R F，CHEN D X，et al.Fatigue crack length sizing using a novel flexible eddy current sensor array[J].Sensors，2015（15）：32138-32151.

[12]CHEN D X，XIE R F，ZHOU W H，et al.Multichannel transimpedance measurement of a planar electromagnetic sensor array[J].Measurement Science and Technology，2015（26）：025102.