水中超高速射弹可压缩空泡流研究进展

贾林利，要 尧，蒋运华

（1.黑龙江工程学院 机电工程学院，哈尔滨150001；2.哈尔滨工程大学 航天工程系，哈尔滨 150001）

0 引 言

由于水介质阻力较大，传统的水下航行和推进技术很难突破80节的极限。超空泡技术主要通过低压汽化和人工通气的共同作用，在运动体周围形成一个气泡并将其包裹，降低摩擦阻力，从而使鱼雷、潜艇、船舶及水雷等大尺度水中运动体的速度提高到100 m/s以上。对于小尺度的超空泡射弹则能突破水中音速（1 450 m/s），实现水中超音速航行[1-2]。水中超音速航行的实现，将会拥有类似空气中突破音速一样的经济及军事价值。与大尺度的超空泡运动体相比，水中超音速航行必须开展水中高速可压缩流研究。本文首先分析了国内外水中亚音速、跨音速及超音速流动空泡形状计算及空化阻力势流理论研究成果、超高速航行体结构研究现状；然后，综述了水中超高速的水、蒸汽、空气多相混合可压缩流数值计算方法的研究进展，及需要解决的关键问题；最后，重点介绍了乌克兰和美国水中亚音速、跨音速及超音速水中试验的研究方法、研究成果及研究趋势。

1 水中超高速可压缩流理论研究

从1980年以后，前苏联和美国开始关注水中可压缩流。Aleve[3-4]开展了关于轴对称物体以亚/跨/超音速进入，并在水中运动的非线性数值预测方法研究。Frolov[5]基于Burago方法提出一种考虑了可压缩性影响，既可用于空化流，也可用于连续流的计算模型。这种方法对空气中的二维可压缩流动有较好的预测，文中将这种方法应用到水中轴对称流并与空气中的流动计算结果进行比较，认为对二维外形，可压缩性的影响要比轴对称的大。Mayboroda[6]研究了有限大小的平板以亚音速及超音速在水面滑行时的升力及阻力计算方法。Zigangareva[7-8]研究了亚音速轴对称有限长度超空泡流非线性解析数值方法。 Yakimov[9]，Vasin[10]，Serebryakov[11]和 Nesteruk[12]从细长体理论出发，研究了水中可压缩流动，并且获得了一些相似的结论。安伟光等[13-16]基于概率及非概率法研究了跨音速及超音速航行体结构的稳定可靠性问题。这些理论研究中，对于可压缩空泡流的空泡形状、空化阻力，以Vasin，Serebryakov和Nesteruk的工作最为突出。

Serebryakov[10，17-21]应用细长体理论，对水中亚音速及超音速可压缩流进行了分析和计算，给出了基于细长体理论的线性一阶二阶近似计算方法。基于细长体理论线性近似分为两种情况讨论，一是细长空化器后的细长空泡，这种情况，空泡的长度和空化器的长度为相同的量级；二是类似于圆盘这样的非细长空化器后的空泡问题。对于细长空化器的细长空泡，空泡计算由一个外部区域组成。依据细长体理论获得的积分微分方程及空泡线性化，如下[17]：

一阶近似获得M＜1、M＞1时的计算公式为[18]

二阶近似获得σ为常值时的计算公式为：

对于小空化器后的细长空泡，这是实际可能应用的超空泡流动。它的空泡计算分成三个区域，1是空化器附近的解，2是连接1和3部分的解，3是外部解。外部解为空泡的最大部分，忽略空化器的尺寸并假定空泡的半长 Lk=1，对于 σ 为常值，当 （σ/δ2ln（1/δ2）→1 ）时有如下的解[19]：

当空化数为零，从积分微分方程中获得第2部分解的方程如下：

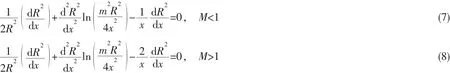
非细长圆盘形空化器，第一部分的解是非线性的，对于M＜1可以获得一个不是很严格，但且有效的解。计算表明，对于空泡前部，当M＜1，可压缩性影响不大，当M＞1，空泡前部要比M＜1的窄。

Serebryakov[20]还考虑了在M＜1、M＞1时壁面及自由边界到空泡轴为小距离的情况，壁面和边界的影响。研究表明，壁面对流动的影响主要体现在，增加流动的惯性和增加跨音速效应，而自由边界主要降低流动的惯性特性和完全抑制跨音速效应的影响。对于估算空化阻力可以用如下的表达式，对于圆盘有[20-21]

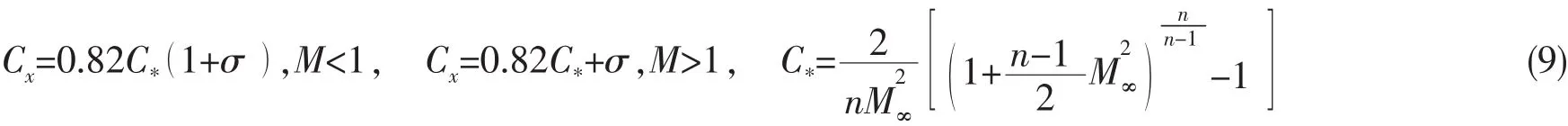
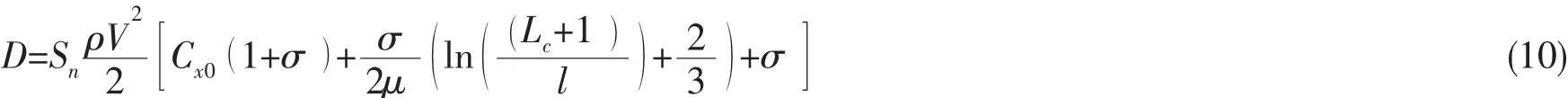
Vasin[22-25]基于细长体理论，获得细长圆锥空化器空泡形状的一阶及二阶解，一阶解如（13）式，对于亚音速流动二阶解与一阶解的结果相差不大，都为椭圆形空泡。对于超音速流，一阶近似解与亚音速一致，二阶近似解获得一个与理论不一致的凹空泡形状。

细长空化器，对于M＜1，稳态情况下有

忽略空化器尺寸，可以获得亚/超音速空泡形状及空化数与马赫数、长细比之间的关系：

研究表明，在亚音速流动中可以忽略马赫数对空泡形状的影响，即空泡形状可以像不可压流中一样为一椭圆形。

Vasin[26-28]研究了水中超音速的激波问题，对于法向激波，考虑水中的质量、动量、能量方程及Tait方程，计算认为，绕楔形或圆锥的超音速流动，水中的临界角要比空气中流动的小得多。在压力小于3×103MPa时，Tait方程如下：

在压力大于3×103MPa时，

Nesteruk[11]基于细长体理论研究了水中超音速，获得二阶近似解，计算结果表明亚音速和超音速的可压缩性对空泡形状的影响不大。压缩性的影响主要体现在Cx0，对于圆锥空化器，亚音速及超音速有

基于细长体理论线性化，对水中亚/超音速流空泡形状及空化阻力的计算，已经获得了一些解[29]。理论研究认为水中流体可压缩性对空泡形状的影响不大，可压缩性影响主要体现在空化阻力上面。这些理论在一定程度上能揭示一些水中亚音速和超音速可压缩流动的现象，但势流理论存在固有的缺陷。水中的跨音速区域相比于空气较宽，目前，跨音速区域方面的理论研究极其缺乏，没有获得有效的计算方法。所以应该研究给出计算跨音速区的空泡形状，最大直径，长度及空化阻力的有效计算公式，并依照试验结果来验证和修正这些理论。

2 水中超高速可压缩流数值研究

流体和汽液混合相的可压缩性对超空泡流的影响主要体现在三个方面，一是，低速空化流混合相的声速比液体和气体的声速都小，因此混合相包含可压缩流动；二是，对于水下高速运动体的火箭发动机的喷气速度为超音速；三是，高速射弹，它能超过当地的水中声速。

美国宾夕法尼亚州立大学的应用研究实验室，以Kunz[30-31]为代表的学者，对通气及自然空泡流的数值方法开展了大量有效的研究，并开发了计算代码UNCLE-M。它采用了预处理时间行进算法来计算多相流。最近又在该代码的基础之上考虑水的可压缩性，但是考虑可压缩性时，只将密度考虑成压力的函数，与温度无关，所以不考虑能量方程。计算了等温可压多相超音速流激波特性。数值计算了M=1.03的射弹，计算表明在射弹表面的液体将在射弹下游尾流中完全被蒸汽化，并能明显观察到激波现象，计算结果见图1，但对于该计算方法中的具体模型试验条件、数值计算参数及边界条件等细节问题没有给出[32-35]。

Vasin[36-37]对Riabouchinsky闭合形式的可压缩超空泡轴对称流进行了计算，运用有限差分法计算，一般情况，迭代解不满足空泡表面不可穿透的边界条件 ，因此二次迭代针对空泡形状，这样获得的解满足常值速度和不可穿透条件。计算表明，速度超过音速后，空泡形状没有发生实质性的改变，依然为接近椭圆形，马赫数主要影响空化器的阻力。控制方程及密度速度关系为：

图1 Kunz的数值计算结果与试验对比Fig.1 The comparison of Kunz’s computational results and tests

Schaffar[38]应用求解连续介质的冲击及爆炸问题和两相流模型计算了水中700到1 800 m/s流动状况，并对两种方法进行了对比研究。对于两相流模型，该模型基于两相温度平衡，即蒸汽化是瞬时的，给出两种流体的状态方程，并考虑守恒形式 ρ，ρu，ρv，ρE，的微分方程，迭代求解 αl，αv，ρ，p，u，v，T。对于求解连续介质的冲击及爆炸模型，使用OTi-HULL代码。文中用这两种方法对三个物体进行计算，三个物体的外形分别为头部圆锥角为45°，30°和15°，然后是圆柱段，最后是45°锥段闭合，并且头部为 45°，30°和 15°的物体的长度和质量分别为 3 cm，95 g；6 cm，265 g；6 cm，164 g，运动体的航行速度为3 000 m/s。

经过计算，两种计算方法获得的空泡外部的密度及压力分布具有相同的量级，空泡内部，由于OTi-HULL代码没有考虑低压的相变过程，所以它的计算结果明显是错误的；对于两相流计算，空泡随着头部圆锥角减小而减小，这个结果也是不期望出现的。对于空泡外形的计算，两种计算方法的结果之间的差别随着头部圆锥角的减小而增大。实际上对于这两种方法的计算结果应该与试验结果进行对比研究，但目前这方面的试验没有看到公开发表。

van der Heul[39]考虑无粘等温流动，运用可压缩修正的方法求解正压均匀空化流模型，模拟了NACA66空化特性。Ahuja[40-41]考虑混合相的连续方程、动量方程、汽相输运方程、高雷诺数k-ε湍流方程及渐进壁面模型，考虑壁面附近的低雷诺数效应，应用该空化模型计算半球圆柱及NACA66水翼不同空化数下的稳定层状空化流动，计算结果压力曲线与试验结果吻合。Saurel[42]研究了高速射弹尾迹的空化，基于Euler方程给出两相混合模型，依据可压缩流体、可压缩两相混合、可压缩蒸汽的状态方程闭合数学模型。求解该模型并与有解析解的一维模型对比，证明有效性。对于超高速水下射弹，该模型能计算不稳定激波的发展及射弹尾迹的空化发展区。Schnerr等[43]利用理想气体描述汽相状态方程，Tait方程描述液相的状态方程，并定义混合状态方程。数值求解包含能量守恒非稳态可压缩Euler方程，模拟了NACA0015水翼空化流、2D及3D的喷管的激波特性，三维弯曲水翼的空化特性。

鲁传敬[44]考虑密度和粘度都将发生变化，对跨声速来流的高速空化流动进行了计算。液相密度ρl由依据试验p、V、T关系数据拟合得到的带温度修正的Tait方程描述，蒸汽相密度ρv为常数，或由Peng-Robinson状态方程计算。张鹏[45]在Fluent 6.3的Mixture模型下利用不含温度影响Tait方程对密度修正，并与不修正的结果进行比较，认为跨超音速下，水的可压缩性会增加射弹的阻力；另外，采用可压单相流计算射弹周围温度场的分布，认为射弹高速运动会产生大量的热。贾力平[46]通过完全气体状态方程建立汽相密度随压力的变化关系，给出混合相密度及汽相输运方程中的源相表达式，计算了等温多相通气流动的可压缩效应。易文俊[47-49]基于Rayleigh-Plesset单一介质可变密度混合多相流模型，计算了高速射弹模型的空泡外形及阻力特性，控制方程中没有考虑可压缩性的影响。

数值模拟水的可压缩性的研究并没有获得很好的解决，多数学者主要考虑了混合相可压缩性的声学效应，给出了混合相可压缩性效应的数值模拟方法。考虑水的可压缩性的研究才刚刚起步，认为水为等温过程，密度只与压力有关，不涉及温度和能量方程。考虑全可压的大密度比的混合多相流动，将是数值预测超音速空泡流动遇到的关键技术问题。

3 水中超高速可压缩流试验研究

目前，主要有乌克兰国家科学院流体力学研究所（IHM）和美国海军水下作战中心（NUWC）对水中亚/超音速开展了相关的试验研究。

Savchenko[1，50]，Vlasenko[51]，提到IHM有关水中高速射弹的试验研究。描述了在IHM用于研究水中亚/超音速流的发射箱。该发射箱的尺寸为35 m长，横截面为2.2×2.2 m，它有10对观察孔，发射装置用压缩气体或电化学弹射器。并给出了试验用的射弹模型（见图2（a）），它由射弹1和容器2，并且容器2由两瓣在橡胶环3和头部金属盖4组装。模型材料为钢和钛，直径为10～17 mm，空化器直径为1.2～3 mm。

测量方法主要为高速相机，试验速度范围为V=500～1 400 m/s，这种流动的主要特征为大长细比λ=70～200。文献给出了空化器直径为1～3 mm试验速度范围为V=575～1 100 m/s的高速照片，认为可压缩性的影响仅限于空化器直径量纲范围的区域。将试验获得的空泡长度及直径的数据与Garabedian的渐进公式及空化数为0.01～0.06试验拟合公式进行比较，发现这些公式计算所得的结果与试验结果相差不大。图2（b）给出了超音速试验图片，该试验的发射装置为电化学弹射器。环境参数为：水温4℃；声速а=1 422 m/s；发射深度h=0.5 m；模型参数为：空化器直径2 mm；射弹长度85 mm；测量装置，拍摄频率25 000 Hz，网格刻度为50 mm；射弹速度V=1 550 m/s，M=1.09。在试验照片上能清楚看到射弹高速运动产生的前后激波。在试验研究后，指出高速射弹的两种稳定机制，一是射弹与空泡壁相互作用稳定，另外一种是射弹与空泡内的蒸汽射流介质相互作用稳定。

图2 IHM试验用射弹模型及试验照片Fig.2 The projectile model and test photos for IHM tests

NUWC为了研究水中超音速问题，研发了一套试验装置[52]。该装置包含如下的子系统：（1）水下发射系统，它长3.05 m，30 mm膛孔，发射枪安装在一个盒状的框上，这个框有通过上下两对轨道与一个外框相连，内框上还安装有一个钢板，它主要用于增加阻尼，使内框快速停止运动；（2）枪口闸门系统，主要为了减少燃烧气体进入空泡；（3）射弹围堵系统，该系统主要用于保证试验的安全；（4）计算机数据采集系统，该系统由两个高速数据记录平台组成，同时每个平台还有两个类似的定时器和数据通道，用于触发相机等其它的测试仪器；（5）发射压力及出膛速度系统；（6）速度测量及触发系统，可以用一个磁化的射弹穿过两个自感应镀锡卷板，这样可以产生感应电压来测量速度或触发其它测试仪器。另外当射弹不是钢材，不能磁化时，可以用柔性聚酯薄膜组成闭合电路，来测量速度或触发其它测试仪器，同时，还可以依据不同位置的薄膜的穿孔位置及形状来记录射弹的弹道；（7）相机、传感器的围栏及支撑系统，主要为了保证相机及传感器安装到指定的位置，并能安全的测量；（8）图像数据采集系统，标准的录像机，高速录像机（10 000帧/s）。

NUWC试验用射弹与IHM的射弹类似，见图3（a）。图3（b）为1 549 m/s试验照片，从该照片上可以清晰地看到水中前部激波的形状。

图3 NUWC试验用射弹模型及试验照片Fig.3 The projectile model and test photos for NUWC tests

熊天红[53]研究了射弹在500～900 m/s之间的不同空化器直径和不同长细比对射弹阻力的影响。

水中超音速试验在美国和乌克兰已经获得成功，并且他们开展了大量的亚音速、跨音速的试验研究。但涉及到亚音速、跨音速及超音速空泡流动的空泡形状、空化阻力计算和超音速下的激波特性，甚至有关试验条件及试验模型尺寸等具体问题公开发表的极少。

4 结 语

基于细长体理论，获得了水中亚音速和超音速流空泡形状、空化阻力的计算方法。理论研究认为水中流体可压缩性对空泡形状的影响不大，可压缩性影响主要体现在空化阻力上面。这些理论在一定程度上能揭示一些水中亚音速和超音速可压缩流动的基本现象。水中的跨音速区域要比空气中的宽，对于水中跨音速区域流动的空泡形状，最大直径，长度及空化阻力的有效计算公式还有待研究。

数值模拟方面，多数学者主要考虑了混合相可压缩性的声学效应，给出了混合相可压缩性数值模拟方法。目前，考虑水的可压缩性，认为水为等温过程，密度只与压力有关，不涉及温度和能量方程的数值模拟方法有一些成果，但是这些数值方法还有待完善。考虑全可压的大密度比的混合多相流动，是数值预测超音速空泡流动一个急需解决的关键问题。

理论研究及数值计算的有效性都有待试验的证实和修正，同时要成功实现水中高速可压缩流动实验室研究，也存在较大的困难。水中超音速试验在美国和乌克兰已经获得成功，但涉及到亚音速、跨音速及超音速空泡流动的空泡形状、空化阻力计算和超音速下的激波特性等关键问题的研究成果极少公开发表，所以，有必要系统地试验研究水中可压缩空泡流动的机理。

[1]Savchenko Yu N.Perspectives of the supercavitation flow applications[C]//International Conference on Innovative Approaches to Further Increase Speed of Fast Marine Vehicles,Moving Above,Under and in Water Surface,Super FAST’2008,July 2-4,2008.Saint-Petersburg,Russia,2008.

[2]刘 桦,李家春,何友声,孟庆国.‘十一五’水动力学发展规划的建议[J].力学进展,2007,37(1):142-147.Liu Hua,Li Jiachun,He Yousheng,Meng Qingguo.Suggestion on the research frame programme on hydrodynamics for the eleventh five-year plan[J].Advances in Mechanics,2007,37(1):142-147.(in Chinese)

[3]Aleve G A.Separating flow of circle cone by transonic flow of water[J].Trans.of AS USSR,MFG,1983(1):152-154.

[4]Aleve G.3-D problem of disc entering in compressible fluid[J].Trans.of AS USSR,MFG,1988(1):17-20.

[5]Frolov V A.High-speed compressible flows about axisymmetric bodies[C]//Cav03-OS-7-004,Fifth International Symposium on Cavitation(CAV2003),November 1-4,2003.Osaka,Japan,2003.

[6]Mayboroda A N.Planing for the sub-and supersonic speeds[C]//Cav03-OS-7-009,Fifth International Symposium on Cavitation(CAV2003),November 1-4,2003.Osaka,Japan,2003.

[7]Zigangareva L M,Kiselev O M.Subsonic cavitational flow by compressible fluid for small Cavitation Numbers[J],Trans RAN,1998(4):27-34.

[8]Zigangareva L M,Kiselev O M.Calculation of the compressible subsonic cavitation flow past a circular cone[J].Prikl.Mat.Mekh.,1994,58(4):93-107.(reprinted in the USA)

[9]Yakimov Yu L.Asymptotic laws of degeneration of thin cavity shapes[J].Izv.Akad.Nauk S SSR,Mekh.Zhidk.Gaza,1981(3):3-10.(reprinted in the USA)

[10]Serebryakov V V.Asymptotic solutions of axisymmetrical problems of subsonic and supersonic separated water flows with zero cavitation numbers[J].Dokl.Akad.Nauk Ukraine,1992(9):66-71.(in Russian)

[11]Vasin A D.Thin axisymmetric cavities in subsonic compressible flow[J].zv.Akad.Nauk SSSR,Mekh.Zhidk.Gaza,1987(5):174-177.(reprinted in the USA)

[12]Ihor Nesteruk.Influence of the flow unsteadiness,compressibility and capillarity on long axisymmetric cavities[C]//Cav03-GS-6-004,Fifth International Symposium on Cavitation(CAV2003),November 1-4,2003.Osaka,Japan,2003.

[13]安伟光,顾永维,安 海.初偏心影响下的水下高速运动体的抗弯稳定性及可靠性分析[J].兵工学报,2008,29(7):824-828.An Weiguang,Gu Yongwei,An Hai.Analysis of antibending stability and reliability of an elastic body with initial eccentricity at high speed motion underwater[J].ACTA Armamentari I,2008,29(7):824-828.(in Chinese)

[14]顾永维,安伟光,安 海.水下高速运动体的抗弯稳定可靠性分析[J].哈尔滨工程大学学报,2008,29(7):683-686.Gu Yongwei,An Weiguang,An Hai.Analyzing of buckling resistance of an underwate relastic body experiencing high speed motion[J].Journal of Harbin Engineering University,2008,29(7):683-686.(in Chinese)

[15]An Weiguang,Zhou Ling,An Hai.Structure buckling and non-probabilistic reliability analysis of supercavitating vehicles[J].Journal of Harbin Institute of Technology(New Series),2009,16(4):561-569.

[16]周 凌,安伟光,安 海.超空泡运动体强度与稳定性的非概率可靠性分析[J].哈尔滨工程大学学报,2009,30(4):363-367.Zhou Ling,An Weiguang,An Hai.Non-probabilistic reliability analysis of supercavitating vehicles based on structure strength and buckling[J].Journal of Harbin Engineering University,2009,30(4):363-367.(in Chinese)

[17]Serebryakov V V.Some models of prediction of supercavitation flows based on slender body approximation[C]//Fourth International Symposium on Cavitation,California Institute of Technology,June 20-23,2001.Pasadena,CA USA,2001.

[18]Serebryakov V V.Models of the supercavitation prediction for high-speed motion in water[C]//Proceedings of International scientific school‘High speed Hydrodynamics’,Jun.16-23,2002.(Invited lecture).Chebocsary,Russia,2002:71-92.

[19]Serebryakov V,Schnerr G.Some problems of hydrodynamics for sub-,trans-supersonic motion in water with supercavitation[C]//Fifth International Symposium on Cavitation(CAV2003),Cav03-OS7-015 November 1-4,2003.Osaka,Japan,2003.

[20]Serebryakov V,Schnerr G H.On the theory for subsonic,transonic and supersonic flows in water with supercavitation[C]//FM5S_12066,XXI International Congress of Theoretical and Applied Mechanics,August 15-21,2004.Warsaw,Poland,2004.

[21]Serebryakov V V.On methods for analysis of supercavitation in a high-speed motion in water:incompressible approximation[J].International Journal of Fluid Mechanics Research,2006,33(2):186-210.

[22]Vasin A D.Thin axisymmetric cavities in subsonic compressible flow[J].zv.Akad.Nauk SSSR,Mekh.Zhidk.Gaza,1987(5):174-177.(reprinted in the USA)

[23]Vasin A D.Application of the slender body theory to investigate developed axisymmetric cavitation flows in a subsonic stream of compressible fluid[J].Applied Hydromechanics,Kiev,2000,2(74):17-25.(in Russian)

[24]Vasin A D.Supercavities in compressible fluid[C].Paper presented at the RTO AVT Lecture Series on‘Supercavitating Flows’,held at the von Kármán Institute(VKI)in Brussels,Belgium,and published in RTO EN-016,12-16 February 2001.

[25]Vasin A D.The principle of independence of the cavity sections expansion(Logvinovich’s principle)as the basis for investigation on cavitation flows[C].Paper presented at the RTO AVT Lecture Series on ‘Supercavitating Flows’,held at the von Kármán Institute(VKI)in Brussels,Belgium,and published in RTO EN-08,12-16 February 2001.

[26]Vasin A D.Shocks and conical flows in a supersonic water stream[J]Izv.Rus.Akad.Nauk,Mekh.Zhidk.Gaza,1998(5):196-199.(reprinted in the USA)

[27]Vasin A D.High-speed body motion in compressible fluid[C]//In Proceedings of the Scientific Meeting on High-Speed Hydrodynamics and Supercavitation.Laboratoire des Ecoulements Geophysiques et Industriels.Grenoble,France,2000.

[28]VASIN A D.Some problems of supersonic cavitation flows[C]//The 4th International Symposium on Cavitation,20-23 June,2001.Pasadena,California,2001.

[29]张志宏,孟庆昌,金永刚,顾建农.超声速细长锥型射弹超空泡流动数值计算方法[J].华中科技大学学报(自然科学版),2014,42(1):39-43.Zhang Zhihong,Meng Qingchang,Jin Yonggang,Gu Jiannong.Numerical method of supercavitating flow past a slender cone type projectile traveling at supersonic speed[J].J Huazhong Univ.of Sci.&Tech.(Natural Science Edition),2014,42(1):39-43.(in Chinese)

[30]Kunz R F,Lindau J W,Billet M L,Stinebring D R.Multiphase CFD modeling of developed and supercavitating flows[C]//Paper presented at the RTO AVT Lecture Series on ‘Supercavitating Flows’,held at the von Kármán Institute(VKI)in Brussels,Belgium,and published in RTO EN-013,12-16 February,2001.

[31]Lindau J W,Kunz R F,Venkateswaran S,Boger D A.Application of a preconditioned,multiple-species,compressible,navier-stokes model to cavitating flows[C]//The 4th International Symposium on Cavitation,20-23 June,2001.Pasadena,California,2001.

[32]Lindau J W,Venkateswaran S,Kunz R F,Merkle C L.Development of a fully-compressible multi-phase Reynolds-averaged Navier-stokes model[C]//Submitted to the 15th AIAA CFD Conference,11-14 June,2001.Anaheim,California,2001.

[33]Venkateswaran S,Lindau J W,Kunz R F,Merkle C L.Computation of multiphase mixture flows with compressibility effects[J].Journal of Computational Physics,2002,180:54-77.

[34]Lindau J W,Venkateswaran S,Kunz R F,Merkle C L.Computation of compressible multiphase flows[C]//AIAA 2003-1285,41st Aerospace Sciences Meeting and Exhibit 6-9 January 2003.Reno,Nevada,2003.

[35]Lindau J W,Kunz R F,Venkateswaran S,Stinebring D R.Homogeneous multiphase CFD modeling of large scale cavities[C].European Congress on Computational Methods in Applied Sciences and Engineering ECCOMAS 2004,Neittaanmäki P,Rossi T,Korotov S,Oñate E,Périaux J,Knörzer D(eds.)Jyväskylä,24-28 July 2004..

[36]Vasin A D.Calculation of axisymmetric cavities downstream of a disk in subsonic compressible fluid flow[J].Izv.Rus.Akad.Nauk,Mekh.Zhidk.Gaza,1996(2):94-103.(reprinted in the USA)

[37]Vasin A D.Calculation of axisymmetric cavities downstream of a disk in supersonic flow[J].Izv.Rus.Akad.Nauk,Mekh.Zhidk.Gaza,1997(4):54-62.(reprinted in the USA)

[38]Schaffar M,Pfeifer H J.Comparison of two computational methods for high-velocity cavitating flows around conical projectiles:OTi-HULL hydrocode and two-phase flow method[C]//The 4th International Symposium on Cavitation.20-23 June,2001.Pasadena,California,2001.

[39]van der Heul D R,Vuik C,Wesseling P.Efficient computation of flow with cavitation by compressible pressure correction[C]//European Congress on Computational Methods in Applied Sciences and Engineering ECCOMAS 2000,11-14 September 2000.Barcelona,2000.

[40]Ahuja V,Hosangadi A,Arunajatesan S.Simulations of cavitating flows using hybrid unstructured meshes[J].Journal of Fluids Engineering,2001,123:331-340.

[41]Ahuja V,Hosangadi A,Ungewitter R,Dash S M.A hybrid unstructured mesh solver for mutli-fluid mixtures[J].1999,AIAA Paper 99-3330.

[42]Saurel R,Cocchi J P,Butler P B.Numerical study of cavitation in the wake of a hypervelocity underwater projectile[J].AIAA Journal of Propulsion and Power,1999,15(4):513-520.

[43]Schnerr G H,Schmidt S,Sezal I,Thalhamer M.Shock and wave dynamics of compressible liquid flows with special emphasis on unsteady load on hydrofoils and on cavitation in injection nozzles[C]//Sixth International Symposium on Cavitation CAV2006,September,2006.Wageningen,The Netherlands,2006.

[44]鲁传敬,陈 瑛.空泡流数值模拟方法研究[C]//第九届全国水动力学学术会议暨第二十二届全国水动力学研讨会文集,中国四川成都,2009.Lu Chuanjing,Chen Ying.Study of the numerieal method for natural cavitating flow[C]//Proceedings of Ninth National Conference on Water Dynamics and the Twenty-Second National Symposium on Water Dynamics.Chengdu,Sichuan,China,2009:54-65.(in Chinese)

[45]张 鹏,傅慧萍.跨超音速射弹的超空泡数值模拟[J].弹箭与制导学报,2009,29(5):166-169.Zhang Peng,Fu Huiping.The numerical simulation of supercavitation around projectiles from subsonic to supersonic[J].Journal of Projectiles,Rockets,Missiles and Guidance,2009,29(5):166-169.(in Chinese)

[46]贾力平.空化器诱导超空泡特性的数值仿真与试验研究[D].哈尔滨:哈尔滨工业大学,2007.Jia Liping.Numerical simulation and experimental study on supercavity characteristic induced by cavitators[D].Harbin:Harbin Institute of Technology,2007.(in Chinese)

[47]易文俊,李月洁,王中原,熊天红,钱吉胜.小攻角下水下高速射弹的空泡形态特性[J].南京理工大学学报(自然科学版),2008,32(4):464-467.Yi Wenjun,Li Yuejie,Wang Zhongyuan,Xiong Tianhong,Qian Jisheng.Characteristics of cavity shape for underwater high-speed projectile at small attack angle[J].Journal of Nanjing University of Science and Technology(Natural Science),2008,32(4):464-467.(in Chinese)

[48]易文俊,王中原,熊天红,周卫平.水下高速射弹超空泡减阻特性研究[J].弹道学报,2008,20(4):1-4.Yi Wenjun,Wang Zhongyuan,Xiong Tianhong,Zhou Weiping.Research on drag reduction characteristics of an underwater high-speed supercavitation projectile[J].Journal of Ballistics,2008,20(4):1-4.(in Chinese)

[49]熊天红,李铁鹏,易文俊,吴军基.水下高速射弹超空泡形态与阻力特性研究[J].弹道学报,2009,21(2):100-102.Xiong Tianhong,Li Tiepeng,Yi Wenjun,Wu Junji.Investigation on characteristics of cavity form and drag for underwater high-speed projectile[J].Journal of Ballistics,2009,21(2):100-102.(in Chinese)

[50]Savchenko Yu N.Experimental investigation of supercavitating motion of bodies[C]//Paper presented at the RTO AVT Lecture series on ‘Supercavitating Flows’,held at the von Kármán Institute(VKI)in Brussels,Belgium,and published in RTO EN-04,12-16 February,2001.

[51]Vlasenko Y D.Experimental investigation of supercavitation flow regimes at subsonic and transonic speeds[C]//Cav03-GS-6-006 Fifth International Symposium on Cavitation(cav2003),November 1-4,2003.Osaka,Japan,2003.

[52]Kirschner I N.Results of selected experiments involving supercavitating flows[C].Paper presented at the RTO AVT Lecture Series on ‘Supercavitating Flows’,held at the von Kármán Institute(VKI)in Brussels,Belgium,and published in RTO EN-015,12-16 February,2001.

[53]熊天红,易文俊.高速射弹超空泡减阻试验研究与数值模拟分析[J].工程力学,2009,26(8):174-178.Xiong Tianhong,Yi Wenjun.Experimental research and numerical simulation of supercavity drag reduction of a high speed projectile[J].Engineering Mechanics,2009,26(8):174-178.(in Chinese)