水下纵肋加强圆柱壳低频振动与声辐射

张 超 ， 商德江 ， 李 琪

（哈尔滨工程大学a.水声技术重点实验室；b.水声工程学院，哈尔滨150001）

0 引 言

圆柱壳采用肋骨加强，增强了结构抗压能力的同时，也在一定程度上改变了其水下振动与声辐射特性，因此，肋骨加强圆柱壳一直是水下结构振动声辐射研究的热点。肋骨有环肋和纵肋之分，目前国内外大量的研究集中于环肋加强圆柱壳[1-2]，对于纵肋加强圆柱壳的研究则相对较少，但是相关的研究也已逐渐开展。Ramachandran[3]采用统计能量法计算了纵向加强圆柱壳的模态密度、辐射效率和声响应，并与试验测量结果进行了比较。由于加肋后圆柱壳结构更加复杂，国内有人采用有限元结合边界元方法和计算加肋圆柱壳的振动与声辐射特性[4-5]，其中王路才[6]采用结构有限元耦合流体边界元的附加质量和附加阻尼算法，对具有不同数量纵桁的加筋环肋圆柱壳水下振动与声辐射噪声进行了数值计算，指出纵桁对水下圆柱壳具有较好的减振降噪效果，且纵桁数量越多减振降噪效果越好。另外，由于解析法具有物理概念清晰、易于揭示物理本质的优点，解析法也被多个学者采用。曾革委[7]研究了外壳板加纵骨的双层圆柱壳的水下声辐射问题，指出在较低频率段外壳板加纵骨使双层加肋圆柱壳水下辐射声压增大。谢官模[8]建立了采用环肋、舱壁和纵骨加强的无限长圆柱壳的水下声辐射模型，研究了其声辐射特性。廖长江[9]建立了有限长纵向加肋圆柱壳的振动与声辐射模型，分析了纵肋数目和损耗因子对圆柱壳辐射声功率和均方振速的影响。以上解析计算中，纵肋均被简化为Euler-Bernoulli梁，且仅考虑了纵肋对圆柱壳的径向作用，未考虑纵肋的对圆柱壳其它方向的作用，也未考虑纵肋的扭转运动。

鉴于目前纵肋对圆柱壳低频振动和声辐射机理的研究相对较少，且纵肋对加圆柱壳作用的解析建模忽略因素较多，本文对纵肋的建模进行了深入分析，采用Timoshenko梁理论建立纵肋的弯曲振动方程，同时考虑纵肋的轴向纵振动和扭转振动，建立了纵肋加强圆柱壳振动声辐射的解析计算模型，分析了低频段纵肋对圆柱壳振动声辐射的影响。

1 理论建模

1.1 圆柱壳振动声辐射建模

有限长纵肋加强圆柱壳模型及坐标系如图1所示。圆柱壳两端简支在半无限长刚硬圆柱障板上，内部真空，置于无限大理想水介质中。

图1 纵肋加强圆柱壳模型及坐标系Fig.1 Longitudinally stiffened cylindrical shell model and coordinate system

圆柱壳运动采用经典薄壳理论描述，将纵肋和外流体对圆柱壳的作用力表示为圆柱壳位移的函数并施加到圆柱壳上，采用模态叠加法建立纵肋加强圆柱壳计算模型。圆柱壳运动方程采用Flügge薄壳理论描述如下[10]：

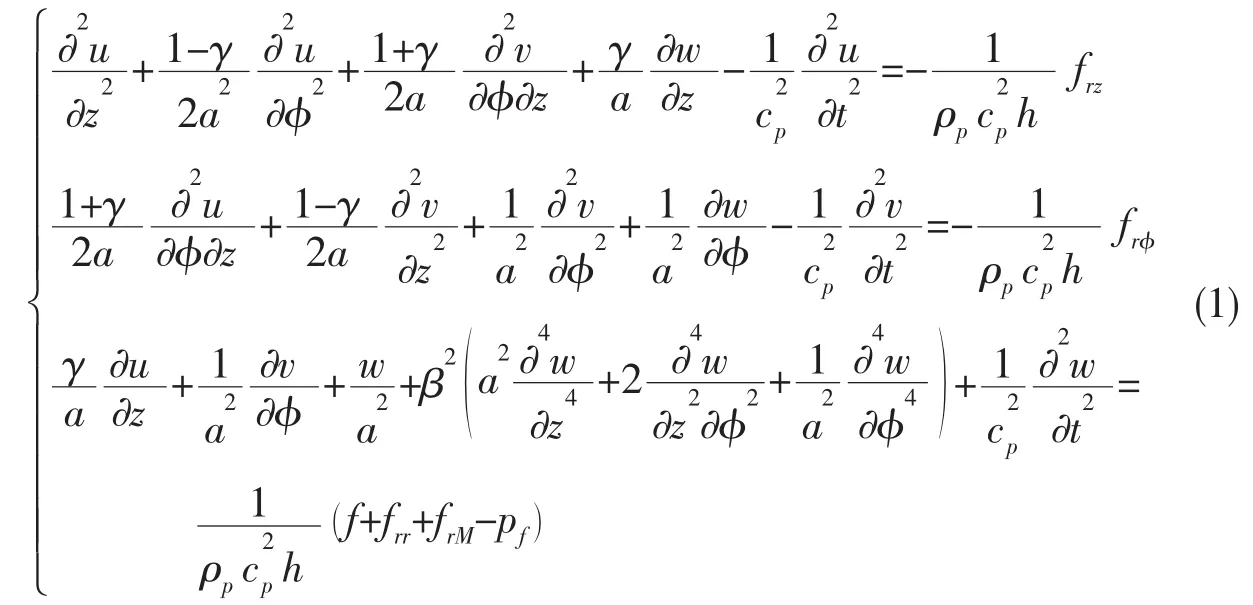
根据圆柱壳两端简支条件，圆柱壳位移可以表示为如下模态叠加的形式：

其中：km=mπ/L，L为圆柱壳轴向长度。对圆柱壳上各作用力也进行类似的模态分解，并连同（2）式代入（1）式可得：

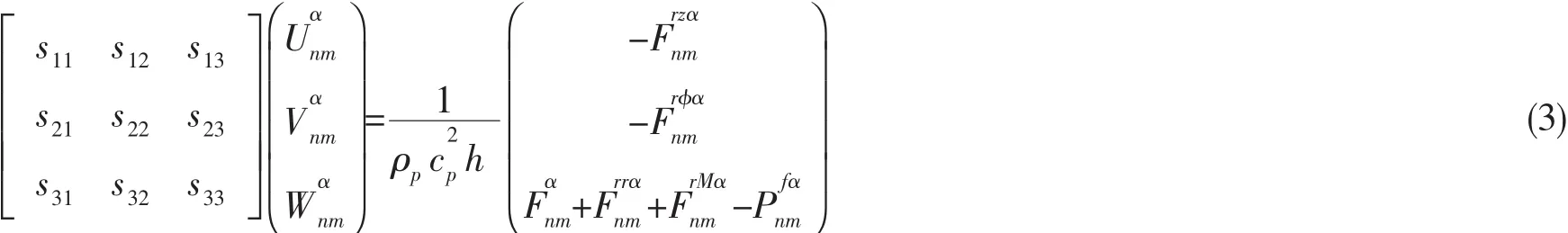
其中：sij为展开系数，为外激励力和外流体对圆柱壳作用力的模态展开系数，和分别为纵肋对圆柱壳各个作用力的模态展开系数。外激励力作用在圆柱壳面中心，其模态分解在诸多文献中都有描述[10]，不再赘述。外流体以作用反力的形式施加在圆柱壳上，其模态分解系数可写为[11]

当求得各作用力的模态展开系数（纵肋对圆柱壳作用力模态系数将在后面详细介绍）并代入（3）式可求得各位移模态系数，从而解得圆柱壳位移，代入外流体作用力公式，可求得圆柱壳表面声压，进一步结合圆柱壳表面位移一起可求得圆柱壳辐射声功率：

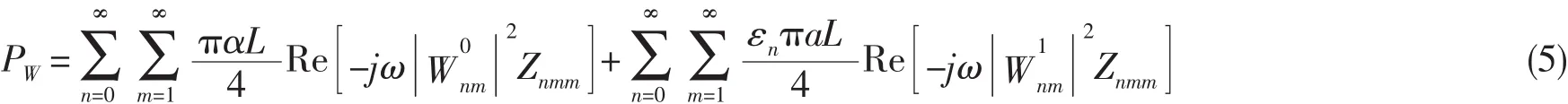
其中：Re表示取实部，ω 为角频率，n=0 时 εn=2，n≠0 时 εn=1。

经推导圆柱壳表面均方振速写为

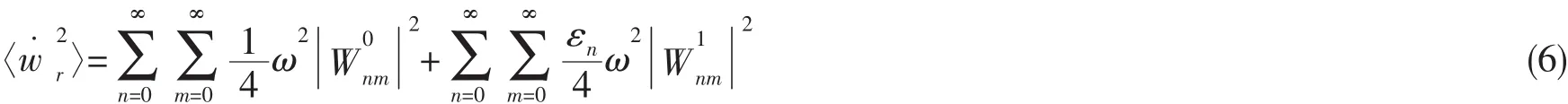
1.2 纵肋对圆柱壳作用建模

考虑纵肋的细长结构，纵肋往往被简化为梁，通常采用Euler-Bernoulli梁方程，仅考虑梁在圆柱壳中的径向振动，其运动方程如下：

其中：E、Ir、ρ和A分别为纵肋的杨氏模量、径向弯曲截面惯性矩、密度和截面积，分别为纵肋径向位移和所受的径向作用力。

实际上，纵肋的径向、周向弯曲、轴向纵振动以及扭转都会与圆柱壳产生相互作用力，这里充分考虑纵肋以上运动，且采用更严格的Timoshenko梁理论描述纵肋的弯曲运动，得到纵肋运动方程如下[12-13]：

其中：Iφ、Iω分别为纵肋的周向弯曲截面惯性矩、截面扇性惯性矩，Ip、J为截面极惯性矩、扭转常数，G为剪切模量，κ2为Timoshenko剪切系数为纵肋的周向、轴向位移以及扭转角和为纵肋受到的周向外力、轴向外力和扭转力矩。

设纵肋在圆柱壳的周向坐标为φr，在φ=φr处，纵肋与圆柱壳满足位移连续和相互作用力大小相等方向相反的边界条件：

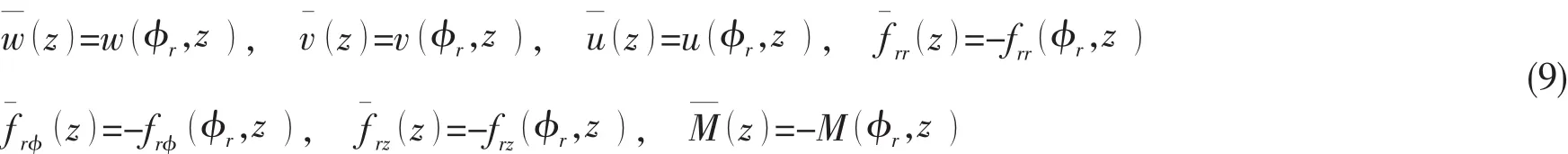
将（9）式代入（8）式，并考虑时间因子exp jω（）t和壳体位移展开函数式（2），可得：

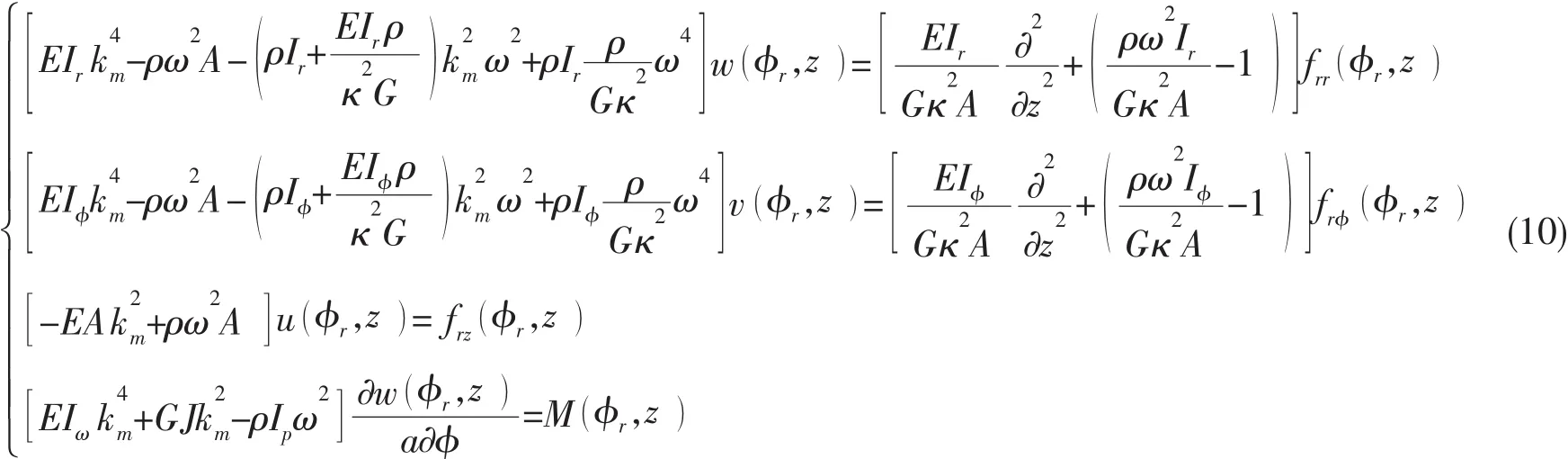
经推导，纵肋扭转引起的施加在圆柱壳上的径向力frM与纵肋反作用到圆柱壳上的弯矩M有如下关系：

其中：δ为Dirac函数。（9）式中各量均在φ=φr处成立，利用Dirac函数，可以得到：

综合（10）-（12）式，并代入（2）式即可得到纵肋对圆柱壳的各个作用力用圆柱壳位移u、v和w表示的形式，对其进行模态正交分解，即可求得各纵肋作用力模态系数和用圆柱壳模态位移系数和表示的形式，这里仅给出的计算结果，其它可类似地得出。

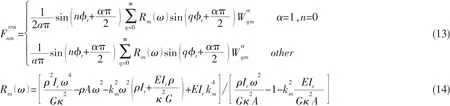
如有多条纵肋，可按上述方法，只需改变不同纵肋的位置φr，然后将不同位置纵肋的相应作用力系数累加即可。如果仅考虑纵肋的径向弯曲运动，由（7）式经过本文类似的推导，即可得到纵肋的传统简化梁计算方法。

2 建模计算分析

为验证本文理论建模的合理性，建立一水下纵肋加强圆柱壳模型，壳体参数如表1所示，周向均匀分布4条纵肋，壳体材料为钢。径向点激励力位于一条纵肋所在位置的圆柱壳面中心，幅值为1 N。

表1 纵肋加强圆柱壳模型参数Tab.1 Parameters of longitudinally stiffened cylindrical shell model

由于简支圆柱壳声辐射的解析计算已非常成熟[10-11]，这里仅从振动响应的角度对模型进行验证。分别采用ANSYS有限元法和不同简化的解析法，计算激励点处的振动响应并进行比较，如图2所示，其中ANSYS有限元法采用shell63单元和beam4单元进行建模。可以看出，采用Euler-Bernoulli理论仅考虑纵肋径向弯曲运动的传统建模方法，能基本反应纵肋对圆柱壳的作用，但是未计及轴向纵振动等其它振动模式，会产生不同程度的频率计算偏差。改用Timoshenko理论，以及再同时计及纵肋的周向弯曲运动，在研究频段内解析计算结果没有明显改善。同时考虑纵肋径向和周向弯曲以及轴向纵振动时，解析计算结果有明显改善，但是依然存在一定的频偏误差，当同时考虑纵肋径向弯曲以及轴向纵振动及扭转时，解析计算结果有更进一步的改善，当同时考虑纵肋的各种作用力后，解析解与有限元解吻合最好。因此，在研究频段内，纵肋的径向弯曲是最主要的，但是轴向纵振动和扭转振动会显著影响到计算结果的频率偏移，对于更精确的计算，则需同时考虑纵肋各个方向的作用力。对于辐射声功率的分析如图3所示，可见，纵肋的传统建模方法能够反映纵肋加强圆柱壳辐射声功率的基本趋势，但是在低频段差别较大，出现了明显了频偏误差，在更高频段上，无阻尼时，部分辐射峰频率及幅值计算误差也比较明显，加入阻尼后，误差稍小但依然存在。因此，纵肋径向弯曲之外的其它振动模式对圆柱壳的谐振峰频率及幅值也存在一定的影响，在要求更精确计算时，尤其在低频段，应采用本文综合建模方法。

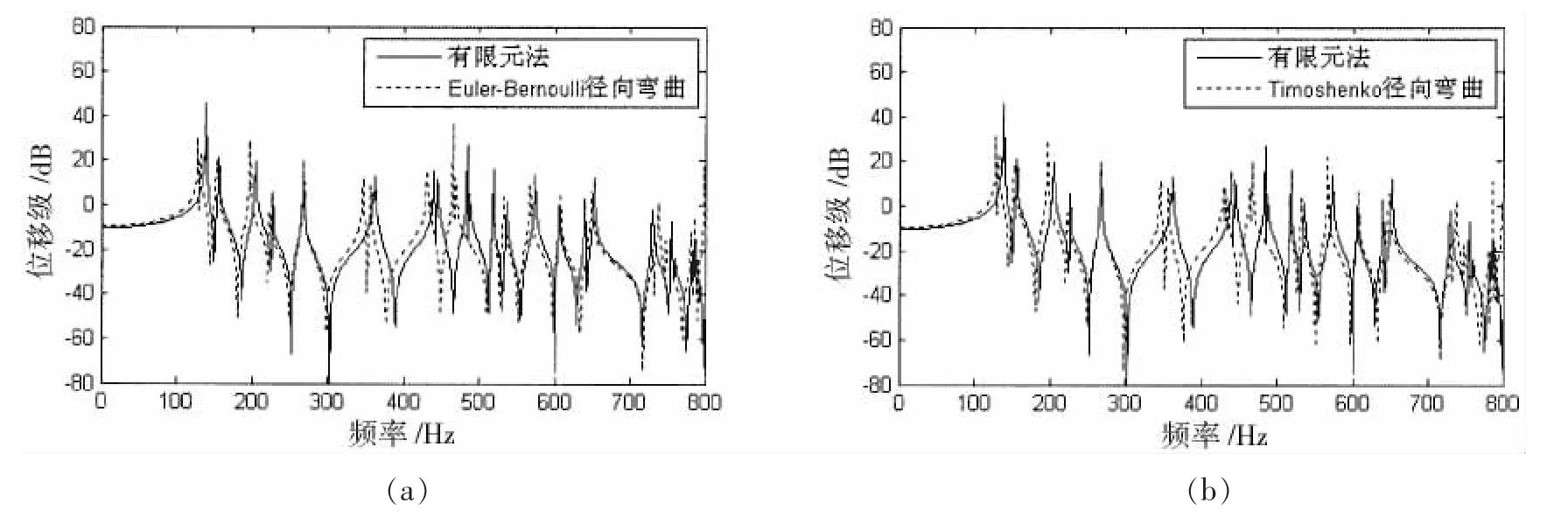
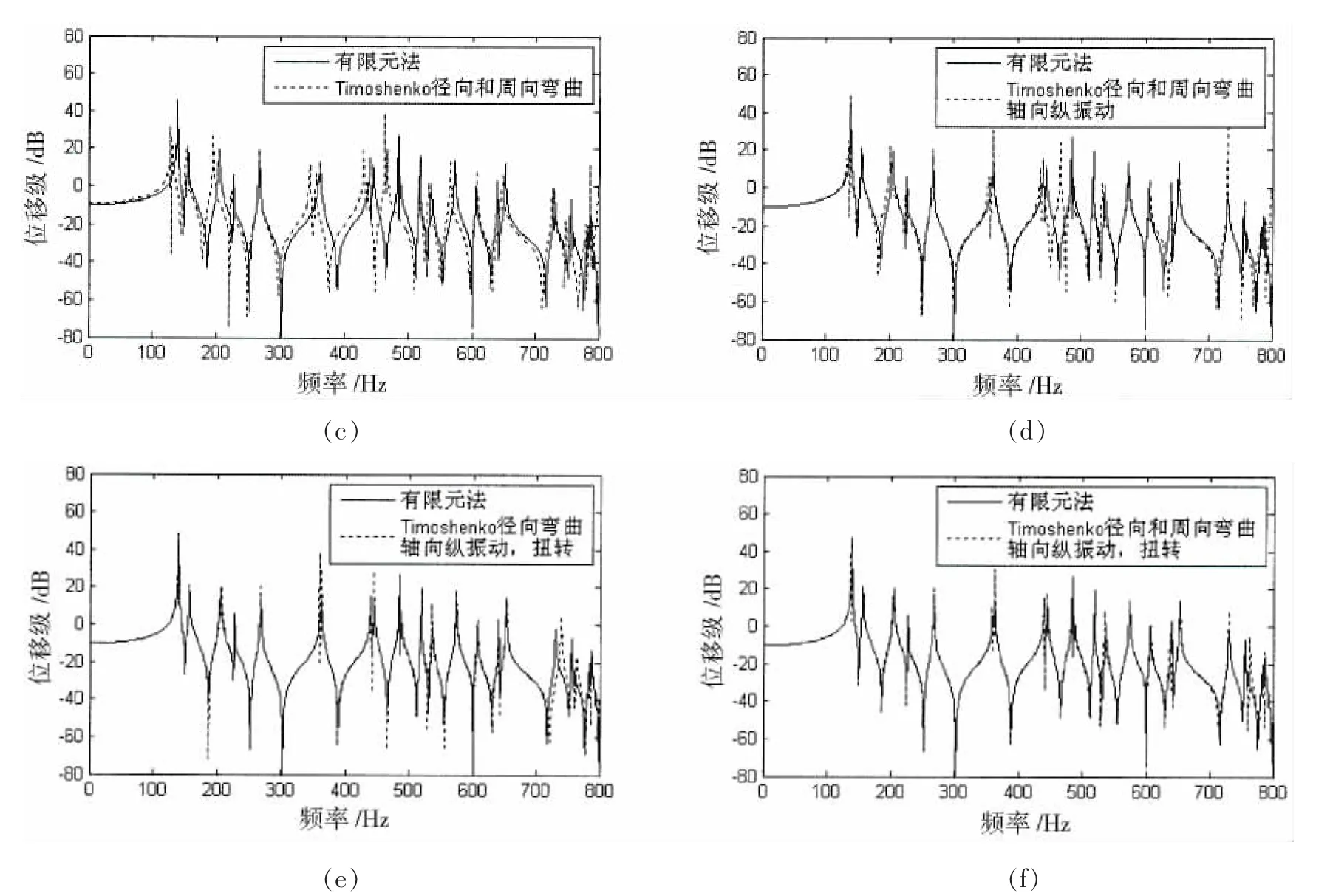
图2 不同纵肋建模方式圆柱壳振动响应与有限元结果比较Fig.2 Comparison of displacement responses of longitudinally stiffened cylindrical shell by different analytical methods and by finite element method

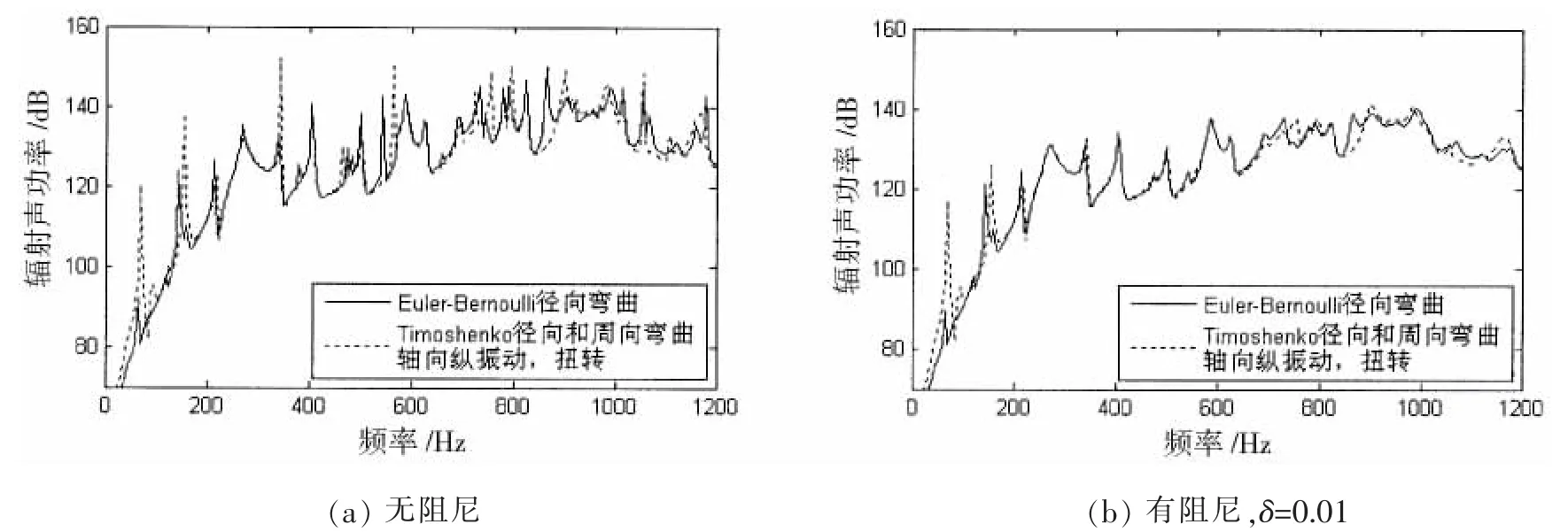
图3 不同纵肋建模方法圆柱壳辐射声功率比较Fig.3 Comparison of sound radiated power from cylindrical shell by different longitudinal stiffener modeling

3 振动及声辐射计算分析

在表1模型的基础上，壳体引入0.01的阻尼损耗因子，改变纵肋数目，在低频段，计算纵肋加强圆柱壳的辐射声功率和壳面均方振速，分析纵肋对圆柱壳振动声辐射的影响规律。纵肋建模方法基于Timoshenko梁理论，并同时考虑了纵肋对圆柱壳各个方向的作用力。

3.1 模态分析

图4给出了两条纵肋加强圆柱壳空气中的部分典型振动模态，并与无肋圆柱壳的振动模态进行了比较。大量的模态比较发现，在低频段，对于一个无肋圆柱壳模态，一般都能发现与之模态振形对应的加纵肋圆柱壳模态，如图 4 中（b）、（c）与（a），（e）、（f）与（d），但是由于纵肋在模态振形中所处位置不同，相应的模态频率也不同。当纵肋在波腹位置时，更多程度上起质量负载的作用，模态频率相应低一些，当纵肋在波节位置时，对壳体模态振动影响较小，模态频率与无肋壳接近。随着模态阶数的升高，纵肋的存在会导致原本的圆柱壳模态发生畸变，如图4（e）。总之，加入纵肋后，圆柱壳的低频振动模态数增多，模态频率也发生了不同程度的偏移，这将会在一定程度上影响到壳体振动响应和辐射声功率。

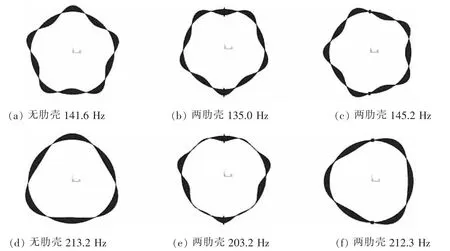
图4 纵肋对圆柱壳振动模态的影响Fig.4 Effect of longitudinal stiffener to vibration mode of cylindrical shell

3.2 振动分析

在空气中振动模态分析的基础上，进行了水下壳体振动分析，图5给出了不同纵肋数目下圆柱壳的壳体均方振速，在200 Hz以下的低频段，加入纵肋后，均方振速谐振峰发生了一定的频移，幅值也有不同程度的改变；在200 Hz以上的高频段，加入纵肋后，结合轴向振型变化分析，壳体均方振速明显降低，并且纵肋数目越多降低程度越大。总体上，纵肋对中高频圆柱壳均方振速抑制作用比较明显。

图5 纵肋对圆柱壳均方振速的影响Fig.5 Effect of longitudinal stiffener to mean radial quadratic velocity of cylindrical shell

为进一步分析纵肋加强圆柱壳的低频振动特性，对比分析了加肋前后圆柱壳表面位移分布，这里以90 Hz和215 Hz两个频率为例，恰为加入纵肋后出现新的辐射声功率峰的位置，更能反应出加纵肋前后圆柱壳振动与声辐射特性的差异，位移分布如图6所示，其中激励力在（φ=0，z=0），两条纵肋分别位于φ=0和φ=π。可以发现，加入纵肋后，圆柱壳表面位移分布呈现出更加明显的轴向条纹特性，与无肋壳相比，加肋壳的表面振动分布更加均匀，并且振动幅值也更大，这与高频段纵肋使圆柱壳均方振速降低的特性是相反的。图7进一步从圆柱壳表面声强分布的角度，对比分析了纵肋对圆柱壳声辐射能的影响，可以发现，低频段加肋后圆柱壳的表面声强分布形状改变不大，但是声强幅值明显增加。因此，当激励力作用在纵肋上时，纵肋带动壳体整体运动，在部分频率处，纵肋可使壳面振动增强，耦合声能也相应更加。

图6 圆柱壳表面位移分布Fig.6 Distribution of displacement on cylindrical shell surface

图7 圆柱壳表面声强分布Fig.7 Distribution of sound intensity on cylindrical shell surface

3.3 声辐射分析

首先从模态叠加的角度分析纵肋对圆柱壳声辐射的影响。由（5）式可知，辐射声功率可由多个辐射声功率模态线性叠加而成，称为（n，m）阶辐射声功率模态。图8给出了光壳时圆柱壳总的辐射声功率和前几阶辐射声功率模态，可以看出，在低频段，总辐射声功率主要由前几阶辐射声功率模态构成，且每个辐射声功率模态曲线比较平滑，仅有一个峰。图9给出了含2条纵肋加强圆柱壳的不同辐射声功率模态，可以看到每个辐射声功率模态有一个主峰的同时，还出现了很多个次峰，在更多纵肋数目加强圆柱壳的分析中也发现了类似的现象，这与光壳明显不同。还可以发现部分次峰数值较大，已成为构成总辐射声功率的重要部分。对于光壳而言，双三角函数描述的圆柱壳模态是正交的，加入纵肋后，圆柱壳周向不再均匀，仍采用双三角函数描述的圆柱壳模态将导致模态耦合，由（12）式可知，纵肋对圆柱壳的第m阶模态的作用力不仅与第m阶模态的位移有关，还与其它模态的位移有关，因此，加入纵肋后圆柱壳的周向模态发生了耦合，这就使得第m阶辐射声功率模态不再仅与第m阶振动模态有关，还与其它的振动模态有关，从而每个辐射声功率模态出现了很多个谐振峰。

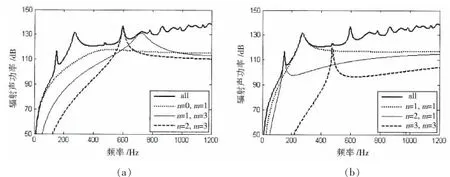
图8 光壳圆柱壳辐射声功率模态分析Fig.8 Modal analysis of sound radiated power of bare cylindrical shell

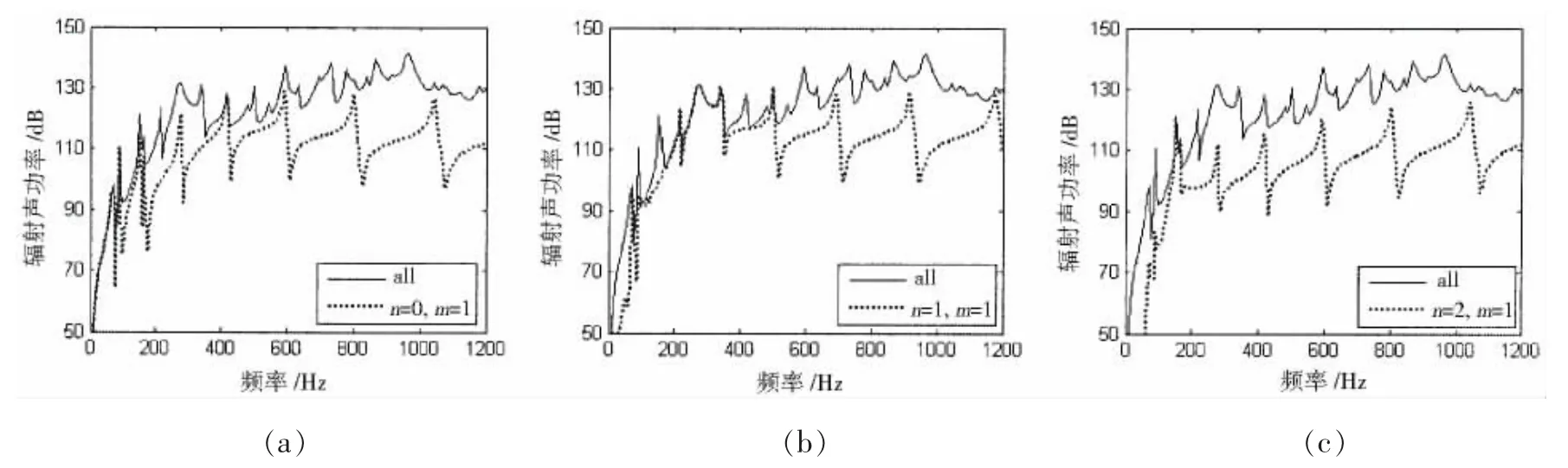
图9 含2条纵肋加强圆柱壳辐射声功率模态分析Fig.9 Modal analysis of sound radiated power of cylindrical shell with two longitudinal stiffeners

下面从声辐射效率的角度分析纵肋对圆柱壳声辐射的影响。图10给出了无肋壳与加肋壳声辐射效率的比较，可以看出，总体上加肋壳的声辐射效率要高于无肋壳，这是由于加肋后，肋带动壳体整体振动，使得壳体振动分布更加均匀，这在图6中可以得到印证，从而加肋后壳体的声辐射效率更高。但在高于1 000 Hz的频段上，加肋后声辐射效率有所降低，这是由于在高频段主要以高阶模态为主，波长相对较短，使得肋的作用没有低频明显，导致加肋壳的声辐射效率趋于无肋壳。

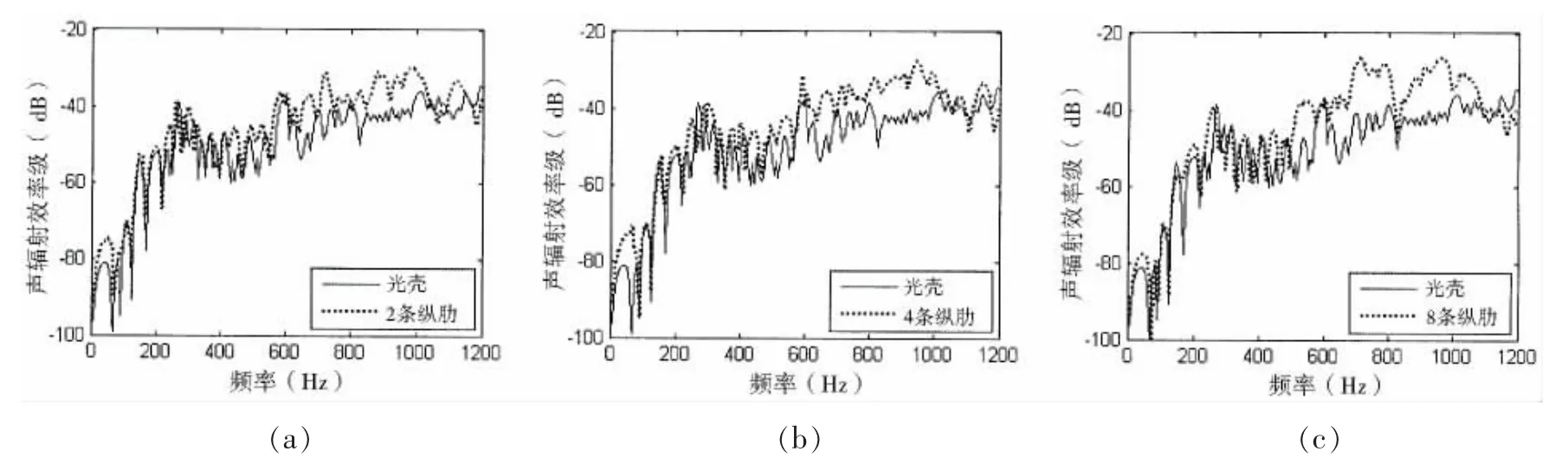
图10 纵肋对圆柱壳声辐射效率的影响Fig.10 Effect of longitudinal stiffener to sound radiation efficiency of cylindrical shell

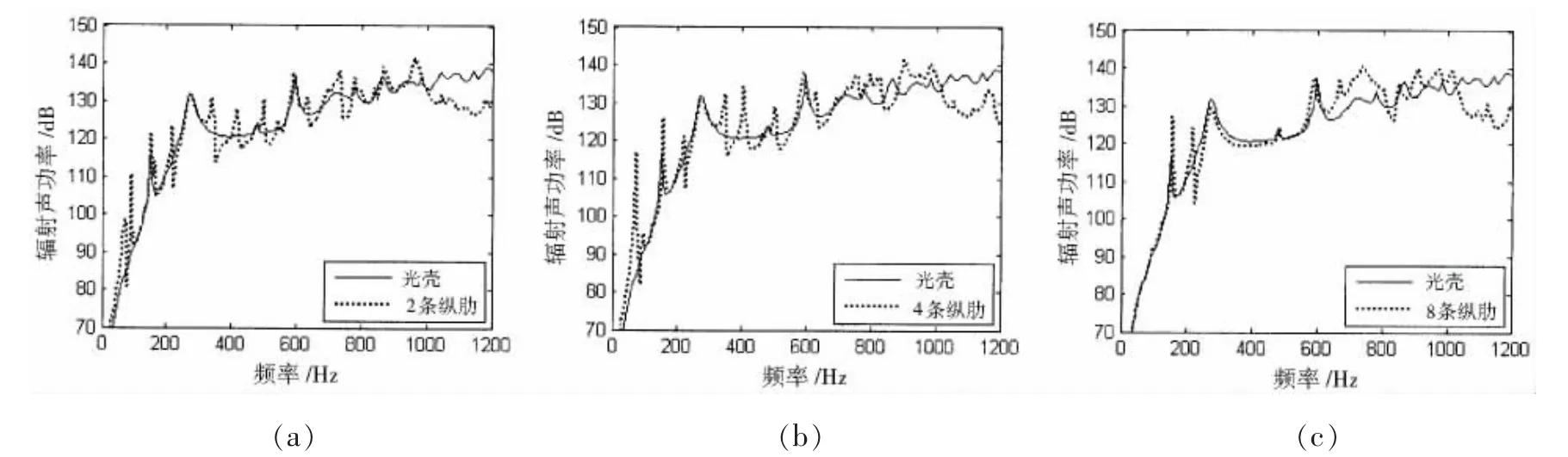
图11 纵肋对圆柱壳辐射声功率的影响Fig.11 Effect of longitudinal stiffener to sound radiated power of cylindrical shell

在模态分析、声辐射效率分析的基础上，进一步对总的辐射声功率进行分析，图11分别计算了2条、4条和8条纵肋加强圆柱壳的辐射声功率，并与无肋圆柱壳进行了对比。可以发现，在1 000 Hz以下的低频段，加入纵肋后圆柱壳辐射声功率产生了许多新的峰，通过前文分析可知，新峰是由于纵肋的引入使得圆柱壳周向产生了不均匀性，使得周向模态发生耦合，在多个频率处发生声辐射谐振导致的，另外从低频壳体振动分布来看，部分频率处加肋后壳面振动增强，也导致了部分频率处辐射声功率的增加。低频新辐射峰的出现，使得加肋圆柱壳的低频辐射声功率线谱更加丰富，这对降低圆柱壳低频声辐射是不利的，但随着纵肋数目的增加，圆柱壳周向不均匀性减小，辐射声功率峰也逐渐减少。在1 000 Hz以上的高频段，加纵肋后，由于声辐射效率趋于无肋壳，而壳面均方振速却明显低于无肋壳，所以导致加肋后辐射声功率明显降低，这对降低圆柱壳声辐射是有利的。

4 结 论

对传统的纵肋建模方法进行改进，建立了水下纵肋加强圆柱壳振动与声辐射解析计算模型，研究了低频段纵肋对圆柱壳振动声辐射的影响规律，得到如下结论：

（1）采用Euler-Bernoulli梁理论，仅考虑纵肋径向弯曲振动，能反应纵肋对圆柱壳作用的基本趋势，但会导致不同程度的谐振峰频偏误差，研究表明，纵肋的轴向纵振动和扭转振动也是重要的，本文采用Timoshenko梁理论，同时考虑纵肋各种作用力的建模与有限元数值解吻合较好；

（2）在低频段，纵肋使得圆柱壳振动模态更加丰富，壳面振动更加均匀，部分频率附近振动增强；在高频段，纵肋对圆柱壳均方振速具有明显的抑制作用；

（3）在低频段，纵肋使得圆柱壳周向模态互相耦合，辐射声功率形成许多新的峰，这对圆柱壳低频减振降噪是不利的；在更高频段上，加入纵肋后辐射声功率会明显降低，这对圆柱壳减振降噪是有利的。

[1]夏齐强,陈志坚,艾海峰.基于结构增抗技术的高腹板环肋双层圆柱壳声振设计研究[J].船舶力学,2013,17(5):522-529.Xia Qiqiang,Chen Zhijian,Ai Haifeng.Study on the vibro-acoustic design of high web plate for the ring-stiffened double cylindrical shell based on mechanical impedance improving[J].Journal of Ship Mechanics,2013,17(5):522-529.

[2]王路才,周其斗,纪 刚.加肋有限圆柱壳体的边界条件对其振动和声辐射的影响[J].船舶力学,2013,17(5):559-566.Wang Lucai,Zhou Qidou,Ji Gang.Effect on acoustic radiation of ribbed cylindrical shell due to boundary conditions[J].Journal of Ship Mechanics,2013,17(5):559-566.

[3]Ramachandran P,Narayanan S.Evaluation of modal density,radiation efficiency and acoustic response of longitudinally stiffened cylindrical shell[J].Journal of Sound and Vibration,2007,304(1-2):154-174.

[4]石焕文,盛美萍,孙进才,等.加纵肋平底圆柱壳振动和声辐射的FEM/BEM研究[J].振动与冲击,2006,25(2):88-92.Shi Huanwen,Sheng Meiping,Sun Jincai,et al.On FEM/BEM for the problems of vibration and acoustic radiation from an axially stiffented cylindrical shell with two end plates[J].Journal of Vibration and Shock,2006,25(2):88-92.

[5]陈军明,陈应波,黄玉盈.水中双向正交加肋圆柱壳体声辐射的有限元法[J].武汉理工大学学报,2004,26(4):74-76.Chen Junming,Chen Yingbo,Huang Yuying.Analysis of acoustic radiation from orthogonally stiffened cylindrical shell in water based on the finte element method[J].Journal of Wuhan University of Technology,2004,26(4):74-76.

[6]王路才,周其斗,纪 刚.纵桁对环肋圆柱壳水下振动与声辐射的影响[J].海军工程大学学报,2012,24(2):87-92.Wang Lucai,Zhou Qidou,Ji Gang.Effect of longitudinal beams on acoustic radiation of cylindrical shell[J].Journal of Naval University of Engineering,2012,24(2):87-92.

[7]曾革委,黄玉盈,谢官模.外壳板采用纵骨加强的双层加肋圆柱壳水下声辐射分析[J].中国造船,2003,44(2):45-52.Zeng Gewei,Huang Yuying,Xie Guanmo.Acoustic radiation from fluid-loaded infinite circular cylindrical double-shell reinforced by transverse and axial stiffeners[J].Shipbuilding of China,2003,44(2):45-52.

[8]谢官模,李军向,罗 斌,等.环肋舱壁和纵骨加强的无限长圆柱壳在水下的声辐射特性[J].船舶力学,2004,8(2):101-108.Xie Guanmo,Li Junxiang,Luo Bin,et al.Sound radiation from fluid-loaded infinite cylindrical shells with rings,bulkhead and longitudinal stiffeners[J].Journal of Ship Mechanics,2004,8(2):101-108.

[9]廖长江,蒋伟康,王 云,等.水中有限长纵向加肋圆柱壳体振动与声辐射影响因素研究[J].振动与冲击,2009,28(5):74-83.Liao Changjiang,Jiang Weikang,Wang Yun,et al.Vibration and acoustic radiation of axially stiffened finite cylindrical shells in water[J].Journal of Vibration and Shock,2009,28(5):74-83.

[10]陈美霞,骆东平,王祖华,等.激励力对双层圆柱壳声辐射性能的影响[J].船舶力学,2005,9(2):124-130.Chen Meixia,Luo Dongping,Wang Zuhua,et al.Effect of driving forces property on characteristics of sound radiation from finite double cylindrical shell[J].Journal of Ship Mechanics,2005,9(2):124-130.

[11]陶 猛,范 军,汤渭霖.覆盖多柔性层的有限长圆柱壳声辐射特性[J].声学学报,2008,33(3):220-225.Tao Meng,Fan Jun,Tang Weilin.The characteristics of sound radiation from a cylindrical shell coated with multiple compliant layers[J].Acta Acustica,2008,33(3):220-225.

[12]宋郁民,吴定俊,李 奇.圆弧曲梁振动微分方程推导及振动特性分析[J].沈阳建筑大学学报,2012,28(3):400-404.Song Yumin,Wu Dingjun,Li Qi.Derivation of vibration differential equation and analysis of vibration properties about ARC-curved beam[J].Journal of Shenyang Jianzhu University(Natural Science),2012,28(3):400-404.

[13]张英世.变截面开口薄壁杆约束扭转振动的主振型函数之正交性[J].振动与冲击,1998,17(3):80-81.Zhang Yingshi.Orthogonality of vibration mode function for restrained torsional vibration of open thin-valled bars with variable cross sections[J].Journal of Vibration and Shock,1998,17(3):80-81.