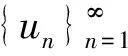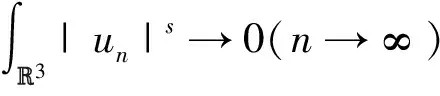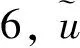一类Kirchhoff型方程基态解的存在性

杨玉蓓

(武汉工程大学邮电与信息工程学院 机械与电气工程系， 湖北 武汉 430074)

0 引 言

Kirchhoff型方程

(1)

引起了学者的广泛关注， 其中Ω是RN上的一个光滑区域,a,b是正常数， 非线性项f∈C(Ω×R，R), 方程(1)与Kirchhoff在文献[1]中提出的稳态方程

(2)

具有紧密联系. 方程(2)是一类经典的自由振动的弹性弦D’Alembert方程. Kirchhoff模型考虑了横向振动所导致的弦长度的变化. 在式(2)中,u代表位移，f(x,u)代表外力作用，b代表初始张力，a与弦的固有性质有关(比如弹性模量)， 同时式(2)在生物系统中也有较为广泛地应用， 其中u可以表示一个生物进程的平均状态(如人口密度).

的全体特征值.

在文献[5]中, He Xiaoming和Zou Wenming将方程(1)中的f(x,u)替换为λf(x,u), 其中λf(x,s)满足:

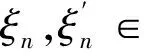
文献[5]运用局部极小方法和喷泉定理证明了对于任意的λ>0, 方程(1)具有无穷多解.

Chen Chingyu, Kuo Yuehching和Wu Tsungfang在文献[6]中考虑了如式(3)的Kirchhoff型方程

(3)

x∈R3,u∈H1(R3)(4)

已经被许多学者广泛地研究, 其中f∈C(R3×R,R),a,b>0， 是常数.

He Xiaoming和Zou Wenming在文献[7]中研究了方程(4)， 其中f(x,u)∶=f(u)∈C1(R+,R+)满足Ambrosetti-Rabinowitz条件 ((AR)条件)即

类似地， 文献[8-10]运用与文献[7]相类似的方法证明了当f(x,u)呈临界增长， 即f(x,u)形如λ|u|p-2u+|u|4u(4

对于非线性项f(x,u)=|u|p-2u(3

1 主要结果及其证明

我们研究Kirchhoff型方程

(5)

我们的主要结果如下.

在证明主定理之前， 先证明几个引理.

方程(5)所对应的能量泛函为

根据文献[12], 如果u∈H1(R3)是方程(5)的解, 则有Pohozaev恒等式

引入流形

M∶={u∈H1(R3){0}∶G(u)=0},

其中

故G(u)=〈I′(u),u〉+zP(u)， 其中P(u)在式(6) 中已给出.

显然， 若u∈H1(R3)是方程(1)的非平凡弱解, 则根据式(6), (7), 必有u∈M.

证明对于任意的u∈H1(R3){0}以及t>0, 取ut(x)∶=tu(t-2x). 考虑

γ(t)∶=Im(ut)=

引理2I具有山路定理的几何结构.

证明∃ρ,δ>0足够小使得

(‖u‖H1(R3)=p>0).

固定u∈H1(R3){0}, 取ut(x)∶=tu(t-2x), 对于足够大的t>0， 有

则∃t0>0, 取u0∶=ut0,I(u0)<0.

因此， 我们可以定义泛函I的山路值

(8)

其中

Γ∶={γ∈C([0,1],H1(R3))∶γ(0)=0,

I(γ(1))<0}.(9)

引理3 (一般极小极大原理， 参见文献[13]定理2.8) 设X是Banach空间. 令M0是度量空间M的闭子空间并且Γ0⊂C(M0,X). 定义

Γ∶={γ∈C(M,X)∶γ|M0∈Γ0}.

如果φ∈C1(X,R)满足

(a)c-2ε≤φ(u)≤c+2ε,

(b) dist(u,γ(M))≤2δ,

(c) ‖φ′(u)‖≤8ε/δ.

I(un)→c,I′(un)→0,G(un)→0.(10)

证明定义映射Φ∶R×H1(R3)→H1(R3),Φ(θ,v)=eθv(e-2θx), 其中θ∈R,v∈H1(R3)并且x∈R3. 对于任意的θ∈R,v∈H1(R3), 考虑泛函

根据引理3, 容易验证对于全体满足|θ|, ‖v‖H1(R3)足够小的(θ,v), 存在I∘Φ(θ,v)>0, 并且(I∘Φ)(0,u0)<0, 即I∘Φ在R×H1(R3)上满足山路定理的几何结构. 我们可以定义泛函I∘Φ的山路值

(11)

其中

(Ι∘Φ)(θn,vn)→c,(13)

(I·Φ)′(θn,vn)→0于(R×H1(R3))-1,(14)

θn→0.(15)

对每个(h,w)∈R×H1(R3),

〈(I∘Φ)′(θn,vn),(h,w)〉=

〈I′(Φ(θn,vn)),Φ(θn,w)〉+G(Φ(θn,vn))h.(16)

在式(16)中取h=1,w=0, 我们有G(Φ(θn,vn))→0(n→∞). 记un∶=Φ(θn,vn), 我们有G(un)→0(n→∞).

另外, 运用类似于文献[14,15]的方法, 我们可以证明

(17)

证明根据式(10)， 可得

从而我们得到了‖un‖H1(R3)的上界.

引理6 存在序列{xn}⊂R3以及R>0,β>0使得

其中{un}在式(10)中已提及.

故un→0于H1(RN). 又由于I(un)→c, 则与c>0相矛盾.

(19)

(20)

[1] Kirchhoff G. Mechanik[M]. Teubner: Leipzig, 1883.

[2] Lions J L. On some questions in boundary value problems of mathematical physics[J]. North-Holland Math. Studies, 1978: 30(1): 284-346.

[3] Ding Weiyue, Ni Weiming. On the existence of positive entire solutions of a semilinear elliptic equation[J]. Archive for Rational Mechanics and Analysis, 1986, 91(4)： 283-308.

[4] Perera K, Zhang Zhitao. Nontrivial solutions of Kirchhoff-type problems via the Yang index[J]. Journal of Differential Equations, 2006, 221(1)： 246-255.

[5] He Xiaoming, Zou Wenming, Infinitely many positive solutions for Kirchhoff-type problems[J]. Nonlinear Analysis, 2009, 70(3)： 1407-1414.

[6] Chen Chingyu, Kuo Yuehcheng, Wu Tsungfang. The Nehari manifold for a Kirchhoff type problem involving sign-changing weight functions[J]. Journal of Differential Equations， 2011, 250(4)： 1876-1908.

[7] He Xiaoming, Zou Wenming. Existence and concentration behavior of positive solutions for a kirchhoff equation in[J]. Journal Differential Equations, 2012, 252(2)： 1813-1834.

[8] Wang Jun, Tian Lixin, Xu Junxiang, et al. Multiplicity and concentration of positive solutions for a Kirchhoff type problem with critical growth[J]. Journal of Differential Equations 2012, 253(7)： 2314-2351.

[9] He Yi, Li Gongbao, Peng Shuangjie. Concentrating bound states for Kirchhoff type problems in involving critical Sobolev exponents[J]. Advanced Nonlinear Studies, 2014, 14(2)： 441-468.

[10] Li Gongbao, Ye Hongyu. Existence of positive solutions for nonlinear Kirchhoff type equations in with critical Sobolev exponent[J]. Mathematical Methods in the Applied Science， 2014, 37(16)： 2570-2584.

[11] Li Gongbao, Ye Hongyu. Existence of positive ground state solutions for the nonlinear Kirchhoff type equations in[J]. Journal Differential Equations, 2014, 257(2)： 566-600.

[12] Pucci P, Serrin J, A general variational identity[J]. Indiana University Mathematics Journal， 1986, 35(3)： 681-703.

[13] Willem M. Minimax Theorems[M]. Boston: Birkhäuser Boston, 1996.

[14] Arosio A, Panizzi S. On the well-posedness of the Kirchhoff string[J]. Transactions of the American Mathematical Society, 1996, 348(1)： 305-330.

[15] Rabinowitz P. On a class of nonlinear Schrödinger equations[J]. Zeitschrift Für Angewandte Mathematik and Physik， 1992, 43(2)： 270-291.