紧框架小波和总广义全变分联合约束的医学图像复原算法

张 晶， 马 瑾， 邵 晨， 桂志国， 张 权， 杨 婕,

(1. 山西财贸职业技术学院 信息工程系， 山西 太原 030031； 2. 山西中医药大学 医药管理学院， 山西 太原 030619； 3. 中北大学 信息与通讯工程学院， 山西 太原 030051)

0 引 言

在图像的成像、 采集和传输过程中， 成像设备或其他物理因素会不可避免地造成图像质量退化， 为使图像质量满足实际应用(如医疗、 军事、 交通等)要求， 研究图像降噪、 图像去模糊化、 图像修复以及图像重建等图像复原技术[1-2]非常有必要. 通常情况下， 图像复原可以看作一个典型的通过对退化图像的近似数学估计模型进行求逆的不适定问题

f=Aλ+η,(1)

式中：f表示观测到的退化图像；A是一个病态的线性算子；η为加性随机噪声. 由于设备和噪声等因素的限制， 很难构建模拟图像退化的准确数学模型； 即使能够建立准确的估计模型， 数据的大规模性及算法模型的非光滑性也会致使有效的优化估计方法很难获得. 因此， 图像复原技术所需解决的两个关键问题为图像质量退化模型的建立和相应优化估计算法的设计[3].

对于退化模型的构建， 国内外学者的研究焦点集中在由保真项和正则项构成的能量泛函约束的正则化复原模型上. 就保真项而言， 由高斯、 泊松噪声所致的图像退化常由光滑的泛函L2范数来拟合； 由椒盐噪声引发的图像退化则由非光滑的泛函L1范数来拟合[3，4]. 就正则项而言， 通过利用如全变分、 小波、 剪切波、 紧框架小波等变换的稀疏性， 图像的先验信息可以被很好地表征[5]. 对于退化模型的求解， 主要有直接方法和分解方法. 直接方法同时处理保真项和拟合项， 如果该两项均为光滑泛函， 可通过梯度下降法和牛顿迭代法求解； 如果仅保真项是光滑的， 则当正则项为有界全变分时可将模型转换为变分偏微分方程， 进而进行数值求解； 此外， 根据保真项和拟合项的特性， 还可通过Fenchel变换将模型转换为对偶问题求解等[4,6，7]. 从式(1)所示的线性不适定的逆问题中恢复高质量图像的关键是选取能够合理表征图像先验的正则项， 近年比较成功的正则项约束的复原方法有Rudin-Osher-Fatemi模型[8]、 非局部变型[9，10]、 inf-卷积模型[11]、 TGV模型[12]、 联合一阶、 二阶全变分模型[13]以及Gabor框架、 小波框架、 剪切波等多尺度应用谐波分析方法[1,14，15]. 一般地， 基于泛函Lp(p=0,1,2)的范数正则项约束的复原模型等价于求解最小化问题

(2)

式中：Φ表示某种具有稀疏性的线性变换.

为了解决由全变分函数的“分片常数”效应导致的阶梯状伪边缘、 由稀疏逼近算法的精确性导致的尖锐边缘及细节信息丢失等问题， 本文通过构造能够完备表征图像特性的稀疏正则项及设计目标函数迭代优化估计方法来提高复原图像的质量. 仅采用一种小波基函数很难准确描述图像特征， 通过构造能够利用小波框架函数族对图像进行稀疏表示的紧框架小波来提高图像描述的准确性； 此外， TGV函数具有凸性、 旋转不变性以及下半函数连续性， 通过逼近由多项式组成的任意阶函数， 可以从原理上克服TV方法的“分片常数”效应， 进而解决阶梯状伪边缘问题. 由此， 本文构造了一种由紧框架小波和二阶TGV组成的稀疏正则项， 并以所构造的正则项为约束进行图像复原. 由于新的复原模型由光滑L2范数和非光滑L1范数泛函共同组成， 故直接求解难度较高. 本文首先通过辅助变量将具有混合泛函的目标函数最小化问题分解为两个子问题， 进而分别采用均值增广拉格朗日算法和Chambolle-Pock原始—对偶迭代方法获得最优解.

1 基本理论

1.1 紧框架小波

对于任意一个可数集χ⊆L2(Rd,d∈N)，L2(Rd) 上的紧框架[16-17]定义为

Rd),(3)

式中： 〈·,·〉表示L2(Rd)上的内积， 且〈f,φ〉称为f的典型系数. 若给定Ψ={ψl∶l=1,…,r}⊆L2(Rd)， 则

χN∈N(Ψ)={ψl,n,k∶1≤l≤r,n∈Z,k∈Zd},(4)

则L2(Rd)上的紧框架小波χN(Ψ)的每一个紧框架ψ1,…,ψr函数由对称紧支撑函数组成， 若

则基于多分辨率分析的紧框架Ψ构造可通过寻找有限支撑的ql使其满足

[k]φ(2x-k),

l=1,…,r.(7)

基于酉扩张原理(Unitary Extension Principle， UEP)可得

Rd,(8)

例如，L2(Rd)上的分段线性B样条(B-spline)函数为

(10)

二维离散快速紧框架变换的定义为

Wλ={Wl,αλ∶(l,α)∈Γ},(11)

式中： Γ=({0,…,L-1}×B)∪{(L-1,0)}， 紧支撑子带B={0,…,r}2{0}， 则λ∈I2在第l层α子带的紧支撑系数为

Wl,αλ=ql,α[-·](*)λ,(12)

此处， (*)表示具有一定边界条件的离散卷积， 且

(13)

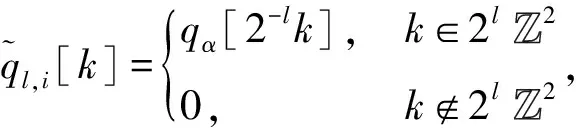
λ=WTWλ.(14)

1.2 总广义全变分

近年来， 被广泛采用的基于全变差(Total Variation， TV)正则项约束的复原模型虽然能够保持图像的尖锐边缘， 但会产生块状或阶梯状伪边缘. 针对这一不足， 一种广义TV即TGV法被引入到图像复原处理中. 与仅考虑一阶导数的TV不同， TGV能够考虑高阶导数， 对于分段多项式函数或尖锐边缘处理效果较好.k阶TGV定义[18]为

‖divlφ‖∞≤αl},(15)

(17)

(18)

广义变分有界空间定义为

(19)

2 算法模型及优化估计

2.1 算法简介

通过构造能够完备表征图像特性的稀疏正则项， 本文提出了一种紧框架小波和总广义全变分联合约束的图像复原算法. 算法模型为

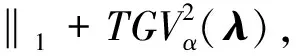
s.t. ϑ=Wλ,(21)

式中： 第一项为保真项， 确保复原图像尽可能保留原图像的重要特征； 第二项和第三项为联合正则项. 本文方法的设计主要是为了合理发挥紧框架小波和二阶TGV表征待复原图像先验信息的优越性. 一方面， 二阶TGV能够在平滑噪声的同时克服“阶梯伪影效应”； 另一方面， 紧框架小波变换具有稀疏性， 能够抑制重要纹理细节信息的丢失. 如式(21)所示， 本文方法所需解决的问题为条件约束的最小化问题， 采用双重增广拉格朗日算法[19](Doubly augmented Lagrangian， DAL)将该有约束的最小化问题变为无约束的问题， 即

(22)

其中，

(23)

由于该含光滑L2范数和非光滑L1范数泛函的最小化复原模型求解难度较高. 本文通过引入辅助变量μ来简化求解过程， 即式(23)等价于

(24)

进而可将式(24)分解为两个子问题， 即

(25)

对于子问题(1)， 通过进一步计算可得

(26)

进而有

(27)

ϑj+1=Hβ1,κ,γ(Wλj+1+υj,ϑj),(28)

υj+1=υj+Wλj+1-ϑj+1.(29)

通过广义硬阈值收缩求解式(28)， 得

(30)

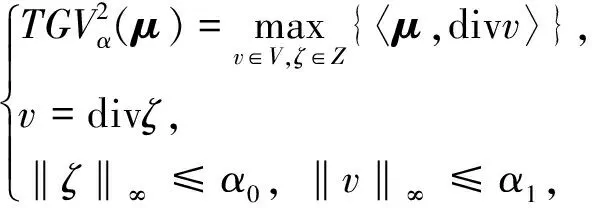
令

采用一阶原始对偶算法可以得出

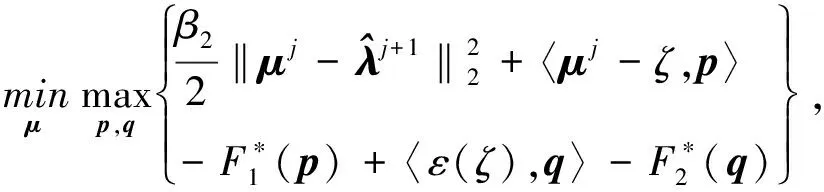
其中

(33)

进一步进行迭代求解

(34)

其中，

2.2 算法流程

算法任务：

紧框架小波和总广义全变分联合约束的图像复原算法.

参数初始化

While 不满足停步准则

第一步 求解子问题(1)， 给定μj，

1. 更新λj+1， 采用公式(27)；

2. 更新ϑj+1， 采用公式(28)；

3. 更新υj+1， 采用公式(29)；

第二步 求解子问题(2)， 采用求出的λj+1，

5. 更新μj+1， 采用公式(34)；

j=j+1

结束

输出质量改善的复原图像

3 实验与分析

本文实验对象为以 “lena”和“brain_tumor”命名的标准图像(如图 1 所示)， 对噪声水平为σ=6时的退化图像(如图 2 所示)进行复原实验.

图 1 本文实验采用的标准图像Fig.1 The standard images used in the experiments

图 2 σ=6时的质量退化图像Fig.2 When σ=6, the degraded images used in the experiments

实验中计算机硬件配置为： Intel(R) Core(TM) i5-6500 CPU @ 3.20 GHz， Windows7 32位操作系统； 软件环境为： MATLAB R2014a. 复原图像质量量化评价指标为峰值信噪比(Peak Signal to Noise Ratio， PSNR)和结构相似度(Structural Similarity Index， SSIM)， 定义为

(36)

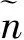
其中， 式(39)目标函数的正则项为TV， 式(40)目标函数的正则项为二阶TGV. 本文算法迭代停步条件为

4.5×10-4.

图 3 给出了分别采用TV、 TGV以及本文方法对退化lena进行复原的实验结果. 可以发现， TV的“分片常数”导致图3(b)中有大量块状和阶梯状的伪边缘出现； 图3(c)很好地说明了二阶TGV在抑制噪声和阶梯伪影方面的优势； 从图3(d) 可以看出本文方法在细节和纹理信息方面复原情况更好. 图4为图3中各实验结果图中局部放大图像， 直观地， 如图中箭头所示， 本文方法可以很好地改善TV结果图1中块状和阶梯状伪边缘情况， 同时在细节和纹理结构的复原方面又优越于TGV方法.

图 3 采用不同算法复原后的lena图像Fig.3 The restored lena images obtained by different methods

为了进一步说明本文所提方法的有效性， 对各复原图的不同感兴趣区(Region of Interest， ROI)进行标化， 如图 5 所示， 并对其量化指标表现情况进行比较， 如表 1 所示. 结果标明： 在ROI1和ROI2内， 本文方法结果图的PSNR值最大， 表明通过本文方法所获复原图失真较小， 与原始的标准图像更加接近； 类似地， 本文方法结果图的SSIM值也最大， 说明本文方法复原图与原始标准图像的结构更加相似.

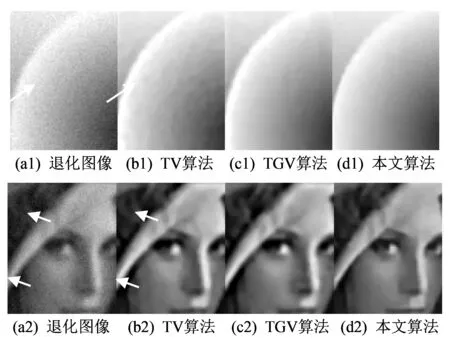
图 4 采用不同算法复原后的lena局部图像Fig.4 The partial images of the restored lena images in Fig.3

图 5 不同感兴趣区的lena和brain_tumor 图Fig.5 The lena and brain_tumor images with region of interest (ROI) marked

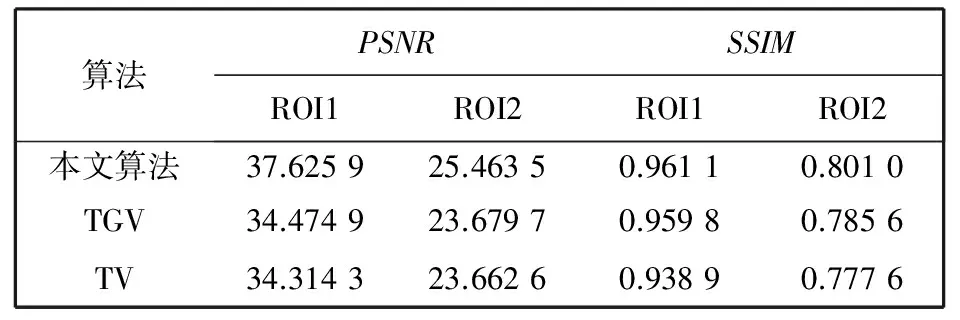
算法PSNRSSIMROI1ROI2ROI1ROI2本文算法37．625925．46350．96110．8010TGV34．474923．67970．95980．7856TV34．314323．66260．93890．7776

图 6 为分别采用TV、 TGV以及本文方法获取的brain_tumor图像复原图， 图7为图6中各个结果图像的局部放大图. 表 2 给出了基于brain_tumor复原图采用不同方法的量化指标表示情况. 一方面， 观察图6和图7可以发现， 与其他两种方法相比较， 本文方法所获结果图像的细节和纹理信息复原情况明显更好. 另一方面， 分析表2可以看出， 对于brain_tumor图像， 在ROI3和ROI4内， 本文方法结果图的PSNR值和SSIM值也是最大的， 说明本文方法复原图失真较小， 与原始标准图像的结构更加相似. 综上， 无论从直观视觉角度还是从客观量化分析角度， 本文方法较传统方法都表现出一定的优越性， 是可行和有效的.

图 6 采用不同算法复原后的brain_tumor图像Fig.6 The restored brain_tumor images obtained by different methods

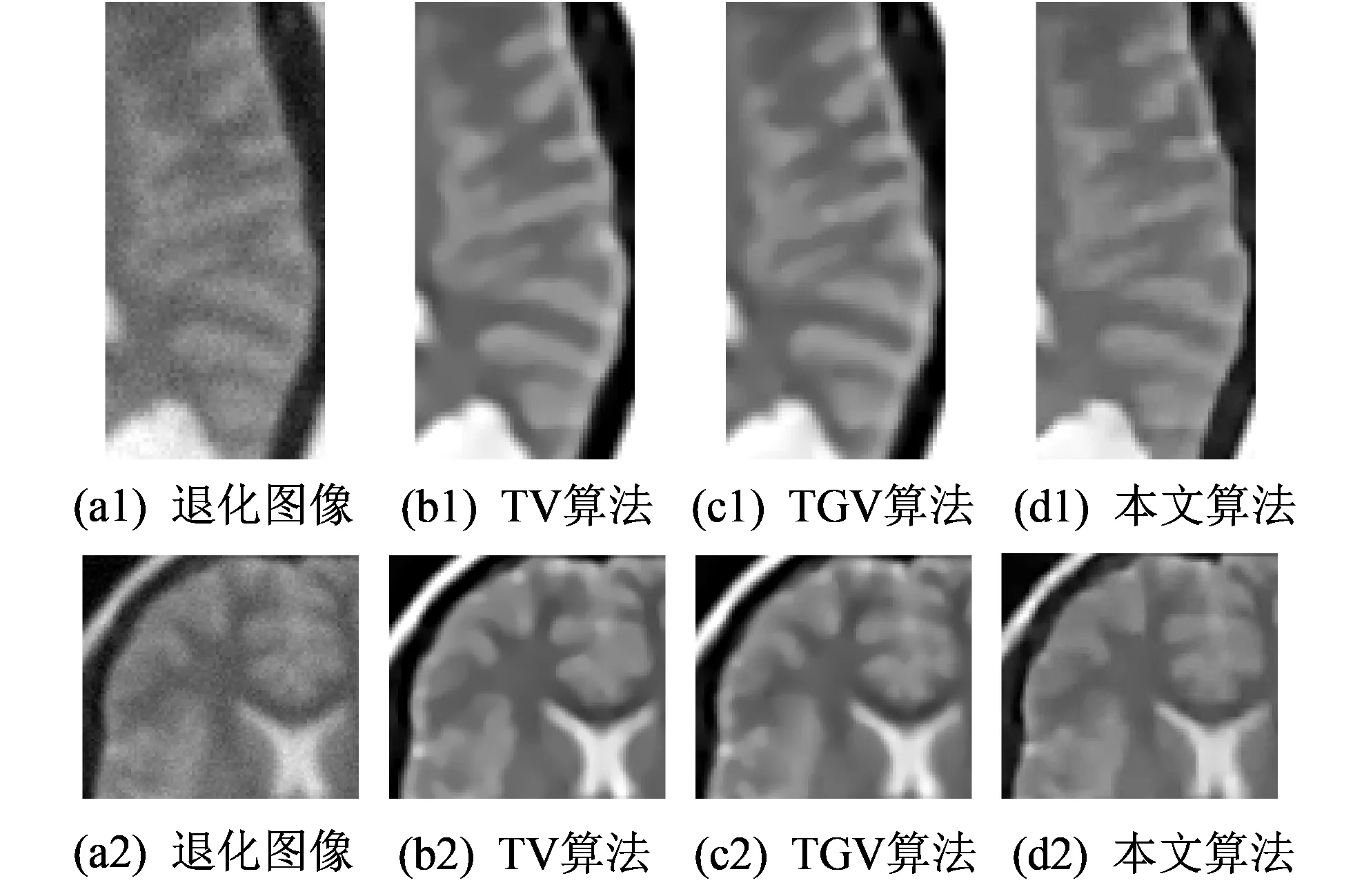
图 7 采用不同算法复原后的brain_tumor局部图像Fig.7 The partial images of the restored brain_tumor images in Fig.6

算法PSNRSSIMROI1ROI2ROI1ROI2本文算法27．573028．50380．82310．8378TGV24．655525．34440．80480．8157TV24．161424．34370．80290．8097

4 结束语

本文提出一种紧框架小波和总广义全变分联合约束的图像复原算法. 首先， 构造出一种由紧框架小波L1范数和二阶TGVL2范数组成的联合正则项约束的图像复原模型； 其次， 采用交替方向迭代方法将所建模型的最小化问题分解为两个子问题， 并分别采用均值增广拉格朗日算法和Chambolle-Pock一阶原始—对偶迭代方法获得最优解； 通过与其他复原算法进行仿真实验分析， 不管从视觉效果还是从量化指标分析来看， 本文方法不仅可以有效地抑制噪声， 而且在去模糊化后能够很好地保留纹理和细节信息， 使得复原后的结果图更接近原始图像. 因此， 该算法的提出有助于图像复原技术进一步的发展.

[1] Dong B, Jiang Q, Shen Z. Image restoration: wavelet frame shrinkage, nonlinear evolution PDEs, and beyond[J]. Multiscale Modeling & Simulation, 2017, 15(1)： 606-660.

[2] Katsaggelos A K. Digital image restoration[M]. New York: Springer Publishing Company, 2012.

[3] 李旭超, 马松岩, 边素轩. 对偶算法在紧框架域TV-L1去模糊模型中的应用[J]. 中国图象图形学报, 2015, 20(11)： 1434-1445.

Li Xuchao, Ma Sunyan, Bian Suxuan. Application of dual algorithm to TV-L1 deblurring model of frame domain[J]. Journal of Image and Graphics, 2015, 20(11)： 1434-1445. (in Chinese)

[4] 李旭超, 边素轩, 李玉叶, 等. 图像恢复中的凸能量泛函正则化模型综述[J]. 中国图象图形学报, 2016, 21(4)： 405-415.

Li Xuchao, Bian Suxuan, Li Yuye. Survey on convex energy functional regularization model of image restoration[J]. Journal of Image and Graphics, 2016, 21(4)： 405-415. (in Chinese)

[5] 陈芳芳. 基于变分原理的图像去噪研究[D]. 成都： 电子科技大学, 2016.

[6] Bertsekas D P, Scientific A. Convex optimization algorithms[M]. Belmont： Athena Scientific, 2015.

[7] 李旭超, 宋博. 原始-对偶模型的牛顿迭代原理与图像恢复[J]. 电子学报, 2015, 43(10)： 1984-1993.

Li Xuchao, Song Bo. Newton iterative principle of primal-dual model and image resroration[J]. Acta Electronica Sinica, 2015, 43(10)： 1984-1993. (in Chinese)

[8] 汪美玲, 周先春, 周林锋, 等. 全变分耦合图像去噪模型[J]. 通信学报, 2016, 37(4)： 182-191.

Wang Meiling, Zhou Xianchun, Zhou Linfeng. Coupling image denoising model based on total variation[J]. Journal on Communications, 2016, 37(4)： 182-191. (in Chinese)

[9] 张峥嵘, 黄丽丽, 费选, 等. 非局部TV正则化的图像泊松去噪模型与算法[J]. 系统仿真学报, 2014, 26(9)： 2110-2115.

Zhang Zhengrong, Huang Lili, Fei Xuan. Image poisson denoising model and algorithm based on nonlocal TV regularization[J]. Journal of System Simulation, 2014, 26(9)： 2110-2115.

[10] Liu J, Zheng X. A block nonlocal TV method for image restoration[J]. UCLA CAM report, 2016： 16-25.

[11] Bergounioux M. Mathematical analysis of a inf-convolution model for image processing[J]. Journal of Optimization Theory and Applications, 2016, 168(1)： 1-21.

[12] Bredies K, Holler M. Regularization of linear inverse problems with total generalized variation[J]. Journal of Inverse and Ill-posed Problems, 2014, 22(6)： 871-913.

[13] Papafitsoros K, Schönlieb C B. A combined first and second order variational approach for image reconstruction[J]. Journal of mathematical imaging and vision, 2014, 48(2)： 308-338.

[14] Cai J F, Dong B, Shen Z. Image restoration： a wavelet frame based model for piecewise smooth functions and beyond[J]. Applied and Computational Harmonic Analysis, 2016, 41(1)： 94-138.

[15] 吴玉莲, 冯象初. 利用平衡方法的非凸图像修复[J]. 西安电子科技大学学报, 2014, 41(5)： 141-147.

Wu Yulian, Feng Xiangchu. Nonconvex image inpainting via balanced regularization approach [J]. Journal of Xidian University, 2014, 41(5)： 141-147. (in Chinese)

[16] Daubechies I, Han B, Ron A, et al. Framelets： MRA-based constructions of wavelet frames[J]. Applied and Computational Harmonic Analysis, 2003, 14(1)： 1-46.

[17] Skopina M A. Tight wavelet frames[C]∥Doklady Mathematics. MAIK Nauka/Interperiodica, 2008, 77(2)： 182-185.

[18] Bredies K, Kunisch K, Pock T. Total generalized variation[J]. SIAM Journal on Imaging Sciences, 2010, 3(3)： 492-526.

[19] Dong B, Zhang Y. An efficient algorithm for l0minimization in wavelet frame based image restoration[J]. Journal of Scientific Computing, 2013, 54(2-3)： 350-368.