具有种群扩散的包虫病传播模型的研究

刘俊利， 刘璐菊， 冯进钤

(1. 西安工程大学 理学院， 陕西 西安 710048； 2. 河南科技大学 数学与统计学院, 河南 洛阳 471023)

0 引 言

包虫病也叫棘球蚴病， 是一种人兽共患寄生虫病， 如狗、 猪、 牛等家禽都可能被感染， 严重危害着人民的身体健康和生命安全， 是影响社会经济发展的重大传染病之一. 我国包虫病发病率最高的地区主要集中在西北部的牧业、 半农牧地区， 包括新疆、 甘肃、 宁夏、 内蒙古、 青海、 西藏、 四川[1-4]. 每年包虫病手术率超过1%， 高危人群高达5 000万人， 受包虫病威胁的家畜数量上亿， 其中犬类至少达500万只， 而羊的感染率高于50%[5,6]. 包虫病在世界很多国家都存在， 如意大利、 澳大利亚、 伊朗等， 威胁着人类的健康， 为社会造成了一定经济负担[7-9].

包虫病的传播需要中间宿主(羊、 牛、 猪、 马、 骆驼、 多种野生动物和人)和终末宿主(犬、 狼、 狐狸等肉食动物). 感染来源一般为患病或带虫犬等肉食动物.易感动物常因食入被犬粪便污染的饲草或饮水而感染； 将废弃的患病脏器喂犬， 可造成犬与羊等动物之间循环感染,人接触包虫卵也可被感染[10].

目前， 对包虫病的研究文献大多是医学方面的， 从数学建模方向研究包虫病的文献较少. 文献[11] 建立了包虫病在人畜之间传播的数学模型， 分析了影响疾病传播和控制的关键因素. 文献[12]研究了一类具有饱和发生率的包虫病模型， 讨论了平衡点的稳定性， 对疾病给出一些控制策略. 文献[13]提出了一个确定性常微分方程传染病模型， 研究了新疆地区包虫病的传播. 文献[14]建立了一个具有两个斑块的常微分方程模型， 研究了狗在两斑块间的扩散对包虫病传播的影响. 文献[15]研究了包虫病在红狐狸中的传播. 文献[16] 表明如果对带狂犬病病毒的犬类不进行控制， 将会对包虫病非流行区带来危害. 带病的狗是包虫病非流行地区的一个主要危害， 因此研究狗的扩散对包虫病的影响非常重要.不同于文献[14]， 本文考虑某区域内狗的扩散， 建立偏微分方程模型. 由文献[13]知， 人的加入并不影响模型的动力学行为， 人是最终中间宿主， 人感染包虫病之后， 不会再传染给其他人或动物， 因此该模型只考虑狗和家禽两个种群， 而不考虑人的因素. 利用线性化方法， 参考文献[17]， 研究了连接无病平衡点与地方病平衡点的最小波速问题， 证明了地方病平衡点的局部稳定性.

1 模型的建立

把狗和家禽两个种群均分成两个仓室： 易感者类和染病者类.SD(x,t)和ID(x,t)分别表示点x处，t时刻狗的易感者和染病者数量.SL(x,t)和IL(x,t)分别表示点x处， 时刻t时家禽的易感者和染病者数量， 并假设包虫卵的数量与染病狗的数量成正比. 假设A1,A2分别为新生狗和家禽的数量，β1为染病家禽对易感狗的传染率，β2为染病狗对易感家禽的传染率，m1,m2分别为狗和家禽的自然死亡率，σ为染病狗的恢复率，α1,α2分别为易感狗和染病狗的扩散率. 建立包虫病传播模型

(1)

其中，t>0,x∈Ω. 具有Neumann 边界条件

t>0,x∈∂Ω.(2)

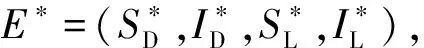
如果模型(1)存在行波解， 则其形式为

(SD(x,t),ID(x,t),SL(x,t),IL(x,t))=

(SD(z),ID(z),SL(z),IL(z)),

z=x-ct.

故模型(1)满足方程组(3)

(3)

(4)

2 最小波速

研究连接E0与E*的最小波速问题， 假设R0>1, 则式(4)的解应满足边界条件

与同时代人相比，何晏留存到今天的文字并不算少，除了这封奏章，他还写过一篇《景福宫赋》，同样是四平八稳，文笔辞藻样样都到位，只不过读起来跟炒菜没放盐似的，总感觉缺点什么。

特征方程为

Q(λ)P(λ)=0,(5)

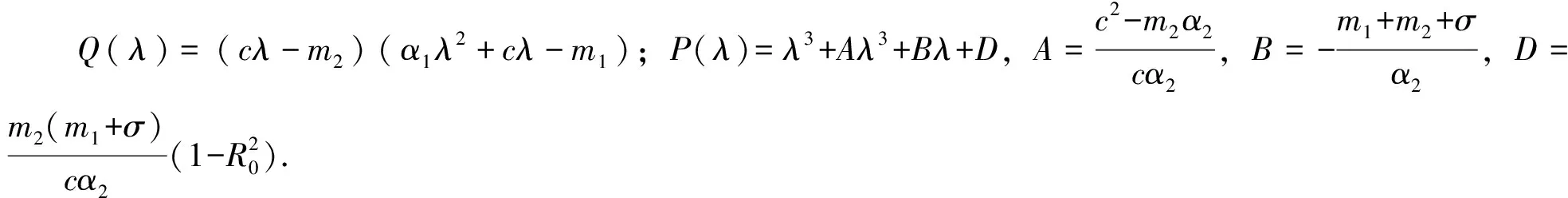
(6)

3 稳定性分析

研究地方病平衡点E*的稳定性， 首先做变换， 令

并设

S1(x,t)=s1eαt+in x,I1(x,t)=i1eαt+in x,

S2(x,t)=s2eαt+in x,I2(x,t)=i2eαt+in x,(7)

式中：s1,i1,s2,i2为常数； ein x为有界周期函数；n为波数.α的实部Reα的符号决定平衡点E*的稳定性. 如果Reα<0， 则E*是稳定的， 如果Reα>0， 则E*不稳定. 把式(7)代入式(1)中得

(α+m2)(α3+b1α2+b2α+b3)=0,(8)

其中

显然式(8)有一负根α=-d， 且bi>0(i=1,3). 记

则

由Routh-Hurwitz 判据知式(8)的所有根均具有负实部， 即地方病平衡点E*局部渐近稳定.

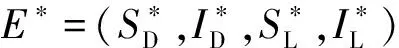
4 数值模拟

通过数值拟合来研究参数对包虫病传播及最小波速的影响.选取参数β1=5.8×10-8,β2=6.89×10-8,α1=0.005,α2=0.01,A1=2×105,A2=1.05×108,m1=0.08,m2=0.33,σ=2. 计算得最小波速为c*=0.108 7 km·year-1. 行波解见图 1.

图 1 ID(x,t)的行波图Fig.1 The traveling wave of ID(x,t)

图 2 显示了参数A1,σ,α1,α2对包虫病传播速度的影响. 由图 2 可以看出A1和σ的影响比α1和α2的要大.α1与α2仅影响行波的传播速度， 而A1和σ不仅影响行波的传播速度， 还影响行波的级数. 图 2 表明限制狗的扩散能减小包虫病的扩散速度， 但是不能消灭包虫病.

图 2 不同参数对ID(x,t)的影响Fig.2 The influence of different parameter values on ID(x,t)

图 3 显示α2比σ,A1,A2对最小波速c*的影响大， 即染病狗的扩散率是影响包虫病传播的最重要因素， 因此限制狗的活动对控制包虫病至关重要.σ对c*的影响仅次于α2， 随着σ的连续增加，c*不断减少. 通过增加对狗打驱虫剂的频率， 可以减少c*的值， 从而减小包虫病的扩散速度. 降低狗的出生率A1也有利于控制疾病传播.

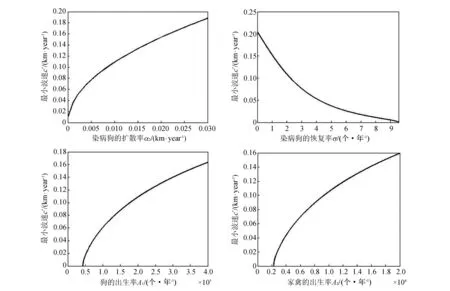
图 3 不同参数对最小波速c*的影响Fig.3 The influence of different parameter values on the minimum wave speed c*

5 结 论

本文研究了狗的扩散对包虫病传播的影响， 建立了反应扩散模型. 给出了行波解的最小波速和地方病平衡点的稳定性， 并对参数做了敏感性分析. 数值模拟表明控制染病狗的扩散， 增加对狗打驱虫剂的频率， 降低狗的出生率都对控制包虫病有利， 所得结论与文献一致.

[1] Yang Shijie, Wu Weiping, Tian Tian, et al. Prevalence of cystic echinococcosis in slaughtered sheep as an indicator to assess control progress in emin county, Xinjiang, China[J]. Korean Journal of Parasitology, 2015, 53(3): 355-359.

[2] Jia Wanzhong. Current progress on prevention of hydatid disease in China[J]. Veterinary Orientation, 2011, 6: 30-33.

[3] Li Tiaoying, Qiu Jiamin, Yang Wen, et al. Echinococcosis in Tibetan populations, western Sichuan Province, China[J]. Emerging Infectious Diseases, 2005, 11: 1866-1873.

[4] Yu Senhai, Wang Hu, Wu Xiaohong, et al. Cystic and alveolar echinococcosis: an epidemiological survey in a Tibetan population in southeast Qinghai, China[J]. Japanese Journal of Infectious Diseases, 2008, 61: 242-246.

[5] 温浩， 徐明谦. 实用包虫病学[M]. 北京： 科学出版社， 2007.

[6] 蒋次鹏. 我国包虫病流行近况[J]. 地方病通报， 2002, 17(3): 77-79.

Jiang Cipeng. Current progress of hydatid disease in China[J]. Endemic Diseases Bulletin, 2002, 17(3): 77-79. (in Chinese)

[7] Mastrandreaa S, Stegelb G, Piseddua T, et al. A retrospective study on burden of human echinococcosis based on Hospital Discharge Records from 2001 to 2009 in Sardinia, Italy[J]. Acta Tropica, 2012, 123: 184-189.

[8] Thompson R C A, Jenkins D J. Echinococcus as a model system: biology and epidemiology[J]. International Journal for Parasitology, 2014, 44: 865-877.

[9] Ebrahimipour M, Budke C M, Najjari M. Bayesian spatial analysis of the surgical incidence rate of human cystic echinococcosis in north-eastern Iran[J]. Acta Tropica, 2016, 163: 80-86.

[10] 王舂江, 李金岭, 吕广国, 等. 包虫病的流行过程、 症状及危害[J]. 兽医导刊, 2011, 6： 24-25.

Wang Chunjiang, Li Jinling, Lv Guangguo, et al. The epidemic process, the symptoms and harm of hydatid disease[J]. Veterinary Orientation, 2011, 6: 24-25. (in Chinese)

[11] 赵瑜, 康云. 包虫病传播的数学模型及控制策略研究[J]. 中国动物传染病学报, 2011, 19(4): 81-86.

Zhao Yu, Kang Yun. Mathematical modelling and controlling of echinococcosis spread[J]. Chinese Journal of Animal Infectious Diseases, 2011, 19(4): 81-86. (in Chinese)

[12] 杜守洪, 王蕾, 张学良, 等. 一类具有饱和发生率的包虫病传播模型研究[J]. 数学的实践与认识, 2013, 43(20): 269-273.

Du Shouhong, Wang Lei, Zhang Xueliang, et al. A echinococcosis model with saturation Incidence[J]. Mathematics in Practice and Theory, 2013, 43(20): 269-273. (in Chinese)

[13] Wang Kai, Zhang Xueliang, Jin Zhen, et al. Modeling and analysis of the transmission of echinococcosis with application to Xinjiang Uygur Autonomous Region of China[J]. Journal of Theoretical Biology, 2013, 333: 78-90.

[14] Wang Kai, Zhang Xueliang, Teng Zhidong, et al. Analysis of a patch model for the dynamical transmission of echinococcosis[J]. Abstract and Applied Analysis, 2014， 2: 1-13.

[15] Lewis F I, Otero-Abad B, Hegglin D, et al. Dynamics of the force of infection: insights from echinococcus multilocularis infection in foxes[J]. PLOS Neglected Tropical Diseases, 2014, 8(3): e2731.

[16] Giraudoux P, Pleydell D, Raoul F, et al. Transmission ecology of Echinococcus multilocularis: what are the ranges of parasite stability among various host communities in China? [J]. Parasitology International, 2006, 55(Suppl): S237-S246.

[17] Maidana N A, Yang H M. Spatial spreading of West Nile Virus described by traveling waves [J]. Journal of Theoretical Biology, 2009, 258: 403-417.