牵引回流对计轴设备的影响分析

王梓丞, 张亚东, 郭 进, 罗 蓉

(1.西南交通大学信息科学与技术学院,成都 611756； 2.北京城建设计发展集团股份有限公司,北京 100037)

计轴系统作为轨道区段占用检查设备通过计算进入区段与离开区段的车轴数来判断列车的占用及出清[1]。在我国，轨道电路是自动闭塞系统的主要设备，但针对计轴器的研究与探讨仍然是轨道交通领域的一个热点问题。文献[2]首次提出了利用计轴设备实现自动站间闭塞的设计思想。文献[3]考虑到移频轨道电路易受特长隧道独特环境的影响，提出了隧道内计轴加环线自动闭塞系统的设计方案。文献[4]针对山区铁路道床电阻较低的特殊地质环境，提出了采用计轴设备加轨道电路自动闭塞制式和设置接地降阻系统的解决方案。可见，计轴设备因其无需绝缘节、工作性能不受道床影响、适用于长区段等优点，适合在轨道交通领域中推广[5]。

主流的计轴传感器技术主要包括轮幅和轮缘2种检测方式[6]。轮幅式计轴传感器虽然技术成熟，但牵引回流磁力线方向与计轴传感器磁场路径相同，其电流变化导致磁场变化会影响计轴器计数[7]。相对的，轮缘式计轴器其感应线圈产生的磁场方向与机车牵引回流磁场方向垂直，理论上可以降低牵引回流对车轮检测的影响[8]。然而，目前针对牵引回流对两种类型计轴器影响的分析仍然处于空白阶段。事实上，在计轴器的现场使用过程中仍然发生过一些因牵引回流影响计轴设备，造成轨道区段红光带的现象[9]。随着轨道交通的发展，列车质量及速度会不断增加，牵引回流也将随之增大，对计轴器造成的影响也会更加严重。

Simplorer软件同时具备对Simulnk及Maxwell的接口，易于实现二者的联合仿真[10，11]。因此，通过建立计轴器的Maxwell三维模型以及牵引供电系统的Simulnk仿真模型，并基于Simplorer平台进行联合仿真，分析两种不同类型计轴器受牵引回流的影响。

1 基于Ansoft Maxwell的计轴设备仿真模型

计轴设备主要由钢轨、励磁线圈、磁芯、感应线圈、空间载体及车轮(有车)组成，其基本结构及尺寸如图1所示。两种计轴设备除尺寸不同外，在结构上最大的区别是：轮幅式计轴器的激励/感应线圈分别安装在钢轨两侧(双侧计轴器)，而轮缘式计轴器的激励/感应线圈统一安装在钢轨一侧(单侧计轴器)，且有两个感应线圈。

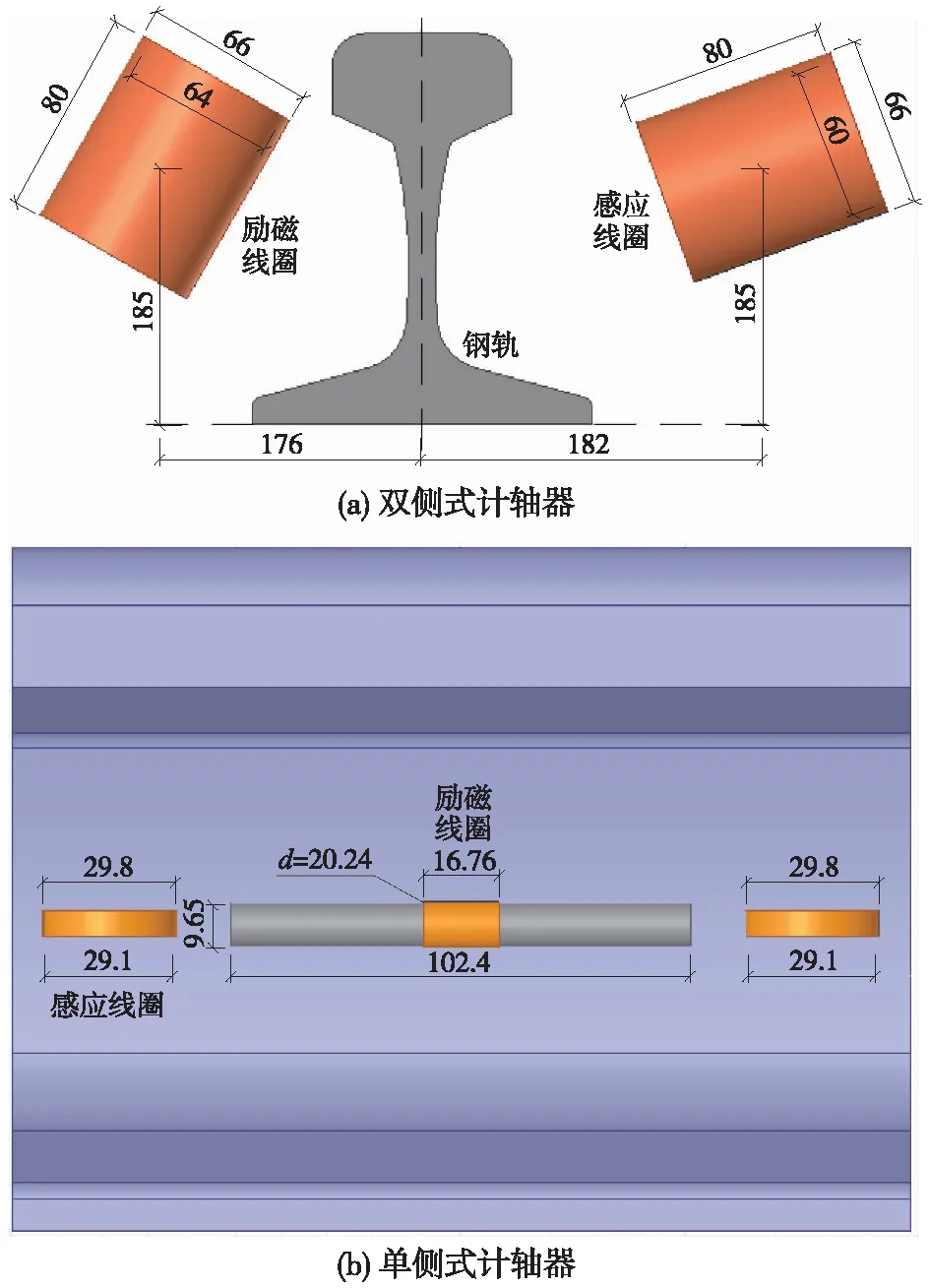
图1 计轴器的基本结构(单位：mm)

为了分析双侧/单侧计轴器的工作特性及其受牵引回流的影响，在Ansoft Maxwell 16.0中建立计轴器的三维仿真模型。其中，双侧计轴器的励磁线圈匝数N1=300，接收线圈匝数N2=1 440；单侧式计轴器的励磁线圈匝数N3=24，接收线圈匝数N4=32，材料均选用软件自带的“copper”材料；钢轨原型采用50 kg/m型号进行建模，车轮采用客运列车常用轮对RD33型轮对，车轮和钢轨都是铁磁性物质，模型中钢轨及车轮选用同一材料：相对磁导率μ=7 000，电导率为1.031×107S/m，相对介电常数为2.55。两种计轴器均用铁氧体磁芯置于励磁线圈中心，但尺寸不同，双侧计轴器的磁芯长度l1=60 mm，半径r1=15 mm，单侧计轴器磁芯长度l2=102.4 mm，半径r2=4.875 mm。

计轴器的三维模型建立好后，对模型进行网格剖分，结果如图2所示。由于计轴器各部件的尺寸大小不同，在进行网格剖分时针对不同部件分开进行，如励磁/接收线圈的尺寸较小且对精度要求较高，因此网格剖分更精细，对于车轮和钢轨，为了节省计算资源，网格剖分比较稀疏。此外，考虑到整个车轮只有轮缘以及靠近钢轨的一部分会对计轴传感器周围的磁场产生影响，因此模型中只截取了车轮的一部分进行仿真。

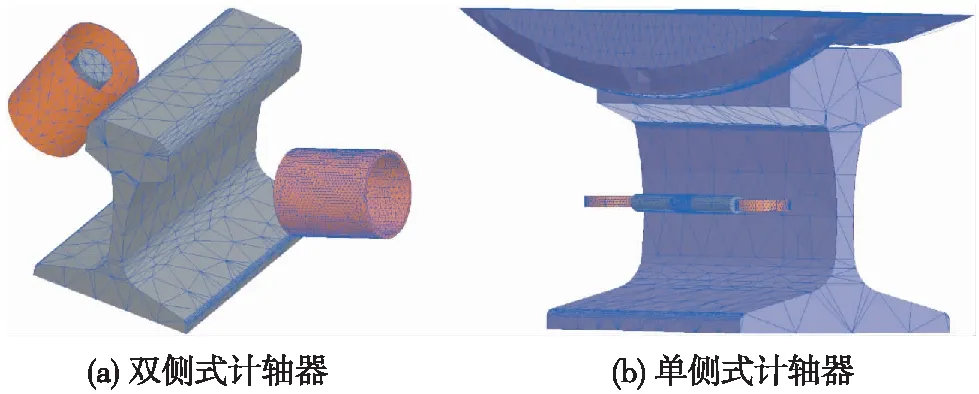
图2 计轴器三维模型的网格剖分

2 基于Simulink的牵引供电系统仿真模型

铁路牵引供电系统由外部电源、牵引变电所、接触网和电力机车组成，采用工频50 Hz交流电，额定电压为27.5 kV。本文基于Simulink建立了牵引供电系统的仿真模型，包括牵引网和CRH2动车组两部分。

2.1 牵引网仿真模型

我国电气化铁路复线牵引网的几何结构如图3所示，系统由接触线(T)、承力索、正馈线(AF)、保护线(PW)、钢轨(R)以及贯通地线等组成，其中，接触线和承力索由吊弦连接，为了简化计算在仿真模型中将其合并等效，贯通地线埋于地下，与其他架空导线间的互阻抗忽略不计。此外，不考虑钢轨不平衡影响，将2根钢轨等效为处于二者中间的单根导体。最终，得到复线牵引网8导体等值电路：接触线(T1，T2)、正馈线(AF1，AF2)、保护线(PW1，PW2)、钢轨(R1，R2)。

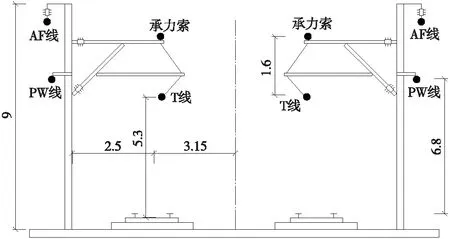
图3 牵引网几何结构(单位：m)

牵引网平行多导体单位长度阻抗参数(Ω/km)可用Carson公式计算[12]

(1)

式中，Zii、Zij分别为导线自阻抗和互阻抗；f为电流频率；ri、r地分别为导线自身和大地电阻；Ri为导线半径，cm；dij为导线间距，m；σ为大地电导率。

单位长度分布电容参数可用电位系数法计算，其自电位系数和互电位系数(km/F)可表示为[13]

(2)

式中，ε0为空气介电常数；Dij为导体与导体镜像间距；hi为导体离地高度。

然而，钢轨因其形状不规则不具备半径Ri，因此阻抗参数无法用式(1)求出。对此，采用二维电磁场有限元法对钢轨等效半径进行提取，计算同样在 Ansoft Maxwell中完成。在钢轨二维几何模型外围设置一半径r0的圆作为参考地，并进行静电场分析获取C参数。当钢轨和外部圆达到一定距离时空间电位分布接近圆形截面导体的电位分布，此时，可根据同轴导体电容计算公式C=2πε0/ln(r0/rrail)反推出钢轨的等效半径[14]。仿真结果如图4所示，计算求得钢轨等效半径为19.85 mm。最后，将等效半径代入式(1)求取钢轨的自阻抗、互阻抗等参数。

图4 钢轨等效半径计算结果

基于解析-数值方法求得牵引供电多导体单位长度参数后，在Simulink中用π型等效电路模拟牵引网，牵引网按1 km长度进行了子网划分，子网仿真模型如图5所示。

2.2 CRH2型动车组

我国高速铁路动车组主要采用交-直-交变频方式，该系统主要包括受电弓、断路器、牵引变压器、变流器、中间直流环节、逆变器、三相异步电机，其结构如图6所示。

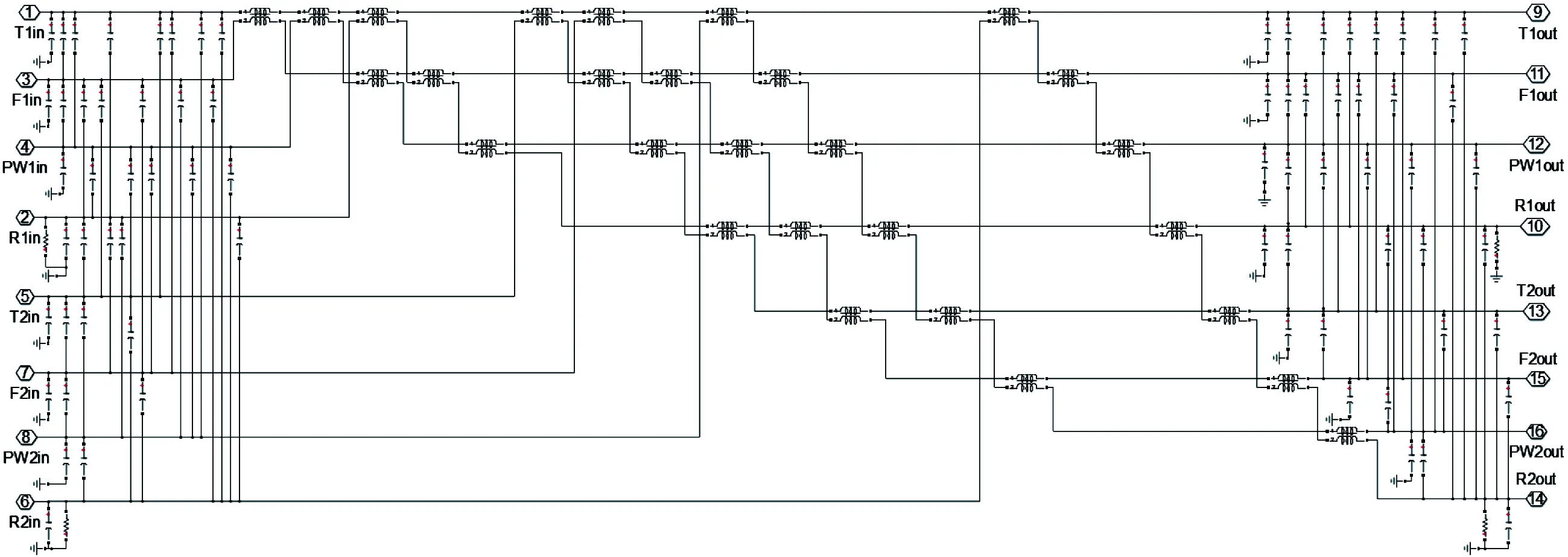
图5 1 km牵引子网仿真模型

图6 CRH2型动车组主电路示意

根据CRH2型动车组的结构在Simulink建立模型如图7所示。一般情况下，机车变流器后面的部分其电气参数的变化有其自身闭环控制系统约束，可以视作一个恒定负载，负载电阻值由输出功率确定：R=U2/P。仿真参数为：交流侧输入电压1 500 V，网侧电感LN=2 mH，网侧电阻RN=0.006 8Ω，直流侧支撑电容为C=2 200 F，三电平整流器的载波频率为fs=1 250 Hz。

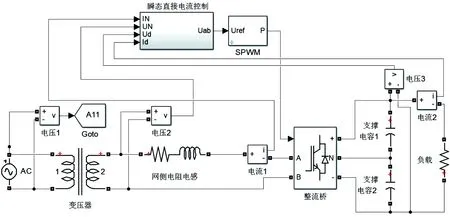
图7 CRH2型动车组仿真模型

图7中，CRH2型动车组采用单极性三电平SPWM调制和瞬态直接电流控制技术，其计算公式为[15]

(3)

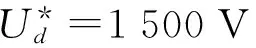
在Simulink中建立瞬态直接电流控制仿真模型如图8所示。

最终，在Simulink中搭建如图9所示的牵引供电系统仿真模型，该模型包含牵引网和动车组两部分。图中，牵引网左右供电臂各30 km，每15 km设置自耦变压器(Auto Transformer， AT)，将其中性点与钢轨相联并且并联于牵引网中。15 km牵引网被切割为15个牵引子网，每个子网包含1 km的牵引供电多导体模型，其中，牵引多导体采用2.1节所述方法计算其单位长度参数，并用图5所示π型等效电路模拟。此外，采用220 kV外部电源为牵引变压器一次侧供电，牵引变压器二次测的额定电压为27.5 kV。CRH2型动车组按照本节所述方法进行建模。

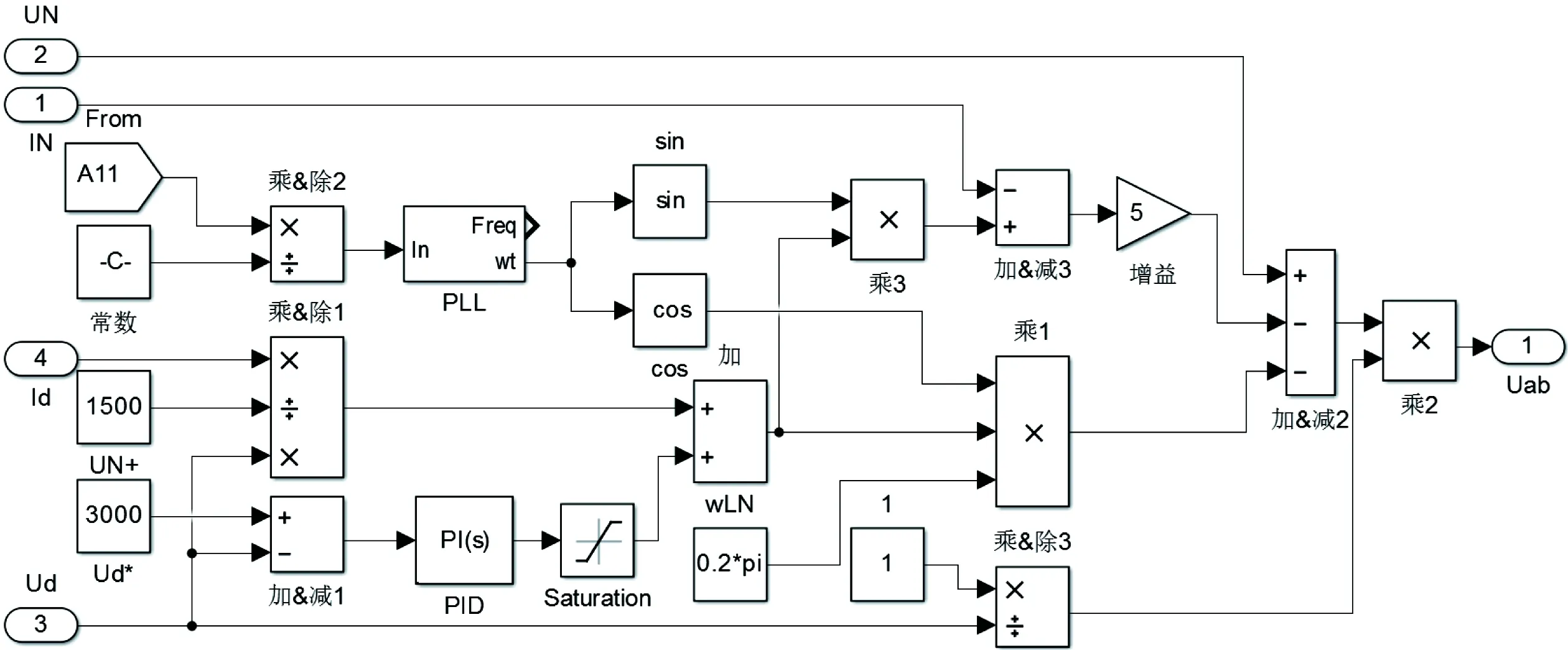
图8 瞬态直接电流控制仿真模型

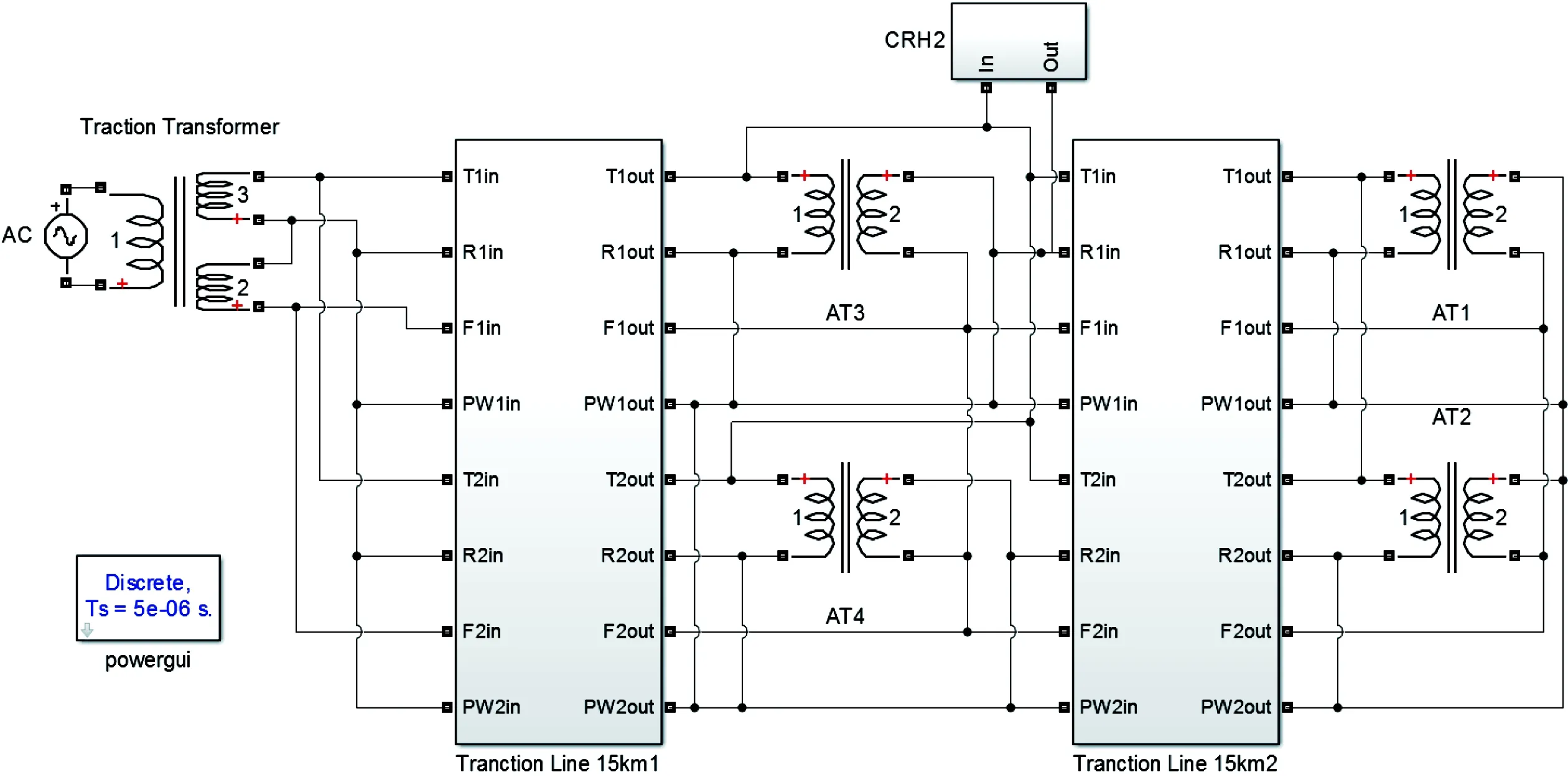
图9 牵引供电系统仿真模型

3 实例仿真

首先，为了分析和对比两种计轴器的工作性能，对无车轮和有车轮时计轴器周围磁场、感应线圈上感应电动势的变化进行仿真分析；其次，基于Simplorer软件联合计轴器的Maxwell三维仿真模型和牵引供电系统的Simulink模型，分析牵引回流对计轴器的影响。

3.1 计轴器工作状态的仿真及对比分析

在铁路现场，计轴器被安装在铁路区段的首末两端，当列车从区段的一端驶入时，计轴器周围的磁场分布情况发生变化，使感应线圈中的感应电压降低，从而产生计轴信号；当列车驶出时，另一计轴器产生相应的计轴信号，通过对比区段两端的计轴信号就可以判断列车在该区段的占用情况以及列车的行驶方向。

双侧计轴器的励磁信号电压为28.28 V，信号频率为31.25 kHz；单侧计轴器的励磁线圈通入的电流幅值为59 mA，电流频率为250 kHz。根据所建立的计轴器三维模型及给定的参数，对有车及无车两种情况计轴器周围的磁场进行仿真，结果如图10所示。对于双侧计轴器而言，大部分磁感应线会经钢轨所在的磁通路径闭合，图10中感应线圈处的磁感应强度远小于经过钢轨的磁感应强度；另一方面，车轮和钢轨都属于铁磁物质，所以更多的磁感应线会通过车轮和钢轨所在的路径闭合，导致有车轮时感应线圈处的磁感应强度更小。单侧计轴器的情形与此类似，当有车轮经过时，一部分磁通会通过车轮所在的路径闭合，导致感应线圈中的磁通量下降。感应线圈磁感应强度的变化会直接影响感应电压的大小，感应线圈感应电压的仿真结果如图11所示，其中，双侧计轴器感应电压峰值分别为10.46 mV(无车)和6.02 mV(有车)，单侧计轴器2个感应线圈上的感应电压幅值相同但方向相反，其峰值分别为1.9 mV(无车)和0.11 mV(有车)。

图10 无车/有车时计轴器周围磁感应线云图

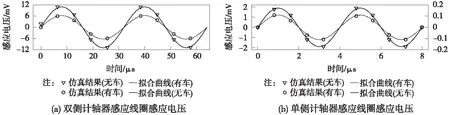
图11 无车/有车时计轴器感应线圈感应电压仿真结果

3.2 计轴器受牵引回流的影响分析

计轴器安装在钢轨侧，势必会收到牵引回流的影响，而两种计轴器安装方式及结构不同，所受影响的程度也不相同。为了研究牵引回流对计轴器的影响，在Simplorer平台上联合牵引供电系统的Simulink模型及计轴器的三维Maxwell模型进行仿真，其仿真原理如图12所示。

图12 牵引供电系统-计轴器联合仿真原理

首先，从牵引供电系统的Simulink模型中获取列车运行时的牵引回流；在Simplorer平台中设置电流控制电流源(Current Controlled Current Source， CCCS)，将牵引回流转变为计轴器的电流激励；将计轴器Maxwell模型中钢轨的2个横截面分别作为电流激励的输入、输出施加面，最后计算由牵引回流在计轴器周围产生的磁场以及感应线圈中感应电压的大小。基于Simplorer的牵引供电系统-计轴器联合仿真模型如图13所示。

图13 基于Simplorer的联合仿真模型

牵引供电系统、计轴器的参数按照第2节设置，在此基础上对联合模型进行仿真，在Simplorer平台中测量得到电流峰值为57.23 A的牵引回流如图14所示。

图14 牵引回流仿真结果

在Ansoft Maxwell软件中计算钢轨通入牵引回流时计轴器周围磁矢量的分布情况，结果如图15所示，为了更好地分析牵引回流造成的影响，与计轴器自身激励信号产生的磁场进行了对比。可见，由于励磁线圈和接收线圈分别安装在钢轨两侧，双侧计轴器激励信号的磁力线与牵引回流的磁力线重合，因此受牵引回流的影响较大；而单侧计轴器磁力线方向与牵引回流的磁力线垂直，相较于牵引回流，激励信号在2个感应线圈处的磁感应强度大小相等，方向相反。因此，虽然感应线圈也会因牵引回流的影响产生感应电动势，但两个线圈中感应电压峰值和方向均一致。在牵引回流条件下，对计轴器感应线圈上的感应电压进行仿真，得到如下结果：双侧计轴器干扰电压峰值为3.36 mV；单侧计轴器为0.754 mV，且两感应线圈上的干扰电压峰值和方向都相同。

图15 激励信号/牵引回流时计轴器周围磁矢量的分布

4 结论

(1)在Ansoft Maxwell中建立了计轴器的三维仿真模型，对计轴器周围磁场的分布及感应线圈感应电压进行了计算：对于双侧计轴器其感应电压峰值分别为10.46 mV(无车)和6.02 mV(有车)，而单侧计轴器为1.9 mV(无车)和0.11 mV(有车)。

(2)在Simulink中建立牵引供电系统的仿真模型，根据Carson公式对牵引供电多导体的单位长度阻抗参数进行了计算，对于非规则横截面导体采用二维有限元对其等效半径进行了提取：R等效=19.85 mm。

(3)通过Simplorer平台联合计轴器的Maxwell模型和牵引供电系统的Simulink模型分析牵引回流对计轴器的影响，双侧计轴器受牵引回流的影响较大，干扰电压峰值达3.36 mV，而单侧计轴器由于磁力线方向与牵引回流的磁力线垂直，因此所受影响较小。

[1] 闻崇义.浅谈计轴技术的发展和运用[J].铁路通信信号工程技术，2007(2):21-22.

[2] 付军.利用计轴设备实现一体化计轴自动站间闭塞功能[J].铁道标准设计，2004(9):96-98.

[3] 薛长虹.青藏铁路关角特长隧道内自动闭塞设计探讨[J].铁道标准设计，2012(4):127-134.

[4] 喻矿强.襄渝线山区铁路信号系统特殊问题解决方案[J].铁道标准设计，2012(4):124-126.

[5] 王力.计轴设备在轨道交通信号领域的应用[J].铁道通信信号，2011(1):20-22.

[6] Martin Rosenberger. Future challenges to wheel detection and axle counting [J]. Modern Wheel Sensor Systems，2011(9):37-43.

[7] 弓剑. 各类电子式计轴设备工程应用浅析[J].铁道通信信号，2011(6):34-37.

[8] Ali Zamani，Ahmad Mirabadi. Analysis of sensor orientation in Railway axle counters， using Response Surface Methodology [C]∥Proceedings of 5th Symposium on Advances in Science & Technology，Iran， 2011：12-17.

[9] 蒋晶，龙讯，钟志辉.浅谈如何降低牵引电流感应对计轴设备的影响[J].信息通信，2015(1):278.

[10] 康洪铭，李光升，魏宁，杨亚丽，黎毅.装甲车辆电源系统Simulink与Simplorer联合仿真[J].电源技术，2013，37(10)：1862-1865.

[11] 杨钟鼎，周洁敏，姜春燕，周迪，杨东澄.基于Simplorer/Maxwell的多电飞机机电驱动系统仿真研究[J].重庆理工大学学报(自然科学版)，2016，30(2)：127-132.

[12] 李群湛，贺建闽.牵引供电系统分析[M].成都：西南交通大学出版社，2007.

[13] C R Paul. Analysis of Multi-conductor Transmission Lines， 2nd Edition[M]. New York：Wiley，2007.

[14] 刘欣，崔翔.电气化铁路接触网雷电感应过电压计算及其闪络概率研究[J].华北电力大学学报，2013，40(2)：10-16.

[15] 冯晓云.电力牵引-交流传动及其控制系统[M].北京：高等教育出版社，2009.