大轴重双线铁路路基结构动力学分析

尹紫红,赵丰年,高 雪

(西南交通大学土木工程学院,成都 610031)

1 概述

经济发展，交通先行。交通运输是保证经济稳增长的前提，在推进实施“三大战略”中起着引领性作用。近年来，地域间经济和社会的发展呈现出差异扩大化趋势，资源的地域矛盾越发突出，快速实现物资的空间移动成为解决矛盾的关键。重载铁路因其高效的运输效率、良好的经济效益而被幅员辽阔的国家广泛采用。山西中南部铁路通道的建设运营是重载铁路的里程碑，它标志着我国重载铁路所需理论和技术的成熟，并能将其运用在具体工程实践中[1]。“一带一路”作为国家“三大战略”之一，其中的“丝绸之路经济带”沿线有着丰富的自然资源、矿产资源、能源资源、土地资源和宝贵的旅游资源[2]，但由于交通条件的限制，经济发展水平与两端的经济圈存在巨大差异，故建设通往欧洲的重载货运走廊就显得尤为迫切。

重载铁路荷载作用具有大轴重、高频次、重复等特点，为保证列车的平稳运行，学者们研究分析作为承受这部分动荷载的路基在满足承载力和变形的要求上就显得极为重要。如：董亮[3]根据建立的单线三维有限元模型分析了动应力沿路基纵向、横向及深度方向的变化；郭抗美[4]根据弹性理论建立单线轨道-路基三维有限元模型，分析不同荷载水平和基床结构形式下路基动应力分布和衰减规律；肖世伟[5]通过分析大秦线和九江线试验数据，验证了单线模型计算列车荷载产生的应力是合适的，同时也验证了相邻转向架共同作用计算动应力是合理的。然而学者们大多采用单线铁路进行路基受力变形研究，对双线并行重载铁路的研究鲜有涉及，尤其是线间距对路基受力影响方面。因此掌握并行线路中心线处路基力学传递规律和动应力影响范围，是对并行线路线间距设计的先决条件。

本文借助于轨道-路基一体化模型，针对线间距、基床表层弹性模量和轴重因素，分析重载作用下线间路基动力响应和力学传递规律，为不同轴重下双线并行重载铁路线间距、填料设计研究提供技术支持和理论指导。

2 三维有限元模型建立

2.1 模型假设

采用线弹性本构理论，建立基于广义胡克定律的轨道-路基三维有限元计算模型[6][7]。假定各层是连续的、完全弹性的、均匀的和各向同性的理想弹性体，各层的结合状况是连续的，不出现脱空现象[8]。轨道结构计算采用弹性点支承连续梁模型，不考虑轨道所受横向、纵向作用[9-11]。根据重载铁路扣件刚度设计规范，本文中扣件选用垂向单刚度为37.5 kN/mm的双弹簧单元并联模拟[12]。

2.2 荷载条件

采用准静态计算方法，将列车静荷载经荷载系数换算后，如式(1)，简化为集中荷载施加在轨道结构上，然后依次向下传递。车辆模型采用不同重载车型，车体长12 m，轴重分别为30、35、40、45 t，荷载作用模式及位置如图1所示。

Pd=Ps(1+αυ)

(1)

式中Pd——动轴载，kN；

Ps——静轴载，kN；

α——速度影响系数，货车取0.004；

υ——行车速度，km/h，取120 km/h。

图1 车辆荷载分布位置

2.3 模型尺寸及材料力学参数

根据《铁路路基设计规范》(TB10001—2016)、《铁路路基极限状态法设计暂行规范》(Q/CR9127—2015)和《重载铁路设计规范》(报批稿)等设计规范[13]。钢轨采用75 kg/m轨，轨枕采用Ⅲ型混凝土轨枕并按1 667根/km铺设，轨枕尺寸为2.6 m×0.32 m×0.22 m，道床边坡坡度为1∶1.75，基床边坡坡度为1∶1.5，基床表层厚度为0.7 m，基床底层厚度为2.3 m[14]，路基模型全长20.4 m。基床表层选用A组填料或级配碎石，基床底层选用B组填料，路基本体选用C组填料[4]。模型各部分计算参数如表1所示。

表1 三维有限元计算参数

根据设定参数建立的三维有限元计算模型，如图2所示。该模型中X、Z、Y轴方向分别表示线路横向、纵向及线路深度方向。沿线路纵向两端面边界设置为Z向约束，X、Y方向自由，路基底部设置为三方向约束，路基边坡设置为自由[15]。

图2 三维有限元计算模型

3 路基动应力分析

本文中建立的有限元计算模型设置有线间距、轴重、基床表层弹性模量3个变量，采用单一变量分析不同轴重下线路中心线处沿深度方向的应力传递规律，不同线间距对应力传递规律的影响及基床表层弹性模量因素在应力传递中的影响效果，评价各变量在路基动态响应中的影响程度，并针对不同影响程度提出改善措施。图3、图4分别为轴重35 t、线间距4.2 m、基床表层弹性模量180 MPa三维有限元纵、横向断面应力云图。

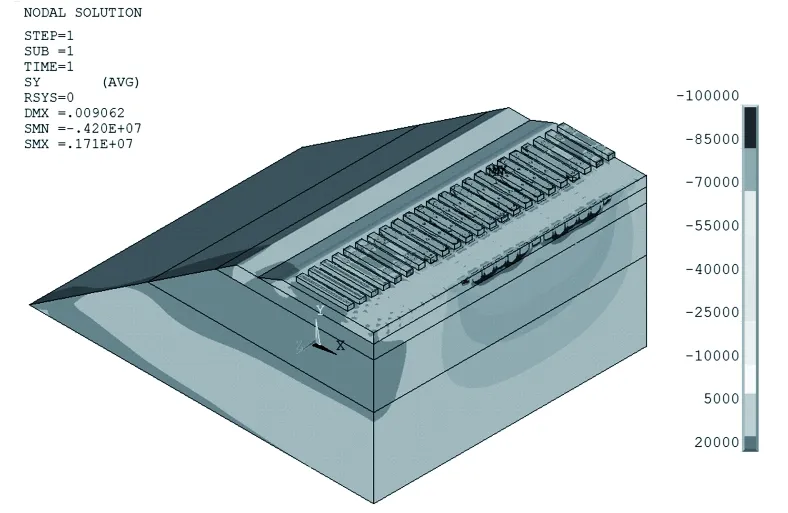
图3 双线四轴加载纵断面应力云图

图4 双线四轴加载横断面应力云图

3.1 模型假设

30 t轴重下，在外侧轨轴载作用位置处(减少应力叠加的干扰)，基床表面最大应力为76.03 kPa，与文献[3]中的计算结果78.28 kPa相比，误差2.87%；基床底层动应力衰减57.63%，与文献[3]中衰减64.97%相比，误差11.29%。35 t轴重下，在外侧轨轴载作用位置处，基床表层0.6 m深度处动应力65.68 kPa，与文献[4]中的67.45 kPa相比，误差2.63%。通过对比分析，以上误差都在容许范围内，可以验证模型的准确性。

3.2 不同轴重下路基动应力

不同轴重下线路中心线处路基动应力与轨道中心线处路基动应力分别如表2、表3所示。在线间距为4.2 m，基床表层弹性模量为180 MPa时，线路中心线基床表层处的动应力是轨道中心线处的22.43%，基床底层处为72.20%，路基本体处为108.53%。

在线路中心线处，不同轴重下路基动应力峰值都出现在1.0 m深度处，且轴重与动应力峰值呈线性正相关，比例系数为1.31。深度小于1.0 m时，动应力叠加的速率基本呈对数增长，深度大于1.0 m时，动应力的衰减速率基本呈线性减小。

线路中心线动应力沿深度方向衰减速率缓于轨道中心线，两者在1.864 m处达到相同的动应力幅值。随后，沿深度方向，同一深度处线路中心线应力幅值总是大于轨道中心线，如图5所示。

轴重为30、35、40、45 t时，经道床和基床应力消散后，车辆荷载在线路中心线3 m深度处产生的动应力与路基自重应力之比分别为0.37、0.44、0.50、0.56，如图5所示。

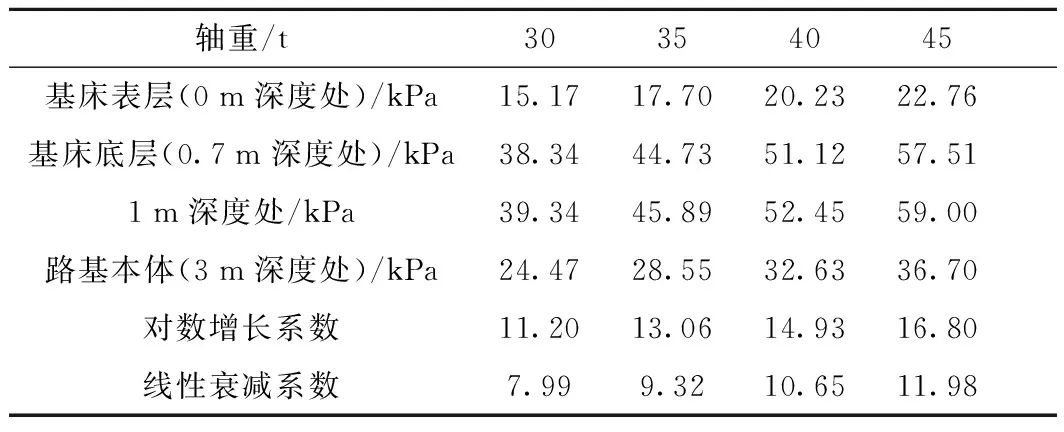
表2 不同轴重下线路中心线路基动应力

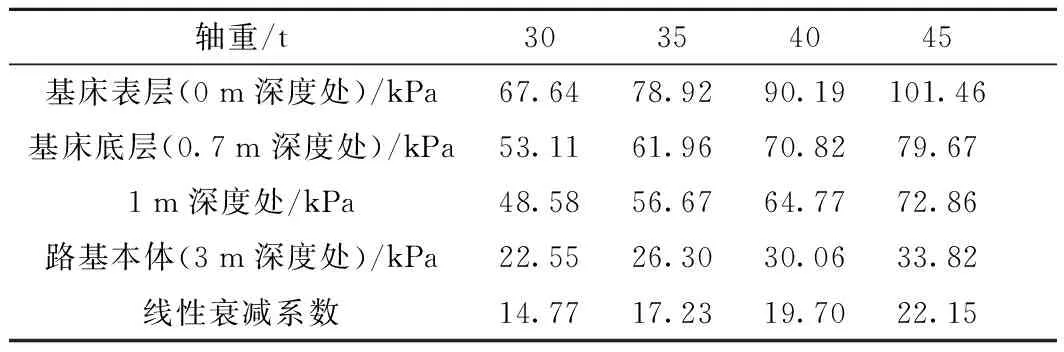
表3 不同轴重下轨道中心线路基动应力

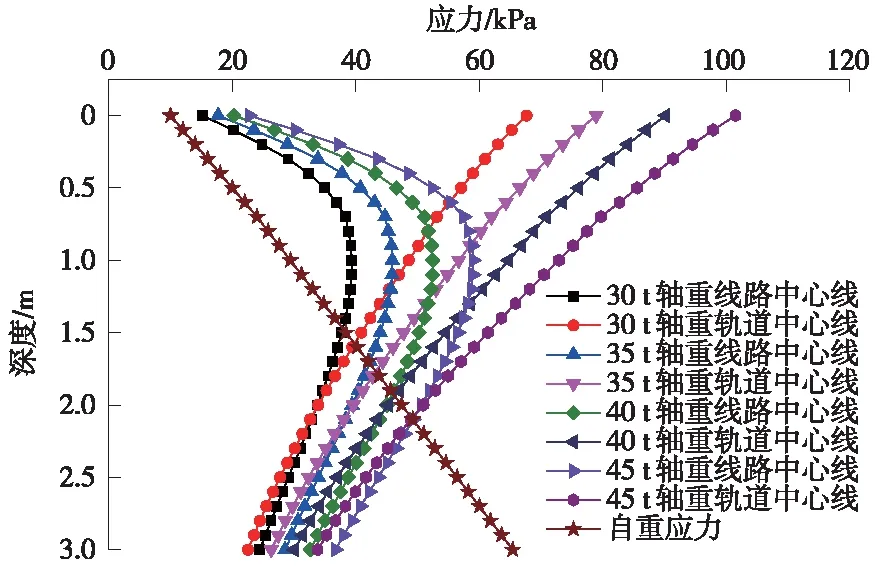
图5 不同轴载作用路基应力分布

3.3 不同线间距下路基动应力

不同线间距下，轴重35 t、基床表层弹性模量180 MPa的三维有限元动力计算结果如表4所示。线间距对线路中心线处路基动应力响应和传递规律影响明显，表4中数据经线性拟合后，线间距每增加0.2 m，应力峰值减小4.8 kPa，减小幅度在8.39%～11.52%，应力峰值深度位置增加0.15 m，增加幅度在12.5%～21.43%。

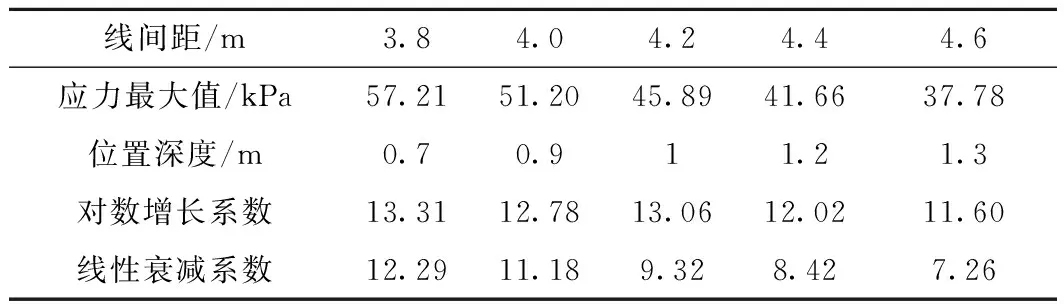
表4 不同线间距下线路中心线路基动应力

图6所示为线路中心线处沿路基深度方向动应力分布。线间距3.8 m时，动应力线性衰减系数为12.29；线间距每增加0.2 m，动应力线性衰减系数减少1.28；线间距4.6 m时，动应力线性衰减系数为7.26；线间距逐渐减小，路基动应力的衰减不断加快。

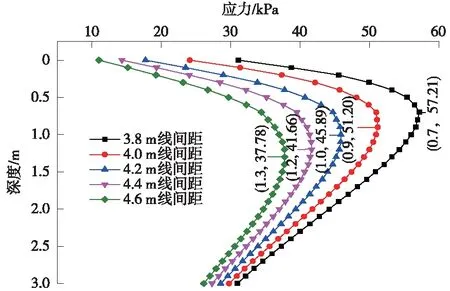
图6 不同线间距下路基应力分布

线间距对基床底层动应力在横向上的分布影响显著，如图7所示。线间距每减小0.2 m，线路中心线处基床底层动应力增加5.71 kPa。线间距越小，基床底层处线路中心线动应力越接近轨下动应力幅值，且由于轴载作用效果的叠加，内侧轨轨下动应力与外侧轨轨下动应力幅值差越大。

图7 不同线间距下基床底层应力横向分布

不同线间距下线路中心线处路基层动应力如表5所示。线间距3.8 m时，线路中心线处路基本体表面动应力损耗45.9%，削弱为30.95 kPa；线间距4.0 m时，线路中心线处路基本体表面动应力损耗41.66%，削弱为29.75 kPa；线间距4.2 m时，线路中心线处路基本体表面动应力损耗40.73%，削弱为28.52 kPa；线间距4.4 m时，线路中心线处路基本体表面动应力损耗30.92%，削弱为27.3 kPa；线间距4.6 m时，线路中心线处路基本体表面动应力损耗24.14%，削弱为26.11 kPa。线间距增大时，基床底层的动应力随之减小，基床底层对动应力的损耗值和衰减效率也相应减小。

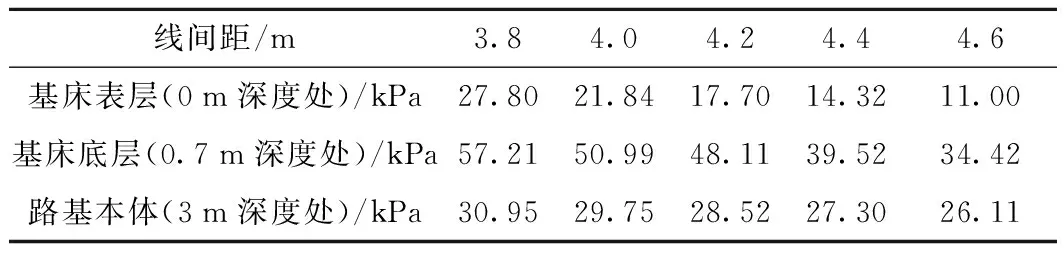
表5 不同线间距下路基层动应力

图8 不同线间距下路基本体应力横向分布

不同线间距对路基本体上的动应力横向分布影响程度不同，如图8所示，在线路中心线处影响显著。当线间距小于4.4 m时，线路中心线路基本体处出现动应力叠加，且线间距越小叠加效果越显著，线间距每减小0.2 m，动应力叠加1.22 kPa。当线间距大于4.4 m时，线路中心线路基本体处叠加效果微弱。

3.4 不同基床表层弹性模量下路基动应力

基床弹性模量对线路中心线动应力的影响效果如图9所示。基床表层弹性模量每增加50 MPa，动应力峰值增加0.38 kPa，变化幅度在8‰左右，动应力峰值位置深度的变化幅度在10%以内，基床表层模量的变化对应力峰值深度的影响较小，对应力幅值的变化影响不明显。

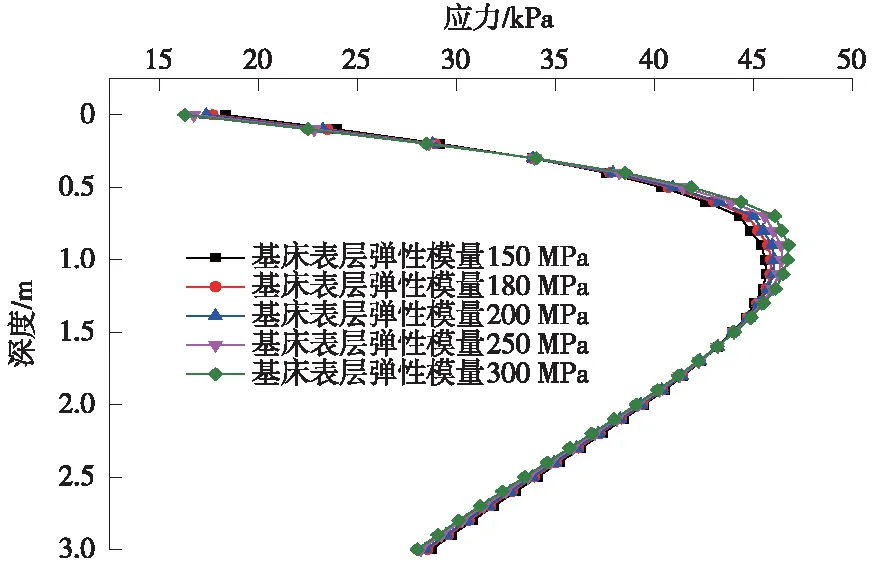
图9 不同基床表层模量下路基应力分布

不同基床表层弹性模量下，线路中心线处动应力对数增长系数在12.3～14.8，线性衰减系数在9.3～9.8，如表6所示。

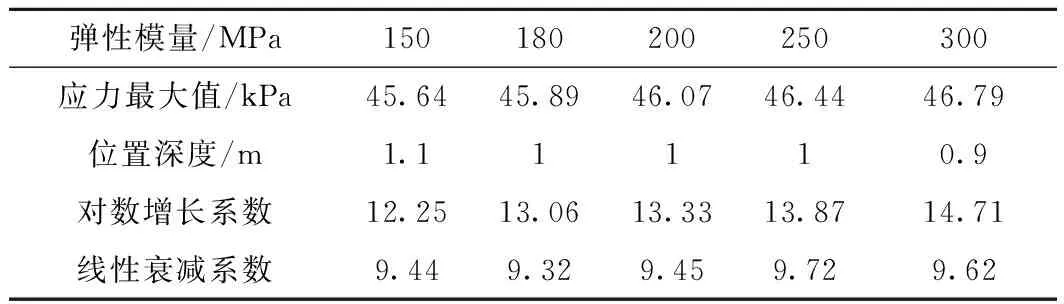
表6 不同基床表层弹性模量下线路中心线动应力

路基结构层动应力随基床表层弹性模量的变化如表7所示。表7中数据经线性拟合后，基床表层弹性模量每增加50 MPa，基床表层动应力减小0.67 kPa，减小幅度在3.65%～4.12%，基床底层动应力增加0.60 kPa，增加幅度在2.08%～2.27%，路基本体动应力减小0.24 kPa，减小幅度在0.83%～0.86%。

基床表层弹性模量为150、180、200、250、300 MPa时，基床底层动应力消散分别为35%、36%、37%、38%、39%。基床表层弹性模量越大，动应力消散效果越明显。

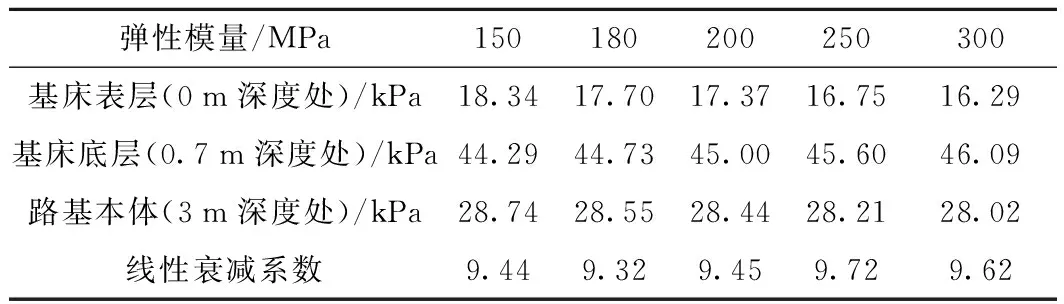
表7 不同基床模量下路基结构层动应力

4 结论

(1)在线路中心线处路基基床结构动应力沿深度方向先对数增长，在达到临界深度后线性减小，轨道中心线动应力则表现为沿深度减小。

(2)动应力峰值与线间距、基床表层弹性模量和轴重有关，线间距越小，轴重越大，动应力峰值越大；基床表层弹性模量增大，动应力峰值增大，但影响幅度较小；峰值位置深度主要与线间距有关与轴重无关，线间距越小动峰值位置出现越浅；线间距每增大0.2 m，线路中心线处动应力峰值减小4.8 kPa，峰值位置深度增加0.15 m。

(3)线间距小于4.4 m时，线路中心线处路基本体表面动应力大于轨道中心线处路基本体表面动应力，内侧轨下基床底层动应力叠加效果显著，线间距大于4.4 m时，则反之，对于线间距小于4.4 m的基床结构和路基本体，设计时应着重考虑线路中心线的动应力值。

(4)基床表层弹性模量对线路中心线处动应力衰减影响较小。

[1] 王宇嘉，徐利民，贾永刚，等.山西中南部通道重载列车运输试验及对线路设计的启示[J].铁道货运，2015(10)：27-31.

[2] 范建华.云南在“一带一路”国家开放战略中的重要地位与发展担当[J].大理学院学报，2015，14(3)：23-29.

[3] 董亮，赵成刚，蔡德钩，等.高速铁路路基的动力响应分析方法[J].工程力学，2008，25(11)：231-236.

[4] 郭抗美，王岩，叶庆志，等.重载铁路路基基床结构设计研究[J].铁道工程学报，2014，31(11)：1-5.

[5] 肖世伟，雷长顺.重载铁路路基荷载特征和路基动力响应分析[J].铁道工程学报，2014(4)：51-56.

[6] 王立娜.青藏铁路多年冻土区列车行驶路基振动反应与累积永久变形[D].哈尔滨：哈尔滨工业大学，2013.

[7] 刘晶磊，叶庆志，宋绪国，等.重载铁路路基荷载条件及动力特性研究[J].铁道工程学报，2015，32(2)：33-38.

[8] 岳蓓蓓.高速货运重载铁路有砟轨道及路基动应力分析[D].天津：河北工业大学，2015.

[9] 吕文强.大轴重重载铁路路基基床结构设计方法及技术标准研究[D].成都：西南交通大学，2015.

[10] 杨俊斌.弹性支承轨道结构参数研究[D].成都：西南交通大学，2008.

[11] 赵伟.单元板式无砟轨道伤损及纵向受力分析[D].成都：西南交通大学，2008.

[12] 杨露.基于无碴轨道结构静力性能的桥梁梁端变形容许值改进措施研究[D].长沙：中南大学，2013.

[13] 张立群，张丽娇.重载铁路单轮轴作用轨枕荷载分担规律研究[J].河北建筑工程学院学报，2016，34(2)：10-13.

[14] 常卫华.35.7 t轴重重载铁路轨道关键设计参数研究[J].铁道标准设计，2015，59(8)：47-50.

[15] 尹紫红，朱波，杨邦强，等.重载铁路路基动力响应的数值分析[J].路基工程，2016(5)：1-5.