高铁沿线地下水位动态变化引发的成层弱透水层固结研究

黄大中,李国和

(1.中国铁路设计集团有限公司,天津 300251； 2.轨道交通勘察设计国家地方联合工程实验室,天津 300251)

随着我国社会经济的快速发展，地下水资源的需求量大幅增加，超采地下水导致了区域性的地面沉降灾害，其中华北平原和长三角地区属于地面沉降严重影响区[1]，这些地区同时也是高速铁路网最为密集的地区，包括京沪高速铁路、京津城际铁路、津秦客专、沪宁客专、沪杭客专等。高速铁路对工后沉降的要求十分严格，严重的地面沉降将直接威胁高速铁路的平稳安全运营[2-4]。

地下水开采引发的地面沉降主要包括含水层的压缩变形和弱透水层固结变形[5]。在华北平原和长三角的大部分地区，通常分布着大量的成层弱透水层，由于弱透水层土体多为粉质黏土、黏土等软土，压缩性较大，因此弱透水层的固结变形是地面沉降的主要组成部分[6-7]。很多学者针对地下水位下降引发的弱透水层固结问题进行了研究。骆冠勇等推导了承压含水层水位发生恒定下降后单层弱透水层的一维固结变形解析解[8]。Conte等推导了潜水层水位随时间波动变化时单层弱透水层中的孔压响应解析解[9]。陶立为推导了初始孔压非均匀分布时承压层水位发生恒定下降后单层弱透水层的一维固结变形解析解[10]。谢海澜等考虑土层中为非达西渗流，采用半解析法求解含水层中水位发生恒定下降后单层弱透水层的一维固结问题[11]。Tseng等考虑土层的初始重力场，通过有限差分对含水层中水位发生恒定下降后的单层土层固结问题[12]。刘加才等考虑土体为黏弹性，获得了承压层中水位降低为恒定值时的单层土层一维固结解答[13]。上述研究均针对单层弱透水的固结进行研究，水位下降形式多为瞬时下降至恒定值，与实际工程相比存在较大的偏差。

本文针对水位动态变化引发的成层地基固结问题，采用Laplace变换和传递矩阵法得出成层弱透水层固结的解析解，基于解析解对某高速铁路沿线成层弱透水层的固结性状进行了研究，计算了地下水位动态变化下成层弱透水层固结变形量、变形速率和超静孔隙水压力随时间的变化，并分析了土层压缩模量和渗透系数对土层固结变形的影响。

1 水位变化下成层弱透水层固结模型

1.1 问题描述

图1为地下水位动态变化引发成层弱透水层固结的示意，在两个承压含水层之间存在n个弱透水层，第i个弱透水层的地层厚度为bi，渗透系数为ki，体积压缩系数为mvi。初始时刻地下水位为稳定状态，在含水层中开采地下水后，地下水位发生大面积均匀下降，顶部承压含水层中的水位变化为g1(t)，底部承压含水层中的水位变化为g2(t)。

含水层中地下水位发生变化后，在弱透水层边界处产生了水力梯度，从而引发弱透水层系统发生渗流固结。

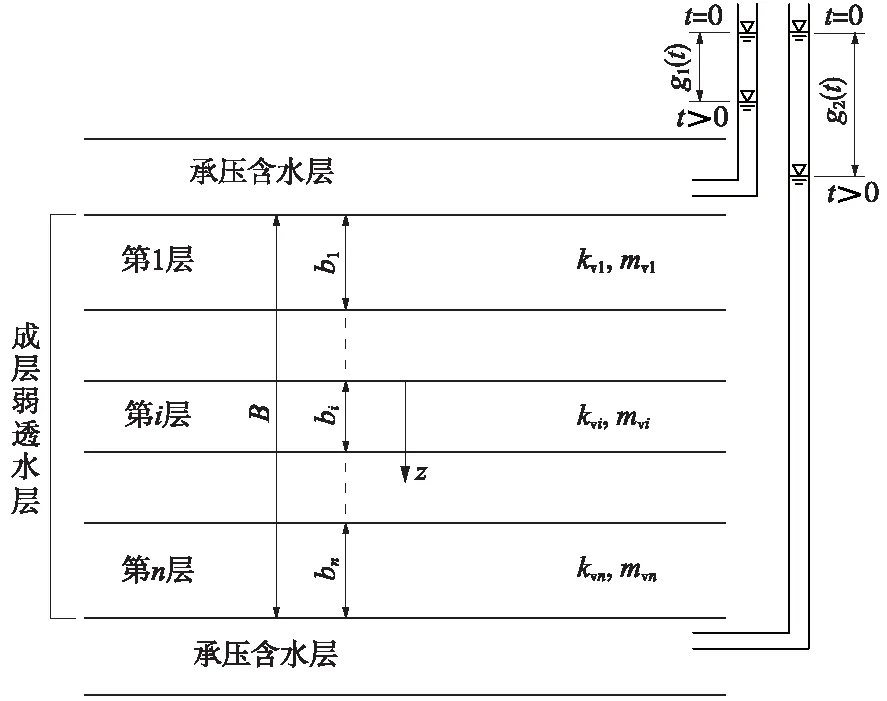
图1 水位变化引发的成层弱透水层固结示意

1.2 模型控制方程及求解条件

根据Terzaghi固结理论，成层弱透水层的固结控制方程可表示为

(1)

弱透水层间满足孔压和渗流连续条件

ui(z，t)|z=bi=ui+1(z，t)|z=0，i=1～n-1

(2a)

vi(z，t)|z=bi=vi+1(z，t)|z=0，i=1～n-1

(2b)

在初始时刻，地下水位为稳态分布，即

ui(z，t)|t=0=0，i=1～n

(3)

由于地下水位变化，在弱透水层系统顶部和底部边界处，超静孔压分别满足边界条件为

u1(z，t)|z=0=γwg1(t)

(4a)

un(z，t)|z=bn=γwg2(t)

(4b)

上述表达式(2)～式(4)为控制方程的求解条件。

2 问题模型求解

2.1 单层土固结基本解

对方程(1)进行Laplace变换后可得

(5)

求解方程(5)可得

(6)

土层竖向渗流速度为

(7)

式(6)和式(7)为单层土固结的基本解。

2.2 成层土固结解答

Bi(z，s)=Φi(z，s)·Bi(0，s)

(8)

式中,

Φi(z，s)=

由于土层间满足孔压和渗流连续条件式(2a)和式(2b)，进行Laplace变换后可得Bi(bi，s)=Bi+1(0，s)，于是根据传递矩阵法可得

Bn(bn，s)=Ψn(bn，s)·B1(0，s)

(9)

式中，Ψn(bn，s)=Φn(bn，s)·Φn-1(bn-1，s)…Φ1(b1，s)，为2×2阶矩阵。

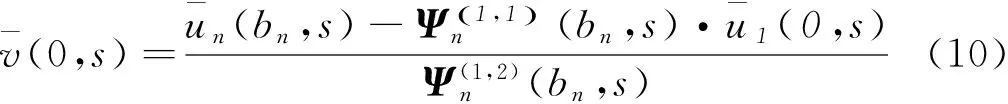
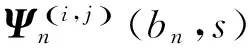
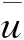
Bi(0，s)=Ψi-1(bi-1，s)·B1(0，s)

(11)

于是根据式(8)，可求得第i层土中任意位置的超静孔压和渗流速度值，进而得出第i土层的固结变形计算表达式为

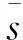
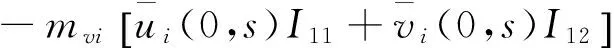
(12)

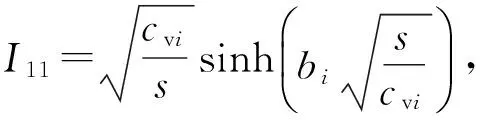
式(12)为第i土层在Laplace变换域内的解析表达式，对其进行逆变换后可得出第i土层固结沉降在时间域内的解

(13)

式中，L-1表示Laplace逆变换。

弱透水层系统总的固结变形量为

(14)

3 弱透水层固结性状分析

3.1 工程案例

图2所示为某高速铁路区段沿线典型的地层分布，在勘探范围内存在2个承压含水层，承压含水层中间包含4个弱透水层，分别为粉土层、粉质黏土层、粉土层和黏土层，各个土层的厚度、压缩模量、渗透系数如表1所示。由于沿线区域在承压含水层中开采地下水，地下水位随时间逐渐降低，根据沿线季节性用水状况，假定2个承压含水层中地下水位的变化如图3所示。

图2 某高速铁路区段沿线典型地层分布

土层编号土体类别层厚/m弹性模量/MPa渗透系数/(m/s)1粉土1.6125×10-82粉质黏土3.8155×10-93粉土6.4162×10-84黏土7.6181×10-9

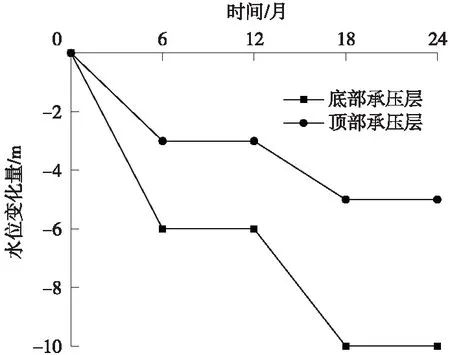
图3 含水层中地下水位动态变化

3.2 固结性状分析

根据2.2节中获得的成层弱透水层固结解析解，采用Trefethen的Laplace数值逆变换方法[14]，计算案例中成层弱透水层的固结性状。同时，采用ABAQUS有限元软件对案例工况进行模拟[15]，验证本文解析解的正确性。图4(a)为利用ABAQUS建立的有限元模型，图4(b)为解析解计算的土层总沉降量与有限元计算结果的对比。从图4(b)可以看出，解析解和有限元的计算结果完全一致，说明本文推导的解析解是正确的。随着承压层中地下水位的降低，弱透水层系统的总沉降量逐渐增加，然而弱透水层的固结沉降与地下水位的变化趋势并不完全一致，当地下水位停止降低后，弱透水层仍会继续发生固结变形，说明弱透水层系统的固结变形具有一定的滞后性，需要较长的时间才能达到稳定状态。

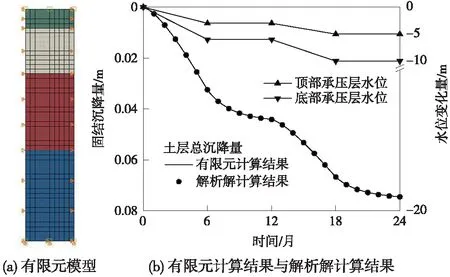
图4 解析解与有限元计算结果对比

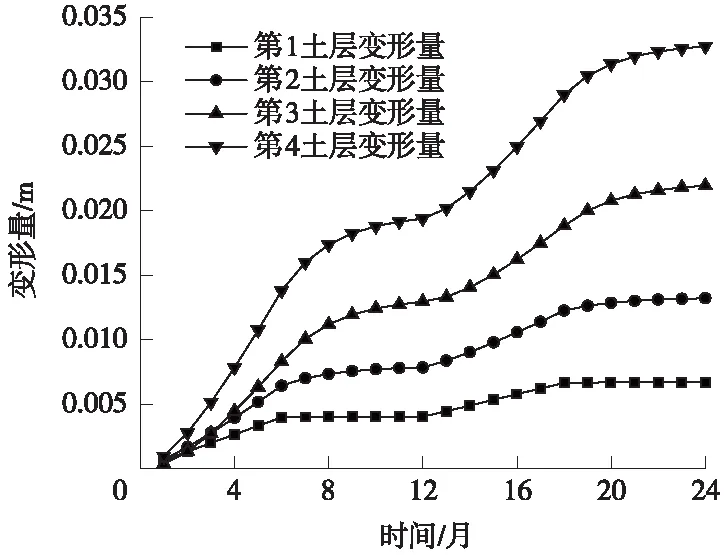
图5 各土层固结变形量随时间变化曲线

图5为各土层固结变形量随时间的变化，图6为各土层固结变形速率随时间的变化。从图5可以看出，在当前地下水位变化工况下，土层越深，变形量越大，底部第4土层的变形量最大，顶部第1土层的变形量最小。从图6可以看出，随着承压层地下水位的降低，各土层的变形速率逐渐增加，当地下水位保持恒定后，各土层变形速率逐渐减小，其中第1土层的变形速率迅速降低至0，其他土层的变形速率缓慢降低，说明第1土层很快完成固结，弱透水层系统的后续变形主要由第2、3、4土层的固结变形组成。

图6 各土层固结变形速率随时间变化曲线

图7为t=3、6、12、15、18、24月时土层中超静孔隙水压力的分布状况，图8为各土层中心处超静孔隙水压力随时间的变换。由图7和图8可以看出，随着承压层地下水位的降低，弱透水层系统中超静孔压逐渐降低，在6～12月和18～24月期间，虽然承压层地下水位保持恒定，但只有第1土层中超静孔压分布基本保持恒定，第2、第3、第4土层中的超静孔压仍有较大幅度的降低。在24个月时，第1、第2、第3土层中的超静孔压基本达到稳定状态，而第4土层中超静孔压未达到稳定状态，在30个月时才基本达到稳定状态。最终土层中超静孔压自上而下逐渐降低，其中第4土层中的孔压变化幅度最大，形成的水力梯度也最大。

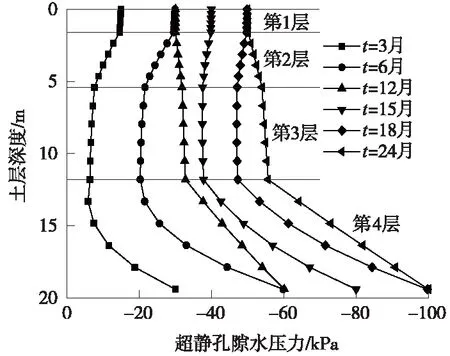
图7 超静孔隙水压力分布随时间的变化

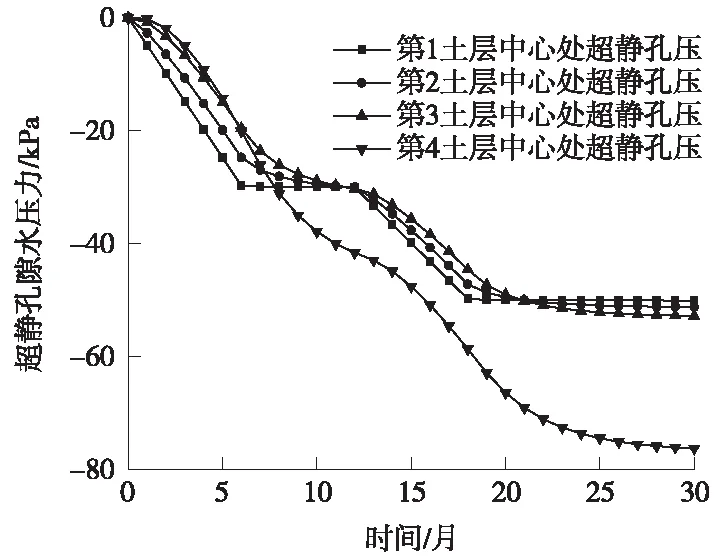
图8 土层中超静孔隙水压力随时间的变化

3.3 参数敏感性分析

从3.2节分析可知，第4土层的变形量占整个弱透水层系统固结变形量的比例最大，因此对第4土层力学参数的敏感性进行分析，包括压缩模量和渗透系数。图9为土层压缩模量对弱透水层系统固结变形的影响状况，分别计算土层压缩模量为12、15、18、21 MPa时，整个土层系统的总沉降量和沉降速率。由图9可以看出，随着压缩模量的增大，土层系统总沉降量逐渐降低，总沉降速率也逐渐降低。

图10为土层渗透系数对弱透水系统固结变形的影响状况，分别计算土层渗透系数为5×10-10m/s、1×10-9m/s、2×10-9m/s、5×10-9m/s时，整个土层系统的总沉降量和沉降速率。由图10可以看出，随着渗透系数的增加，土层系统总沉降量逐渐增加。当地下水位下降时，渗透系数越大，土层系统的变形速率越大，当地下水位保持恒定后，渗透系数越大，土层系统的变形速率越快速降低至0，说明渗透系数越大，土层系统完成固结的时间越短。

图9 土层压缩模量对固结性状的影响

图10 土层渗透系数对固结性状的影响

4 结论

(1)利用Laplace变换和传递矩阵法推导了高铁沿线地下水位动态变化引发的成层弱透水层固结解析解，通过与有限元数值计算结果对比，验证了解析解的正确性，该解答形式简单，可广泛用于高铁沿线地下水位变化引发的弱透水层固结变形计算。

(2)针对某高速铁路区段的成层弱透水层固结性状进行了计算分析，发现当地下水位逐渐降低时，土层中孔隙水压力逐渐降低，土层固结变形量和变形速率逐渐增加；当地下水位保持恒定后，土层固结变形速率逐渐降低，但土层中孔隙水压力逐渐降低，土层固结变形量逐渐增加，与水位变化相比具有较长时间的滞后性。

(3)随着土层压缩模量的增大，土层系统总沉降量逐渐降低，总沉降速率也逐渐降低。随着渗透系数的增加，土层系统总沉降量逐渐增加。当地下水位下降时，渗透系数越大，土层系统的变形速率越大，当地下水位保持恒定后，渗透系数越大，土层系统的变形速率越快速降低至0，说明土层系统完成固结的时间越短。

[1] 殷跃平，张作辰，张开军.我国地面沉降现状及防治对策研究[J].中国地质灾害与防治学报，2005，16(2):1-8.

[2] 国家铁路局.TB10621—2014 高速铁路设计规范[S].北京：中国铁道出版社，2015.

[3] 李国和，张建民，许再良，等.华北平原地面沉降对高速铁路桥梁工程的影响研究[J].岩土工程学报，2009(3):346-352.

[4] 李国和，许再良，孙树礼，等.华北平原地面沉降对高速铁路的影响及其对策[J].铁道工程学报，2007(8):7-12.

[5] 张云，薛禹群.抽水地面沉降数学模型的研究现状与展望[J].中国地质灾害与防治学报，2002(2):1-6.

[6] 田芳，罗勇，周毅，等.北京地面沉降分层监测动态变化特征[J].上海国土资源，2014，35(4):76-80.

[7] 李明霞，张云.地下水控采条件下上海土层变形特征研究[J].上海国土资源，2014(4):17-20.

[8] 骆冠勇，潘泓，曹洪，等.承压水减压引起的沉降分析[J].岩土力学，2004(S2):196-200.

[9] Conte E， Troncone A. Soil layer response to pore pressure variations at the boundary[J]. Geotechnique， 2008(1): 37-44.

[10] 陶立为.软土中水位升降引发的固结解析理论研究[D].杭州：浙江大学，2011.

[11] 谢海澜，武强，赵增敏，等.考虑非达西流的弱透水层固结计算[J].岩土力学，2007(5):1061-1065.

[12] Tseng C M， Tsai T L， Huang L H. Effects of body force on transient poroelastic consolidation due to groundwater pumping[J]. Environmental geology， 2008， 54(7): 1507-1515.

[13] 刘加才，雷国刚，梅国雄.One-dimensional consolidation of visco-elastic aquitard due to withdrawal of deep-groundwater[J]. Journal of Central South University，2012(1):282-286.

[14] Trefethen L N， Weideman J A C， Schmelzer T. Talbot quadratures and rational approximations[J]. BIT Numerical Mathematics，2006(3):653-670.

[15] 费康，张建伟.ABAQUS在岩土工程中的应用[M].北京：中国水利水电出版社，2013.