T形截面RPC简支梁抗剪性能试验及有限元分析

付 强,万冬伟,杨玉兰,金凌志

(广西岩土力学与工程重点实验室,桂林理工大学土木与建筑工程学院,广西桂林 541004)

活性粉末混凝土[1](Reactive Powder Concrete，简称RPC) 是一种具有高强度、高韧性、高耐久性和耐高温性等优越性能的水泥基复合材料，同时T形截面梁可节省材料，减轻结构自重，增大跨越能力，受力性能及抗变形性能均优于矩形梁，T形截面RPC简支梁已在实际工程中得以应用。2006年美国修建首座T形RPC单跨简支桥梁“Wapello County Mars Hill Bridge”[2]，2008年我国在蓟港铁路改造工程中第一次使用大跨度预应力活性粉末混凝土T形梁[3]，因此，研究T形截面高强钢筋RPC梁抗剪性能极具实际意义。邓宗才[4]等通过对6根T形梁的抗剪试验，探讨了压力场理论在对RPC梁抗剪分析与承载力计算时存在的问题。湖南大学陈彬[5]以T形预应力RPC梁的抗剪试验为基础，分析了不同配筋率、纵筋率、预加应力大小等对RPC梁的抗剪性能的影响。张浦[6]在软化桁架模型理论的基础上，分析了T形截面RPC梁的抗剪性能，对影响抗剪强度的配箍率、纵筋率和剪跨比等因素进行了较全面的分析。季文玉[7]通过对12根钢筋活性粉末混凝土T形梁的抗剪试验，研究了活性粉末混凝土T形梁抗剪承载力和破坏形态及主要影响因素。钟圣斌[8]等通过50根普通混凝土T形梁的试验研究表明：当翼缘宽度与梁肋宽度的比值在一定范围内时，T形截面梁抗剪承载力比矩形截面梁提高17%左右。翼缘宽度作为T形截面梁抗剪性能重要影响因素，目前关于翼缘宽度对T形截面RPC梁抗剪性能影响的研究却很少。为此本文对配置HRB500级钢筋的T形截面RPC梁进行抗剪试验，同时采用非线性有限元分析软件ANSYS对RPC试验梁进行仿真模拟，分析T形截面RPC梁的抗剪性能，研究翼缘宽度对T形截面RPC梁抗剪性能的影响。

1 试验概况

1.1 试验梁设计

本次试验共设计6根HRB500级钢筋RPC简支梁，包括3根矩形截面梁和3根T形截面梁，采用65℃高温养护3 d，常温养护28 d。梁长2 200 mm，计算跨度1 800 mm，矩形截面梁截面尺寸b×h=150 mm×250 mm，T形截面梁腹板宽150 mm，翼缘宽400 mm，梁高250 mm。RPC轴心抗压强度fc=134.6 N/mm2，受力纵筋采用φ25 mm的HRB500级高强钢筋，箍筋采用φ6 mm的HRB400级钢筋，具体试验梁参数见表1。试验梁截面尺寸及配筋见图1。

1.2 加载方式

试验梁采用三分点油压千斤顶配合反力架进行对称式加载，具体测点布置及加载方案见图2，试验现场加载见图3。

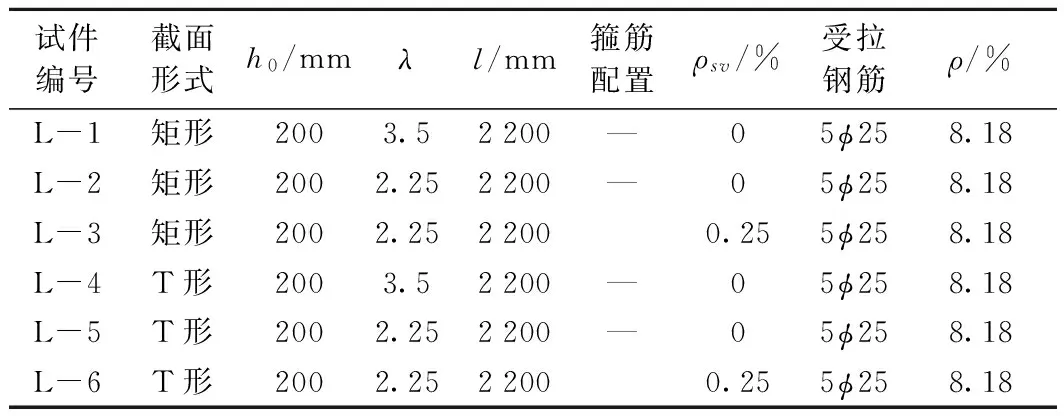
表1 试验梁参数设计

注：h0为试验梁有效高度；λ为剪跨比；l为试验梁长度；ρsv为箍筋配筋率；ρ为纵筋配筋率。

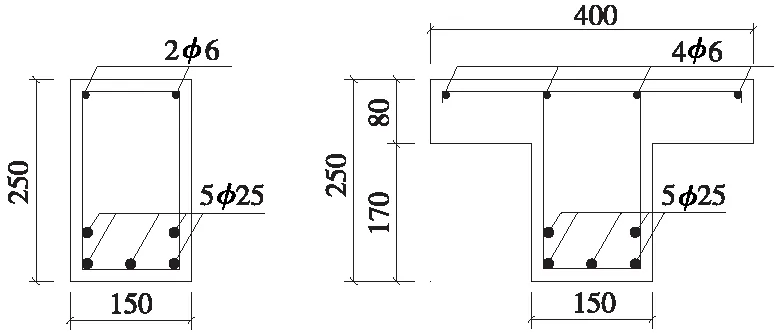
图1 试验梁截面尺寸及配筋(单位：mm)

图2 试验方案布置(单位：mm)

图3 加载试验现场

2 有限元分析

2.1 有限元模型及单元选择

钢筋混凝土带缝工作必定会使两种材料之间的变形不协调，建模时为了准确定位箍筋和纵筋，确保所建立的有限元模型与试验梁状态逼真，采用分离式模型[9]建立试验梁的有限元实体模型，将RPC和钢筋分别对应不同处理单元求解。

(1)RPC单元

混凝土属于非均匀材料，选用Solid65单元[10]能更真实地模拟混凝土材料的受力过程，包括开裂、塑性和蠕变等复杂的力学性能。

(2)钢筋单元

钢筋单元采用Link8(空间杆单元)[11]进行模拟，Link8是一种杆轴方向的拉压单元，具有塑性、膨胀、应力刚化、蠕变、大应变、大变形等效应，单元任意节点均有3个自由度(X、Y、Z方向平动)。

2.2 模型建立

2.2.1 材料本构关系

(1)混凝土材料

RPC的本构关系选用文献[12]的应力-应变关系曲线方程，在ANSYS中采用MISO模型进行模拟，相关公式见式(1)，应力-应变关系曲线见图4。

(1)

图4 应力-应变关系曲线

(2)钢筋材料

钢筋的本构模型采用BISO(双折线等强化模型)，见图5。

图5 钢筋本构模型

2.2.2 模型参数选取及建立实体模型

以试验为基础建立实际尺寸梁的分离式实体模型。混凝土单元和钢筋单元分别采用Solid65单元和Link8进行模拟，并采用约束方程的形式将两者固结在一起，忽略RPC与钢筋之间的粘结滑移。为减小钢筋与混凝土之间因耦合产生错动引起模拟结果与试验结果之间的误差，在划分模型网格时尽量使混凝土单元和钢筋单元在节点处耦合。为了更好地模拟试验梁的实际受力情况，模型的加载方式采用力加载的方式进行。为避免集中荷载引起应力集中的现象，事先切出一个加载平面，将实际的加载转化成均布荷载布置在模型上。模型采用位移收敛准则[13]，收敛精度值取0.005。模型计算关闭了混凝土的压碎检查功能，确保混凝土结构在计算中的连续性和收敛性。试验梁的ANSYS实体模型如图6所示。

图6 试验梁ANSYS实体模型

2.2.3 有限元分析结果

采用有限元软件ANSYS对RPC试验梁模型的受剪承载力进行计算分析，有限元分析结果详见表2。

表2 有限元计算分析结果

注：umax，exp为实测跨中挠度值；umax，cal为计算跨中挠度值；Vu，exp为实测抗剪极限荷载值；Vu，cal为计算抗剪极限荷载值。

图7 梁L-6纵筋应力云图

对比表2数据可知，ANSYS计算的抗剪承载力与试验实测值较为接近，但均比试验实测值略低，分析原因可能是有限元分析模型中忽略了纵筋的销栓作用和钢纤维对抗剪的作用，造成模拟值较试验值偏低。以梁L-6为例，由图7、图8、图10可知，纵筋应力的最大值分布在跨中截面或加载点附近，最小值在支座附近，箍筋应力的最大值及混凝土主应变最大值分布在支座与荷载作用点的连线的附近，与试验观测到的规律基本一致，在很大程度上能正确反映构件抗剪性能的规律，说明运用ANSYS对RPC构件进行抗剪承载力计算分析具有较好的可行性。

图8 梁L-6箍筋应力图

2.2.4 跨中挠度曲线

将有限元计算分析所得的荷载-跨中挠度曲线与试验实测的荷载-跨中挠度曲线进行对比分析，详见图9。由图9可以看出，加载过程中，有限元计算所得挠度曲线与实测挠度曲线发展较一致，其中实测挠度曲线随荷载的增加，经历的线性和非线性发展阶段更为明显，而有限元计算得到的挠度曲线非线性发展阶段并不明显，且挠度计算值小于试验实测值，即有限元模拟的试验梁延性较差。分析其原因主要是：RPC中含有钢纤维，混凝土开裂后可以继续承担一定的拉应力，但ANSYS软件分析默认当混凝土或箍筋单元在达到其指定的破坏准则后就不再受力，即退出工作；此外，实际工程中钢筋与混凝土之间存在粘结滑移，有限元计算分析模型中没有考虑两者之间的粘结滑移，也是导致挠度计算值较实测值偏小的原因之一。

图9 荷载-跨中挠度比较

2.2.5 裂缝分布及破坏形态

图10 有限元混凝土主应变分布

在本次有限元分析中裂缝的处理采用弥散裂缝模型[14]，该模型无法模拟单条裂缝的产生和发展。但是由试验现象及对试验数据的分析可知，裂缝的分布和试验梁主应变是一一对应的，通过有限元处理后的裂缝分布图中可以看到，裂缝在试验梁破坏时几乎分散于全梁，其中裂缝分布很密且主应变最大的地方即是试验中主斜裂缝经过的位置。以梁L-6为例，对试验梁破坏时有限元混凝土主应变分布(图10)、有限元混凝土裂缝分布(图11)，实测裂缝分布(图12)进行对比分析，可以看出，试验梁主斜裂缝分布的位置与有限元模拟的裂缝分布及混凝土主应变最大位置是相符的，采用弥散型裂缝虽然不能获得单条裂缝的发展规律，但是通过混凝土主应变图的变化可以获悉试验梁裂缝分布的大致位置，基本与试验结果相符。

图11 有限元混凝土裂缝分布

图12 试验梁实测裂缝分布

3 参数分析

图13为相同剪跨比和配箍率的条件下，T形截面梁和矩形截面梁抗剪承载力的对比分析图。本次试验的T形截面梁的hw/b=1.79<4属厚腹T形梁，与矩形梁在传力机理及斜裂缝的分布方面极为接近，均是由于梁顶部混凝土受到剪应力及压应力的共同作用导致破坏，但是T形梁受压区翼缘使梁顶部的剪压区面积增大，降低该处的应力值，故T形截面梁的抗剪承载力高于矩形梁，即受压翼缘的存在能使试验梁的抗剪承载力得到提高，由图13可知,T形截面梁的抗剪承载力分别较矩形截面梁提高了27.26%、21.03%、11.33%。

图13 T形梁受压翼缘对抗剪承载力的影响

文献[15]对一组腹板宽度不变，翼缘宽度不等的普通混凝土梁进行试验分析，表明当T形截面梁受压翼缘的宽度为2倍梁腹板宽度时，T形梁的承载力比矩形梁提高20%左右，再继续加宽翼缘宽度，承载力基本不再增大；研究还证明T形梁翼缘只有腹板附近的宽度能起作用，翼缘宽度超过一定值后，试件的抗剪承载力并不与受压翼缘宽度成线性增大的关系。在试验的基础上，通过有限元分析，在配箍率分别为0%和0.25%试验梁腹板厚度不变的条件下，改变翼缘宽度，取翼缘宽度分别为1、2、3、4倍的腹板宽度，分析翼缘宽度对RPC梁抗剪承载力的影响，结果如表3及图14所示。

表3 翼缘宽度对抗剪承载力的影响

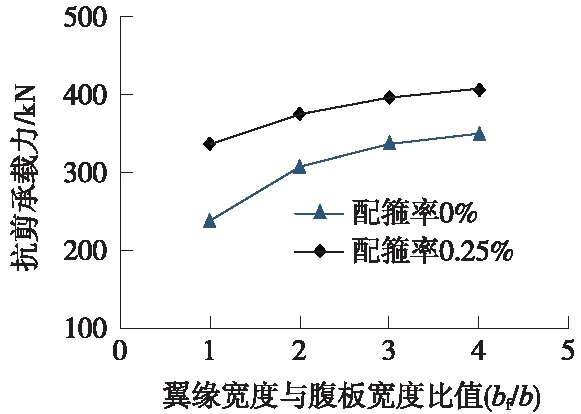
图14 翼缘宽度对抗剪承载力的影响

由表3及图14中可以看出，腹板宽度不变，翼缘宽度的增加能提高试验梁的抗剪承载力。以矩形截面试验梁的抗剪承载力为基准，当配箍率为0%，bf=2b的T形梁的抗剪承载力比矩形梁的提高为29.2%，继续加大翼缘宽度，试件的承载力基本不增大。当配箍率为0.25%，bf=2b的T形梁抗剪承载力比矩形梁的提高为11.54%，继续加大翼缘宽度，试件的抗剪承载力也基本没有变化。由此可以证明：加大翼缘宽度可以提升T形截面梁的抗剪承载力，但抗剪承载力并不随翼缘宽度的增加呈线性增长。这是因为T形梁的翼缘存在剪力滞后效应，即使继续增大翼缘宽度，也只有腹板附近的部分翼缘发挥作用。

4 结论

(1)运用非线性有限元软件ANSYS对RPC试验梁进行模拟，模拟结果基本能反映试验梁抗剪性能的规律，说明可以运用有限元对RPC试验梁的整体抗剪受力性能进行模拟分析，对工程应用具有一定适用性，但如何考虑钢纤维和纵筋的销栓作用是进一步提高模型准确度的重难点之一。

(2)通过6根RPC简支梁的抗剪性能试验研究可知，T形截面RPC梁的抗剪承载力较矩形截面RPC梁分别提高了27.26%、21.03%、11.33%，RPC试验梁采用T形截面可以提高梁的抗剪承载力及其刚度，T形截面的翼缘对限制斜裂缝宽度的作用比较明显。

(3)通过对试验现象及有限元模拟结果的共同分析，可知翼缘宽度对T形截面RPC梁抗剪性能有较大影响，当翼缘宽度与腹板宽度的比值为2时，梁的抗剪承载力提高比例最大，配箍率为0%和0.25%的T形截面RPC梁抗剪承载力较矩形截面RPC梁分别提高了29.2%和11.54%，说明翼缘宽度对T形截面RPC无腹筋梁抗剪承载力的影响更为显著。但T形翼缘存在剪力滞后效应，其宽度超过一定值后对试验梁抗剪承载力的影响逐渐减弱。

[1] 金凌志，温晴.活性粉末混凝土梁斜裂缝宽度影响参数探析[J].铁道标准设计，2016，60(7)：94-98.

[2] Thorsten Stengel, Peter Schiebl. Life cycle assessment of UHPC bridge constructions: SHERBROOKE footbridge, KASSEL GARTNERPLATZ footbridge and WAPELLO road Bridge[J]. Architecture civil engineering environment, 2009(1):109-118.

[3] 艾丹.活性粉末混凝土简支T梁试制与探索[J].中国建材科技，2014，23(2)：171-174.

[4] 邓忠才，周冬至，程舒锴.配筋活性粉末混凝土梁抗剪承载力[J].哈尔滨工程大学学报，2014，35(12)：1512-1518.

[5] 陈彬.预应力RPC梁抗剪性能研究[D].长沙：湖南大学，2007.

[6] 张浦.基于软化桁架理论的RPC梁斜截面抗剪承载力研究[D].北京：北京交通大学，2011.

[7] 季文玉，丁波，安明喆.活性粉末混凝土T形梁抗剪试验研究[J].中国铁道科学，2011，32(5)：38-42.

[8] 钟圣斌，程翔云.关于钢筋混凝土T形截面梁的抗剪强度[J].重庆交通学院学报，1991(4)：34-43.

[9] 张陶方.钢筋混凝土薄壁箱梁抗剪性能研究[D].长沙：湖南大学，2009.

[10] 司炳君，孙治国，艾庆华.Solid65单元在混凝土结构有限元分析中的应用[J].工业建筑，2007，37(1)：87-92.

[11] 田双珠，丁嵬，王元战.基于ANSYS的钢筋混凝土构件裂缝宽度计算方法[J].水工港口，2008，29(5)：351-357.

[12] 北京交通大学.活性粉末混凝土铁路预制梁的设计与试验研究报告[R].北京：北京交通大学，2007.

[13] 江见鲸.钢筋混凝土结构非线性有限元分析[M].西安：陕西科学技术出版社，1994.

[14] 郝文化.ANSYS土木工程应用实例[M].北京：中国水利水电出版社，2005.

[15] 过镇海，时旭东.钢筋混凝土原理[M].北京：清华大学出版社，2003.