Marshall-Olkin Fréchet分布应用于产品抽样检测

赵春雪，李树有，宓 颖

Marshall-Olkin Fréchet分布应用于产品抽样检测

赵春雪，李树有，宓 颖

（辽宁工业大学 理学院，辽宁 锦州 121001）

研究了Marshall-Olkin Fréchet分布在产品抽样检测上的应用。如何对寿命服从Marshall-Olkin Fréchet分布的产品进行质量检验，从消费者的角度，给出了在大批量抽取和小批量抽取2种情况下，试验所需的最小样本容量。在此基础上，考虑生产者所承担的风险，从而得到满足要求的产品的最小平均寿命值。

Marshall-Olkin Fréchet分布；抽样检测；最小样本容量；平均寿命真实值

Frechét分布是一种特殊情况下的广义极值分布，也被称作逆威布尔分布[1]，能够广泛应用于确定产品寿命、维修时间、强度等可靠性工程中。2000年，Kotz等[2]对Frechét分布进行了详细的介绍，其分布函数为：

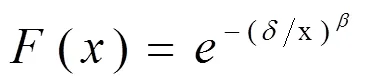
生存函数为：

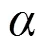
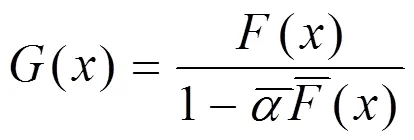
即：

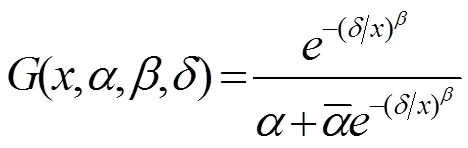
在产品的质量检测中产品的生产材料、生产步骤、使用方式、使用环境等是影响产品质量的因素，需要对大量的产品进行抽样试验，来决定消费者和生产者是否接受这批产品。Kantam等[5]和Srinivasa Rao等[6]讨论了log-logistic模型与Marshall-Olkin扩展指数分布的验收抽样方法。2013年，Krishna等[7]对Marshall-Olkin Fréchet分布的性质进行了介绍并给出了相关证明。本文主要介绍了Marshall-Olkin Fréchet分布在产品抽样检测上的应用。本文中，考虑产品的寿命决定产品的质量，且在抽样试验中，采用不重复抽样的方式。

1 试验所需最小样本容量

当产品寿命服从Marshall-Olkin Fréchet分布时，对产品进行截尾寿命试验。“”为试验开始前确定的时间，单位h。如果产品在前失效的个数不超过，那么称为合格，并且希望产品合格时接受的概率至少为。如果产品在前失效的个数超过，则试验终止，拒绝这批产品。基于此，考虑利用最小的样本容量得到相关决策。由于产品寿命服从Marshall-Olkin Fréchet分布，由式(2)可得当和已知时，平均寿命时间取决于，令0为所需要的最小平均寿命时间，()(，，，)随着的增加减少，从而得到：

即抽样计划制定由以下4点决定：试验所用的样本容量，所能接受的数量，试验进行的最大持续时间，最小平均寿命时间0。

从消费者的角度考虑产品失效时接受的概率应该不超过1-，其中由、、0/确定。若试验为大批量抽取[8]，为批量，/≤0.05时，那么接受这批产品的概率应用二项分布计算，利用下式：

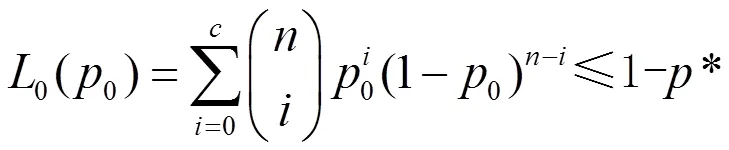
其中0(，，，0)。

若试验为小批量抽取，即0(，，，0)小而样本容量相对较大，此时二项分布接近参数为=0的泊松分布，则上式转换为：

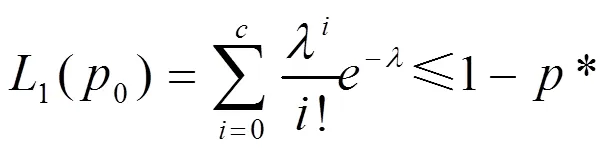
考虑来自文献[4]文章中的数据，0分别取值0.562、0.762、0.953、1.212。表1和表2分别讨论了为0.75、0.90、0.95、0.99，2、2时，应用二项分布和泊松分布，试验所需的最小样本容量。

结论：由表1和表2可得消费者对产品的质量要求越高，即越大，试验所需的样本容量越大。若对产品质量检测的批量没有要求，试验采取大批量抽取所需的样本容量较小，从而减少浪费。

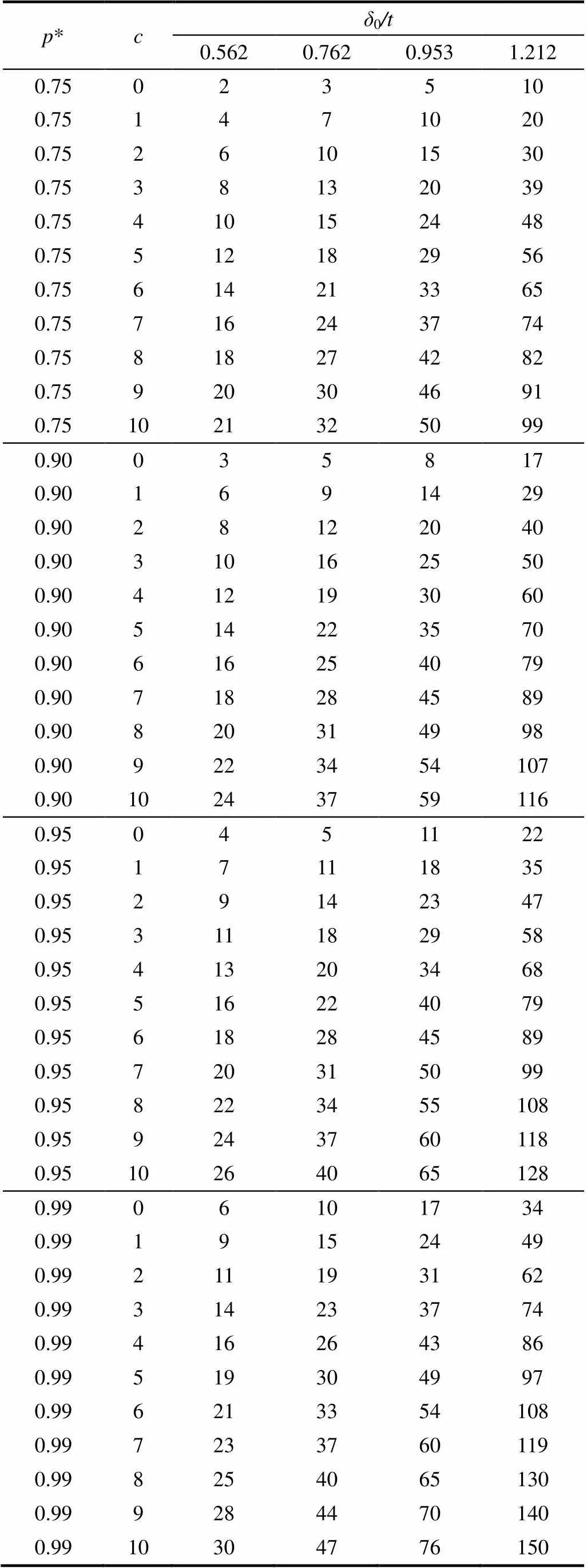
表1 应用二项分布

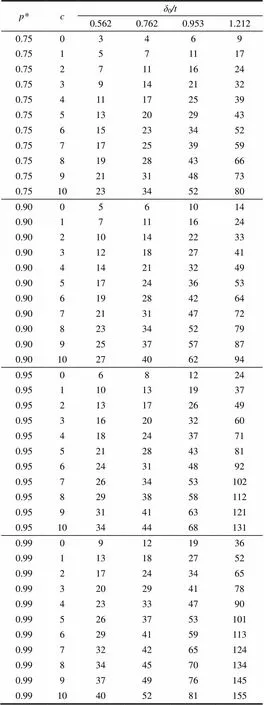
表2 应用泊松分布

2 确定最小平均寿命时间

根据消费者的接受程度，得到了抽样的最小样本容量。在此基础上，从生产者的角度考虑，是否接受这批产品。生产者接受这批产品的概率用二项分布来计算：

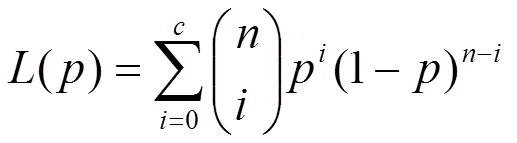
这里的(，，，)，为平均寿命的真值。则生产者是否接受这批产品的概率取决于与消费者角度所需的最小平均寿命0的比值，表3给出了当/0分别取1.5、2.0、2.5、3.0、3.5时，生产者接受这批产品的概率。

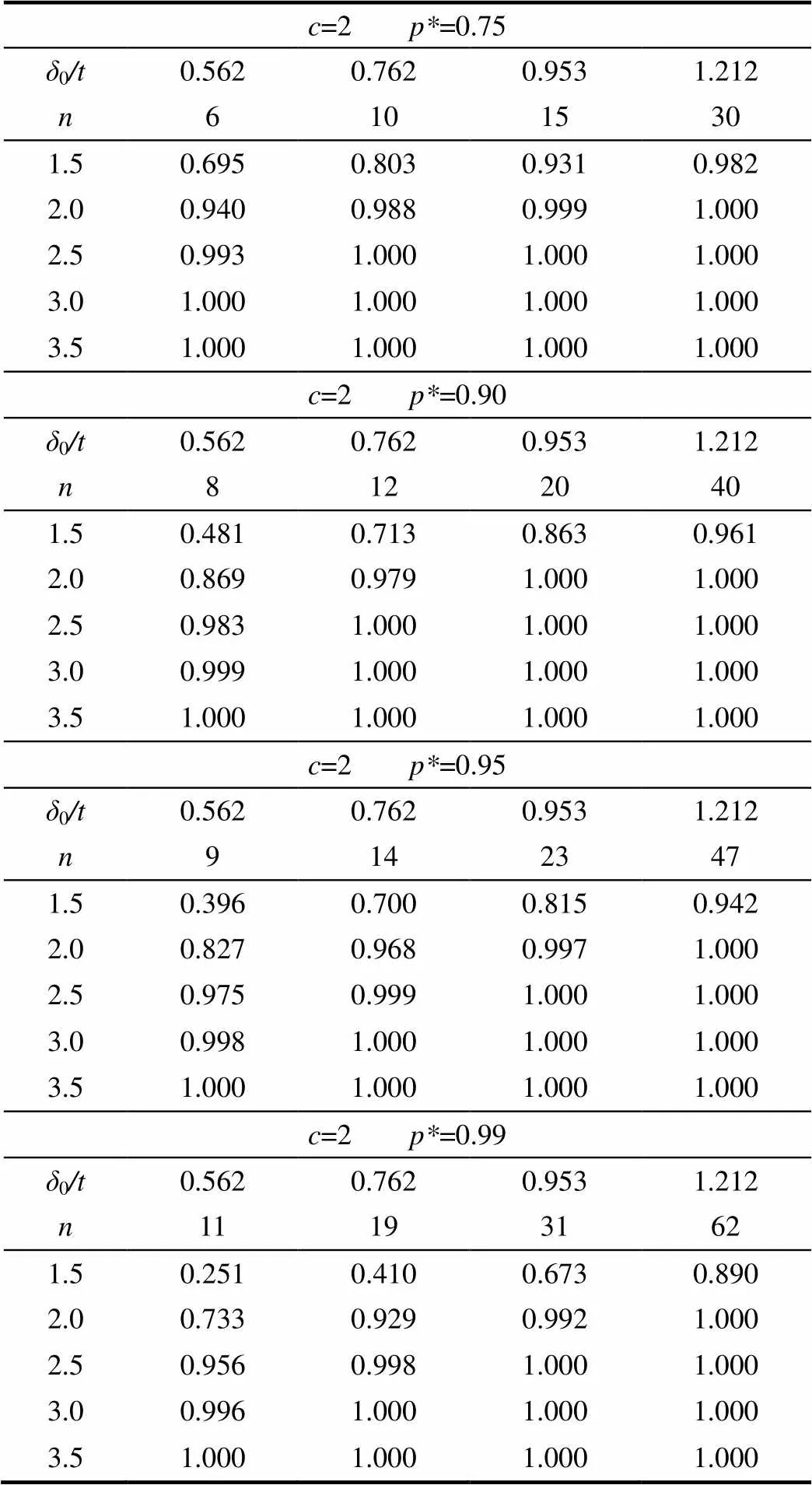
表3 接受产品的概率

结论：置信水平取值0.90时，满足要求的抽样计划为（=8，=2，00.562），得到/0为1.5、2.0、2.5、3.0、3.5时，生产者接受的概率分别为0.487、0.869、0.983、0.999、1.000。表明，如果产品真实平均寿命是给定平均寿命0的2倍，生产者所承担风险概率为0.131，当产品真实的平均寿命是给定平均寿命0的3.5倍以上时，生产者所承担风险接近0。而当取值逐渐增加，消费者要求提高时，生产者接受这批产品的概率降低。

一般情况下，假定生产者承担风险的概率不超过0.05。为确保生产者承担风险的概率不超过0.05，考虑比值/0满足：

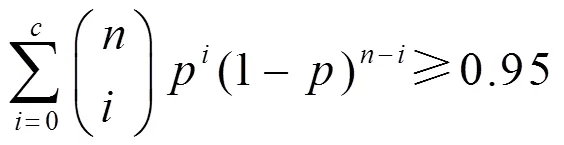
根据表3中给定的置信水平得到的抽样计划（，，0），可以计算出满足式(7)/0的最小比值，见表4。

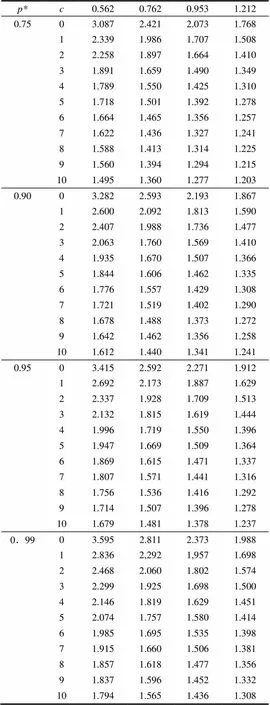
表4 δ/δ0最小比值

结论：当和0/取不同值时，为了满足生产者的需求，可以得到/0的最小比值。根据表4，=2，=0.95，0/=0.562时，0=2.337也就是产品的真实平均寿命时间应该是给定平均寿命时间的2.337倍，此时才能满足生产者所承担风险的概率不超过0.05的要求。若=1 000 h，0=562 h，从消费者和生产者两方综合考虑，产品的平均寿命时间最小为1 336 h。

[1] 韩庆田, 卢洪义, 杨兴根. 逆威布尔分布模型及其应用[J]. 质量与可靠性, 2006, 124(4): 18-21.

[2] Kotz S, Nadarajah S. Extreme Value Distributions[J]. Theory and Applications, 2000, 83(3): 744-752.

[3] Marshall A W, Olkin I. A new methods for adding a parameter to a family of distribution with application to the exponential and weibull families[J]. Biometrica, 1997, 84(4): 641-652.

[4] Krishna E, Jose K K, Alice T, et al. Applications of Marshall-OlkinFréchet distribution[J]. Communications in Statistics Simulation and Computation, 2013, 42(1): 76-89.

[5] Kantam R R L, Rosaiah K, Srinivasa Rao G. Acceptance sampling based on life tests: log-logistic model[J]. Journal of Applied Statistics, 2001, 28(1): 121-128.

[6] Srinivasa Rao G, Ghitany M E, Kantam R R L. Reliability test plan for Marshall-Olkin extended exponential distribution[J]. Applied Mathematical Sciences, 2009, 3(55): 2745-2755.

[7] Krishna E, Jose K K, Alice T, et al. Marshall-Olkin Fréchet distribution[J]. Communications in Statistics Theory and Methods, 2013, 42(1): 76-89.

[8] 王敏华. 大批量计数抽样方案的制定[J]. 浙江工程学院学报, 1999, 16(2): 123-127.

责任编校：孙 林

Application of Marshall-Olkin Fréchet Distribution to Product Sampling Inspection

ZHAO Chun-xue, LI Shu-you, MI Ying

（College of Science, Liaoning University of Technology, Jinzhou 121001, China）

The application of Marshall-Olkin Fréchet distribution to product sampling inspection is introduced in this paper. As to how to inspect the product quality that the life time of the product follows Marshall-Olkin Fréchetdistribution, the minimum sample size in the two cases of large volume extraction and small batch extraction is considered from the consumer’s point of view,. On this basis, the risk borne by producer is taken into account, so as to get the minimum value of the average life of the product.

Marshall-Olkin Fréchet distribution; sampling inspection; minimum sample size; average life

10.15916/j.issn1674-3261.2017.06.001

O212

A

1674-3261(2017)06-0351-04

2017-06-06

赵春雪(1993-)，女，河北保定人，硕士生。 李树有(1964-)，男，辽宁锦州人，教授，博士。