城市垃圾填埋场不均匀沉降的研究

周爱鹏，孙洪军，边旭阳



城市垃圾填埋场不均匀沉降的研究

周爱鹏，孙洪军，边旭阳

（辽宁工业大学 土木建筑工程学院，辽宁 锦州 121001）

针对城市垃圾填埋场垃圾堆填压缩和降解所引起的不均匀沉降问题。本文通过阅读大量的国内外研究文献，综合了各个沉降模型的发展，给出了发展中的不足与解决方法。并提出利用FLAC 3D计算机数值模拟对垃圾场沉降进行计算，该软件可以得到清楚的沉降云图，结论接近实际工程，利用该软件分析填埋场不均匀沉降，对填埋场库容量的估算提供准确的依据。

城市垃圾填埋场；不均匀沉降；FLAC 3D；数值模拟

据有关资料表明，全世界垃圾产量约为1.5×108t，平均年增长速度为8.42%，虽然我国处于发展中国家，目前大中型城市的固体废物的日产量已达15亿kg，人均1.5 kg，而且我国垃圾增长率达到10%以上[1-2]，如此大产量势必要采用大量的人力物力处理。然而在处理城市固体废物(MSW)垃圾，目前采用主要方法有卫生填埋法、焚烧发电法、堆填法等。卫生填埋就是由环卫部门将城市垃圾专门集中到填埋场，进行机械压实后以每层2.5～3.0 m厚度进行填埋，在达到设计高度后进行封场[3]。卫生填埋法简单易行、投资较少、具有处理各个种类的固体垃圾的好处。缺点是占用大量的土地且垃圾降解的速率不稳定与时间长。焚烧法虽然在短时间内可以获得热能用于发电，但会极大程度上污染环境，不符合绿色可持续的经济发展。堆填法采用微生物对有机物成分降解，使之成为堆肥。其成本较高，且处理后利用效率也不高，对我国目前的经济发展状况还不太适合。所以目前我国较合适的垃圾处理方法是分层卫生填埋法。

对于垃圾体卫生填埋处理最棘手的问题就是不均匀沉降。造成这种现象的因素主要为填埋体在各点埋深随着山体变化(例如山谷型)、垃圾各部分的比例和城市发展有关[4]。垃圾体的来源有很多，主要由废弃的建筑材料和日常厨余菜品组成。两者分别影响土体的高程和自重从而影响上层堆填土体对下层土体的附加应力，垃圾成分的不一决定了有机物含量，从而影响有机质降解的速率[5]。

1 国内外城市垃圾填埋场沉降研究现状

纵观研究城市垃圾场沉降的文献有很多，绝大部分学者关心沉降特点和机理，提出了各式各样的计算模型和假设，仅有少部分的学者去细微地观察和研究垃圾填埋场沉降的不均匀性特点。在计算机数值模拟出现之前，对于沉降的不均匀性研究要靠对城市垃圾填埋场埋设多个观测点进行沉降测量，所耗的精力相当大，所以目前关于这方面的理论和结论还不是很多。但大量的室内的沉降模拟实验和现场试验总结出多种沉降模型的计算方法和垃圾土的土性参数为将来计算机数值模拟提供了对比的保障。接下来是关于国内和国外关于填埋体沉降机理的研究。

1.1 国内城市垃圾填埋场沉降研究现状

1996年，同济大学朱青山等[4]分别用聚乙烯桶装载人工配制的垃圾、居民生活垃圾进行试验分析，初步拟合出降解沉降随时间变化的线性关系，以及证明了N、P和K的加入可以促进垃圾降解，缩短稳化时间。

2000年，浙江大学温振统[5]通过国外现有的填埋场实测沉降数据与国内填埋场内可降解有机物实测结果进行对比，给出了填埋场内有机物的分解规律公式：

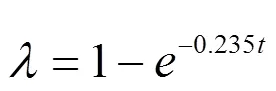
2001年，浙江工业大学胡敏云等[7-8]认为沉降由主(自重的沉降)、次沉降(垃圾蠕变调整)、有机物降解，其中主、次沉降都是以孔隙比减小引起的。并给出了计算主压缩常用的主、次压缩指数公式：

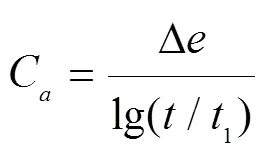
式中：0为压实后的初始孔隙比。

2000年，同济大学黄仁华等[9]通过对上海老港填埋场进行面积为3 000 m2的填埋沉降试验，在2.5年的试验观测中发现最大沉降值超过初始填埋高度的25%。并对上海老港填埋场沉降变形规律进行了研究，认为降解所引起的沉降与时间呈对数线性关系。根据数学模拟结果推算封场25年后的沉降值。

2002年同济大学黄仁华等[9]、刘鹰疆等[10]认为沉降分3个阶段：初始阶段、第一阶段、第二阶段。初始阶段的沉降发生在填埋中瞬时沉降；第一阶段的沉降主要是由于垃圾空隙中的水分和气体被上层垃圾土压实而散逸引起的，大约持续1～6个月；第二阶段的沉降主要来自垃圾降解。

2004年，重庆大学罗锋等[11]用3种垃圾填埋场单元模拟器对废物降解试验对比分析，得到生物反应器填埋场具有快速降解的作用，给到了pH=7.2、温度控制在40～41℃、水分含量65%左右时最佳。

2006年，大连理工大学孔宪京等[12]归总对国内外填埋场沉降的研究方法，并介绍了各种沉降模型以及它们的参数使用条件。同年，谢焰等[13]提出考虑气固耦合填埋场一维沉降计算模型。他们[14]在研究垃圾压缩机理的基础上同时考虑降解和分级堆填的填埋场沉降计算方法，并对模型参数进行了研究。修正了Gibson和Lo流变模型中认为主压缩、最终降解压缩应变随应力呈线性增加的不合理性假定。

2007年，杨治贵等[15]对深圳下坪垃圾填埋场进行降解沉降测量，由于在填埋2年后进行的6个月的测试，所得的沉降数据为6.13 cm远小于根据2006年河海大学陈继东等[16]等提出的垃圾土沉降模型所计算出有机物降解所引起的沉降4.4 m。

2009年，浙江大学柯瀚等[17]完善并改进了生物降解模型，该模型既可以解释常压力下的试样压缩，也可以分析分层堆填填埋场的容量分析和对封场后沉降预测。分析了苏州七子山填埋场填埋体重度和孔隙比随填埋深度的计算拟合曲线。

2010年，浙江大学徐晓兵等[18]通过上海老港填埋场填埋期间埋设的水平沉降管监测，得到了从2006—2008年不同埋深的沉降数据。给出了填埋体的压缩应变约为0.197～0.242，填埋场垃圾在3个月内基本完成主压缩固结，修正次压缩参数为0.066～0.070。

2011年，同济大学席永慧等[19]利用计算机模拟软件FLAC 3D，通过现场和室内压缩实验得到各层堆体土性参数，对上海老港垃圾填埋场垃圾土坝的稳定性进行分析。发现FLAC 3D在沉降稳定性方面较传统方法更直观、方便、全面，可得到位移、应力分布图。

2011年，河海大学方荣等[20]用FLAC 3D软件模拟苏州七子山填埋场老场封场后的沉降，并在此基础上以4 m一层堆载的方式在老场上建立新场，得到了老场的“二次不均匀沉降”的云图。结果显示，最大沉降发生在老场中间部位，最大沉降量约为老场封场后堆体厚度的20%左右。

2014年，中国钢研科技集团邱光习[21]通过CAD、EXCEL、SURFER以及FLAC 3D内置的FISH语言对城市垃圾填埋场进行三维分层建模。

2016年，辽宁工业大学范艳超[22]建立了长50 m、宽50 m，高20 m城市垃圾填埋场的模型进行沉降计算，发现场地地基中央最大的沉降为4.91 m，与采用建筑地基设计规范的计算值相差不大。

1.2 国外城市垃圾填埋场沉降研究现状

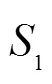
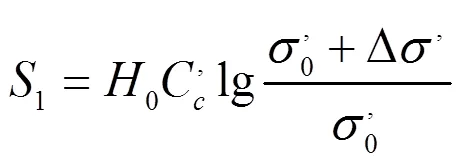
1975年，Yen等[24]对3个填埋场沉降数据的研究，提出估算垃圾沉降的对数模型，因为沉降的快慢与时间的对数呈线性关系：

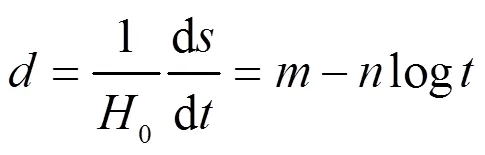
1990年Edil等[25]认为主、次压缩的界定模糊，想建立以任意时间为基准接下来的沉降计算单一公式。他认为垃圾填埋体的沉降机理与有机土、泥炭类似。因此，采用预测泥炭、有机土沉降的幂函数公式，引入填埋体沉降的模型幂函数公式：

1990年，Edil[25]等修改Gibson等提出的描述土体长期压缩变形特征的流变模型：

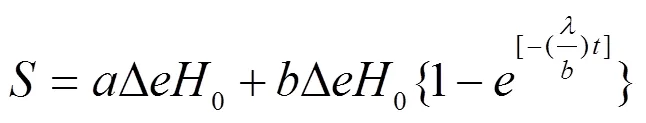
1990年后许多室内模拟试验和填埋场实测沉降结果表露，填埋体在经历一段次沉降后有一段明显按时间对数增长，Bjarngard等[26]提出长期修正次沉降公式：

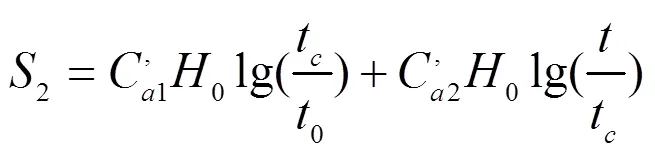
1992年，Edgers等[27]提出生物引起的沉降模型，其表达式：

式中：0为生物降解开始的时间存在争议；、为参数。

Park等[28-29]分别于1997年和2002年提出次沉降中由降解引起的公式：

2003年，有些学者认为，次沉降在经历一段时期时有加速现象，归结为生物降解带来的，因此将次压沉降归结为蠕变和生物降解2部分。对于蠕变引起的沉降，一些学者仍用Sower所提出的次压缩与时间的对数公式，Afonso等[30]认为流变模型较为合适。

2003年，Marques等[31]提出了应力、蠕变、降解3者作用的综合模型。模型计算公式如下：

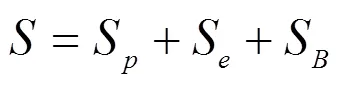
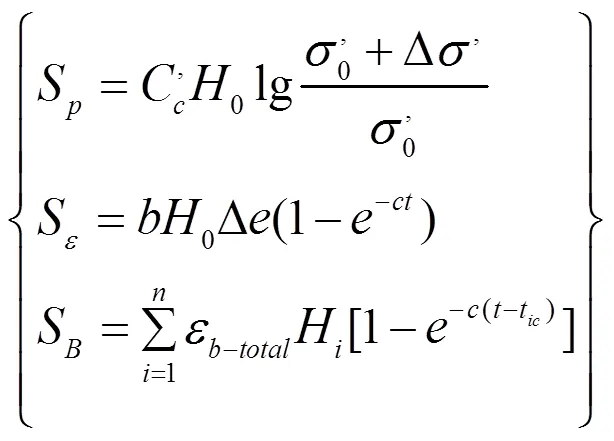
式中：3者分别用Sower模型、Gibson流变模型、Park生物降解模型计算沉降量。

对国内外各种实验理论可以得出大概2个思路，在研究城市垃圾体沉降是不是要考虑分别主、次沉降。因为最早开始研究填埋体沉降Sower初次引入主、次沉降的概念，所以直到现在大部分学者一直沿用。Sower模型给出的沉降与应力对数、时间有关被人所接受。接下来说明有关主、次沉降理论的发展，主固结为垃圾体的短暂的瞬时沉降也被大家认可。然而对于次固结研究比较多：主、次固结的压缩系数取值；次固结是不是可以多条曲线模拟；次固结沉降曲线用了多种曲线模拟如对数函数、幂函数等；次固结与主固结时间界限合理的取值。

(1)对于主、次压缩系数，国内胡云敏、张振营等对其做了充分的探索与结论。

(2)对于次沉降曲线因为后期的加速现象解释，学者们给出了分段函数的次固结曲线。

(3)从修正的对数函数（两段次固结参数不同对数函数）→前半段蠕变的对数函数、后半段降解的幂函数（生物降解模型）→两段幂函数（流变函数+生物降解模型）。这样就解释了Sower模型→流变模型→生物降解模型→综合模型的发展。

（4）对于次固结与主固结时间界限合理的取值至今任然在探索之中，给出的时间大致为1个月、3～6个月、5年等都得不到广泛的认可。

除了对次固结的研究，他们根据现场测得的沉降曲线提出了单一的主、次固结合并的模拟曲线，著名的有对数模型、幂函数模型、双曲线模型等。

2 国内外计算沉降研究存在的问题

虽然在研究城市垃圾填埋体沉降方面取的了一些进展，下面给出几点不足。

(1)对于现阶段沉降模型还不能广泛地利用，这是因为各个填埋场的差别太大，不管从填埋场的规格和垃圾体的有机物含量等影响了沉降，在这种情况下模型函数的参数存在着较大差异。

(2)垃圾土独特堆填方式影响主、次固结的时间界限取值。这是因为垃圾土随时间增加的高程并不是呈线性的关系，这对分层取值有一定的差异。现有的模型越来越注重分层计算沉降。

(3)随着各种物理、化学、生物的措施，填埋场的沉降曲线与现代城市填埋场的拟合已经发生了转变(如分层分类填埋、渗滤液回灌技术、生物反应器填埋场等)。

(4)国内填埋场沉降量相对于国外同样高度的垃圾填埋场沉降量较大。在国外沉降模型的基础上，找到合适的沉降机理和特点还有一段路要走。

3 结论与展望

(1)为了建立一个合理沉降模型还需大量现场沉降数据的拟合，研究模型参数时给出对应合理的解释。对比各个城市填埋场用同一个模型，比对参数变化情况，给出各种关系对参数的影响。

(2)对于当前模型只考虑自重应力这1个条件而忽略填埋过程，考虑城市垃圾填埋场加权平均填埋速率值和绘制填埋高程与时间的曲线得到时间的中心值，推理时间的中心值和次固结开始时间关系。

(3)对比现代填埋场沉降值与现有模型在相同高程下的结果，逐步修正模型和其参数。

(4)近年来，由于FLAC 3D计算机数值模拟软件以其模拟得到的结论与实际工程状况对比相差不大，不但可以得到清楚沉降云图和各单元网格节点沉降数据，在分析各高程表面的不均匀沉降起到了关键的作用，故利用该软件分析填埋场不均匀沉降可以成为发展趋势。

[1] 王志萍. 城市固体废弃物的压缩特性及填埋场沉降分析[D]. 杭州: 浙江工业大学, 2007.

[2] 王薇, 完颜华, 王驰. 兰州市城市生活垃圾处理研究[J]. 环境科学与管理，2007, 32(5): 126-129.

[3] 刘骏龙. 城市固体废弃物的压缩试验及其填埋场沉降模型研究[D]. 杭州: 浙江大学, 2010.

[4] 朱青山, 赵由才, 徐迪民. 垃圾填埋场中垃圾降解与稳定化模拟试验[J]. 同济大学学报, 1996, 24(5): 596-600.

[5] 温振统. 城市固体废气物填埋场沉降与稳定分析[D]. 杭州: 浙江大学, 2000.

[6] 张振营, 吴世明, 陈云敏. 城市生活垃圾土性参数的室内试验研究[J]. 岩土工程学报, 2000, 22(1): 35-39.

[7] 胡敏云, 陈云敏. 城市生活垃圾填埋场沉降分析与计算[J]. 土木工程学报，2001, 34(6): 88-92.

[8] 胡敏云, 陈云敏, 温振统. 城市垃圾填埋场垃圾土压缩变形的研究[J]. 岩土工程学报, 2001, 23(1): 123-126.

[9] 黄仁华, 赵由才, 周海燕. 大型垃圾填埋场表面沉降研究[J]. 上海环境科学, 2000, 19(8): 399-401.

[10] 刘疆鹰, 徐迪民, 赵由才, 等. 城市垃圾填埋场的沉降研究[J]. 土壤与环境, 2002, 11(2): 111-115.

[11] 罗锋, 陈万志, 李小鹏, 等. 三种垃圾填埋场单元模拟器对废物降解的对比试验[J]. 中国环境科学, 2004, 24(4): 474-479.

[12] 孔宪京, 孙秀丽. 城市固体废弃物沉降模型研究现状及其进展[J]. 大连理工大学学报, 2006, 46(4): 615-622.

[13] 谢焰, 陈云敏, 唐晓武, 等. 考虑气固耦合填埋场沉降数学模型[J]. 岩石力学与工程学报, 2006, 25(3): 601-608.

[14] 谢焰, 陈云敏, 柯瀚. 考虑降解和分级堆填的填埋场一维沉降计算[J]. 水文地质工程地质, 2008(1): 102-105.

[15] 杨治贵, 胡亚东. 垃圾填埋体沉降计算方法[J]. 有色冶金设计与研究, 2007, 28(4): 95-98.

[16] 陈继东, 施建勇, 方云飞. 垃圾土降解规律及填埋场沉降计算分析研究[J]. 河海大学学报, 2006, 34(6): 680-682.

[17] 柯瀚, 陈云敏, 谢焰, 等. 适宜降解条件下填埋场的沉降模型及其案例分析[J]. 岩土工程学报, 2009: 31(6): 929-938.

[18] 徐晓兵, 詹良通, 陈云敏, 等. 城市生活垃圾填埋场沉降监测与分析[J]. 岩土力学, 2010, 22(1): 35-39.

[19] 席永慧, 熊浩. 老港填埋场的稳定性三维数值模拟分析[J]. 结构工程师，2011, 27(5): 78-84.

[20] 方荣, 靳永福, 丰土根. 受扩建工程影响的老垃圾填埋场沉降分析[J]. 人民长江, 2011, 42(10): 36-38.

[21] 邱光习. 垃圾填埋场FLAC 3D建模方法研究[J]. 山西建筑, 2014, 40(14): 287-289.

[22] 范艳超. 基于单元分层法对城市垃圾填埋场沉降的研究[D]. 锦州: 辽宁工业大学, 2016.

[23] Sower G F. Settlement of waste disposal fills[A]. Proceeding of the 8th international conference on soil mechanics and Foundation Engineering[C]. Moscow: [s.n], 1973: 207-210.

[24] Yen B C, Scanlon B. Sanitary landfill settlement rates[J]. Journal of Geotechnical Engineering, ASCE, 1975, 101(5): 475-487.

[25] Edil T B, Ranguette V J, Wuellner W W. Settlement of municipal refuse[M]//Geotechnics of waste fills theory and practices. Philadephia: Landva and Knowles, Eds, 1990: 225-239.

[26] Bjarngard A, Edgers L. Settlement of municipal solid waste landfills[C]//Proc 13thAnnual Madison waste conf. Wis: University of Wisconsin, Madison, 1990: 192-205.

[27] Edgersl, Noble J J. A biological model for long term settlement in landfills[M]//Environmental Geotechnology Rotterdam: A. A. Balkem a, 1992: 177-184.

[28] Park H I, Lee S R. Long-term settlement behavior of landfills with refuse decomposition[J]. Journal of Solid Waste Technology and Management, 1997, 24(4): 159-165.

[29] Park H I, Lee S R, Dony. Evaluation of decomposition effect on long-term settlement prediction for fresh municipal solid waste[J]. Geotech Geoenviron Eng, 2002, 128(2): 107-118.

[30] Afonso Celso Moruzzi Marques, George M Filz, Orencio Monje Vilar. Composite compressibility model for municipal solid waste[J]. Journal of Geotechnical and Geoenviromental Engineering, 2003, 129(4): 373-379.

[31] Marques A C M, George M F, Wilar O M. Composite compressibility model for municipalsolid waste[J]. J of Geotech and Geoenviron Eng, 2003, 129(4): 372-378.

责任编校：孙 林

Research on Uneven Settlement of Urban Landfill

ZHOU Ai-peng, SUN Hong-jun, BIAN Xu-yang

（School of Civil and Architectural Engineering, Liaoning University of Technology, Jinzhou 121001, China）

In view of the problem of uneven settlement due to the compression and degradation of municipal landfill waste, the shortcomings and solutions in development are presented in this paper according to a large number of domestic and foreign research documents as well as the development of various subsidence models. Then the simulation calculation of landfill settlement value is put forward to get clear images of settlement by using the FLAC 3D. The conclusion is close to the actual engineering field, so that analysis of uneven settlement of landfill by using this software provides the basis for accurate estimation of landfill storage capacity.

municipal landfill; uneven settlement; FLAC 3D; the numerical simulation

10.15916/j.issn1674-3261.2017.06.015

R730.58

A

1674-3261(2017)06-0408-05

2017-06-19

国家自然科学基金青年基金项目(51408290)

周爱鹏(1993-)，男，江苏盐城人，硕士生。 孙洪军(1973-)，男，辽宁彰武人，教授，博士