核运动对H2+谐波辐射的影响

冯立强

核运动对H2+谐波辐射的影响

冯立强

（辽宁工业大学 理学院，辽宁 锦州 121001）

理论研究了H2+在电子与核耦合的非伯恩奥本海默近似下辐射高次谐波的特点。结果表明，由于核运动的影响，奇次谐波辐射呈现红移现象。但是随着振动态增大，谐波红移现象逐渐减弱；谐波光谱呈现非奇次谐波。并且随着振动态增大，非奇次谐波明显增强。通过研究谐波辐射时频分析图以及谐波辐射随核间距离变化的演化图，给出了H2+谐波辐射红移以及非奇次谐波产生的原因。

高次谐波；核运动；谐波红移；非奇次谐波

高次谐波作为一种非常有效的探测原子、分子动力学的方法被广泛研究[1-3]。目前，利用半经典三步模型可以有效地解释高次谐波的辐射过程[4]，即：(i)电子首先由隧道电离或多光子电离进入连续态；(ii)进入连续态的电子在激光场驱动下以经典方式运动；(iii)在激光场反向驱动时，电子向原子核运动并与其发生回碰辐射高次谐波。

分子相比于原子具有更为复杂的结构，因此当其与强激光场相互作用后，会产生一些分子特有的现象。例如：Lein[5]发现分子谐波辐射强度与其振动自相关函数有关。Zhang等[6]和Feng等[7]理论研究了分子谐波辐射的空间分布。Bian等[8]研究表明，激光诱导电子跃迁在分子谐波辐射中起很大的作用。Bian等[9]研究表明，谐波辐射在激光上升以及下降区间分别呈现红移和蓝移现象。Feng等[10]发现较轻的核辐射谐波强度要高于较重的核。

虽然，近年来对分子谐波辐射过程的研究取得了很多进展[5-10]，但是多数模型都采用电子与核分离的伯恩奥本海默近似模型，因此关于核运动对分子谐波辐射的影响却少有报道。因此，鉴于上述原因，本文理论研究了H2+在电子与核耦合的非伯恩奥本海默近似下辐射高次谐波的特点。

1 理论模型

激光场和H2+相互作用可以通过求解电子与核耦合的非伯恩奥本海默近似薛定谔方程来描述[11]：

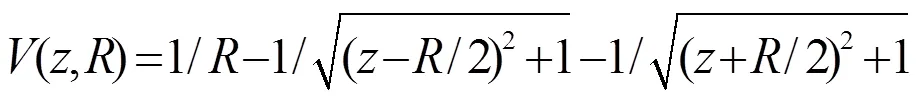
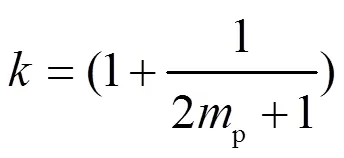
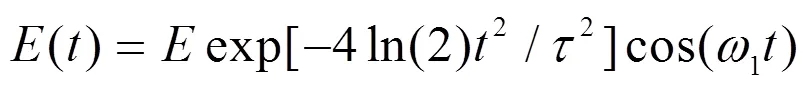
这里，p、、分别为H核质量、核与电子坐标。1、、和分别为激光场的频率、振幅和脉宽。

高次谐波谱图可以表示为：

其中：

2 结果与讨论

图1给出H2+不同振动态在6.8 fs-800 nm，= 3.0×1014W/cm2(表示激光场光强)的激光场驱动下辐射谐波的特点。一般来说，在核固定模型下，由于激光场的对称性，谐波光谱只呈现规则的奇次谐波。但随着考虑核运动的影响，谐波光谱呈现2个明显的特点，即：(i)奇次谐波呈现红移；(ii)谐波光谱呈现非奇次谐波。随着振动态增大，谐波红移现象逐渐减弱，但非奇次谐波明显增强。

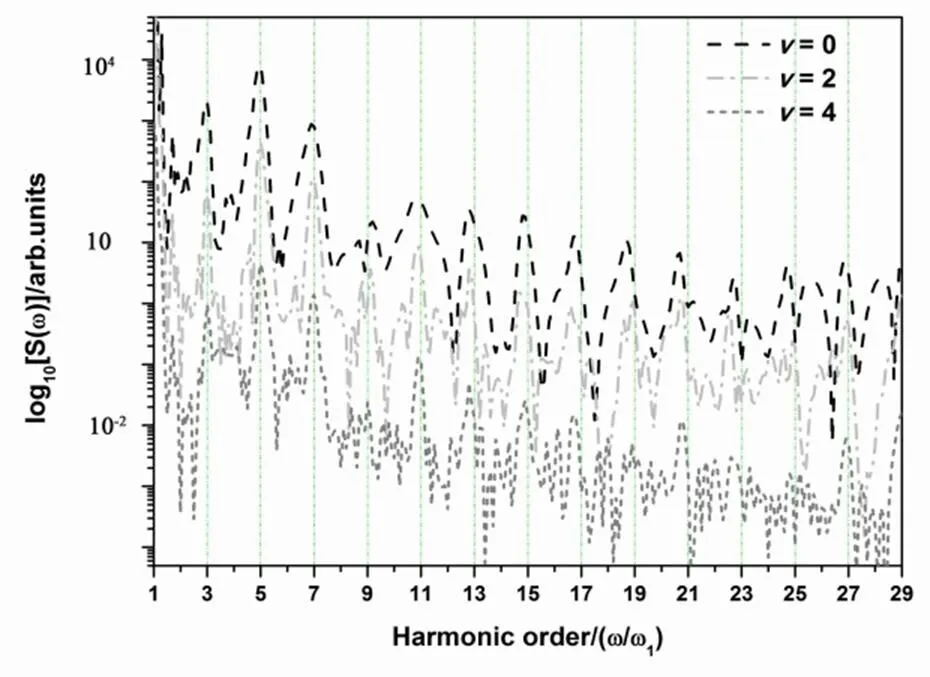
图1 H2+谐波辐射谱图

由三步模型可知，在激光场的上升区间[d()/d> 0]，由于激光强度的持续增强，后电离的电子会获得更多的能量，进而导致谐波光谱的蓝移；相反在激光场的下降区间[d()/d< 0]，由于激光强度的持续减小，后电离的电子将获得较低的能量，进而导致谐波光谱的红移。分析谐波辐射的时频分析图[12]，如图2所示可知，在本文所用激光场下，可以呈现许多个谐波辐射过程。对于振动基态(= 0)，由于激光强度在上升区间较弱，H2+在激光上升区间不能被充分电离，因此导致其谐波辐射在激光上升区间(< 2，其中代表激光场光学周期)的强度要远小于激光下降区间(> 5)，即，谐波辐射强度主要来源于激光下降区间，如图2(b)所示，因此导致谐波光谱的红移。随着振动态增大，H2+在激光上升区间的谐波辐射强度增强，如图2(c) [= 2]和图2(d) [= 4]所示，因此导致谐波光谱红移减弱。

(a)激光包络图 (b) v = 0 (c) v = 2 (d) v = 4

图3给出了H2+核间距随时间的变化以及谐波辐射随核间距的变化。由图3可知，当= 0时，最大核间距离出现在5.5 a.u.处；当= 4时，最大核间距出现在7.0 a.u.处。由此可见，随着振动态增大，核间距离被明显延伸。并且，从图中可观测到，当< 5.0 a.u.时，只有奇次谐波可以观测到。但是当> 5.0 a.u.时，谐波辐射出现频移并且还会出现一些非奇次谐波。并且由于核间距离的增大，高振动激发态出现非奇次谐波的强度被明显增强。由此可见，非奇次谐波出现的原因是由于核运动引起的分子对称性遭到破坏所导致的。

(a) H2+核间距随时间的变化 (b) v =0 (c) v =4

3 结论

理论研究了H2+在非伯恩奥本海默近似下谐波辐射的特点。结果表明，(1)在核运动的影响下，奇次谐波呈现红移现象。但是随着振动态增大，谐波红移现象逐渐减弱。(2)谐波光谱呈现非奇次谐波。并且随着振动态增大，非奇次谐波明显增强。理论分析表明谐波频移是由于谐波辐射在激光上升和下降区间的不对称性所导致的。非奇次谐波产生的原因是由于核运动引起的分子对称性遭到破坏所导致的。

[1] Krausz F, Ivanov M. Attosecond physics[J]. Rev Mod Phys, 2009, 81(1): 163-234.

[2] Feng L Q, Chu T S. Generation of an isolated sub-40-as pulse using two-color laser pulses: Combined chirp effects[J]. Phys Rev A, 2011, 84(5): 053853.

[3] Feng L Q.Molecular harmonic extension and enhancement from H2+ions in the presence of spatially inhomogeneous fields[J]. Phys Rev A, 2015, 92(5): 053832 .

[4] Corkum P B. Plasma perspective on strong field multiphoton ionization[J]. Phys Rev Lett, 1993, 71(13): 1994-1997.

[5] Lein M. Attosecond probing of vibrational dynamics with high-harmonic generation[J]. Phys Rev Lett, 2005, 94(5): 053004.

[6] Zhang J, Pan X F, Xia C L, et al. Asymmetric spatial distribution in the high-order harmonic generation of a H2+molecule controlled by the combination of a mid-infrared laser pulse and a terahertz field[J]. Laser Phys Lett, 2016, 13(7): 075302.

[7] Feng L Q, Li W L. Nuclear signature effect on spatial distribution of molecular harmonic in the presence of spatial inhomogeneous field[J]. Laser Phys, 2017,27(1): 016002.

[8] Bian X B, Bandrauk A D. Multichannel molecular high-order harmonic generation from asymmetric diatomic molecules[J]. Phys Rev Lett, 2010, 105(9): 093903.

[9] Bian X B, Bandrauk A D. Probing nuclear motion by frequency modulation of molecular high-order harmonic generation[J]. Phys Rev Lett, 2014, 113(19): 193901.

[10] Feng L Q, Chu T S. Nuclear signatures on the molecular harmonic emission and the attosecond pulse generation[J]. J Chem Phys, 2012, 136(5): 054102.

[11] Lu R F, Zhang P Y, Han K L. Attosecond-resolution quantum dynamics calculations for atoms and molecules in strong laser fields[J]. Phys Rev E, 2008, 77(6): 066701.

[12] Antoine P, Piraux B, Maquet A. Time profile of harmonics generated by a single atom in a strong electromagnetic field[J]. Phys Rev A, 1995, 51(3): R1750-R1753.

责任编校：孙 林

Effect of Nuclear Motion on High-order Harmonic Generation from H2+

FENG Li-qiang

（College of Science, Liaoning University of Technology, Jinzhou 121001, China）

Electron ()-nuclear () dynamics in molecular high-order harmonic generation (MHHG) from H2+has been theoretically investigated with the Non-Bohn-Oppenheimer approximation. The results show that due to the effect of the nuclear motion, the red-shifts of the odd harmonics can be found. However, with the increase of the initial vibrational state, the red-shifts of the harmonics are decreased. The non-odd harmonics can be obtained on the harmonic spectra. Moreover, as the initial vibrational state increases, the generations of the non-odd harmonics are enhanced. Throughstudying the time-frequency analyses of the harmonics and thedependence of the MHHG, the reasons behind the red-shifts of the harmonics and the generations of the non-odd harmonics are given.

high-order harmonic generation; nuclear dynamics; red-shifts of the harmonics; non-odd harmonics

10.15916/j.issn1674-3261.2017.06.002

O562.4

A

1674-3261(2017)06-0355-03

2017-08-31

冯立强(1985-)，男，辽宁沈阳人，副教授，博士。