链式多边形与三角形的稳定性的理想模型
☉湖北省武汉科学技术馆 张忠斌
一直以来,在数学词典中都找不到三角形的稳定性的确切定义,现有各种版本的教材中给出的描述性定义也不统一,同时,给出的实验模型也比较粗糙.本文拟提出链式多边形,并以此构建一种有关三角形的稳定性的理想模型,或可对认识这一问题有所帮助.
一、教材中三角形的稳定性描述
三角形的稳定性一直是初中几何的一个教学内容.它早期出现在上海人民出版社1973年版《几何》[1].内容如下:
我们先来做一个实验:用木条钉一个三角形和一个四边形的架子,如果拉动这两个架子,就会发现三角形架子的形状始终不变,而四边形架子的形状可以改变.这个事实说明,三角形具有一种使结构不变的性质,我们把这种性质叫做三角形的稳定性.由于三角形具有稳定性,采用三角形结构,就能增加物体的坚固程度,而且又节约了材料,因此它在生产实践中被广泛地采用.
由吉林工业大学数学教研室编的1973年版《几何》[2],对三角形的稳定性的表述如下:
由定理3,我们知道一个三角形如果三边固定下来,那么这个三角形的形状就随之固定下来了,就是说,外力不改变三角形的形状,这就是所谓的三角形的稳定性.
笔者读初中所用的几何课本是人教版1981年版《几何》[3].有关三角形的稳定性的内容与上述表述相当,只是多画了两幅示意图.内容如下:
边边边公理表明,只要三角形三边的长度固定,这个三角形的形状和大小就完全确定.例如,取三条长度适当的木条,用钉子把它们钉成一个三角形,所得到的三角形的形状和大小就固定(图1).三角形这个性质叫做三角形的稳定性.这是三角形特有的性质.其他多边形就没有这种特性.例如,把四条长度适当的木条订成一个四边形的架子,它的形状是可以改变的(图2).
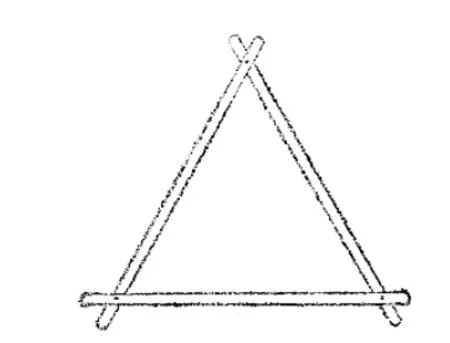
图1
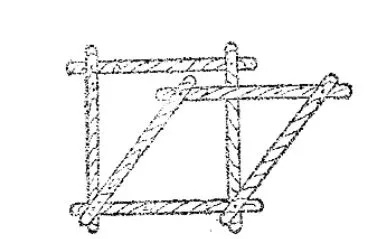
图2
最新版本的人教版2013年版八年级《数学》[4]也有关于三角形的稳定性知识点.该书没有给出三角形的稳定性定义,但却得出了如下的一些提问和结论:
如图3(1),将三根木条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗?
如图3(2),将四根木条用钉子钉成一个四边形木架,然后扭动它,它的形状会改变吗?
如图3(3),在四边形木架上在钉一根木条,将它的一对不相邻的顶点连接起来,然后扭动它,这时木架的形状会改变吗?为什么?
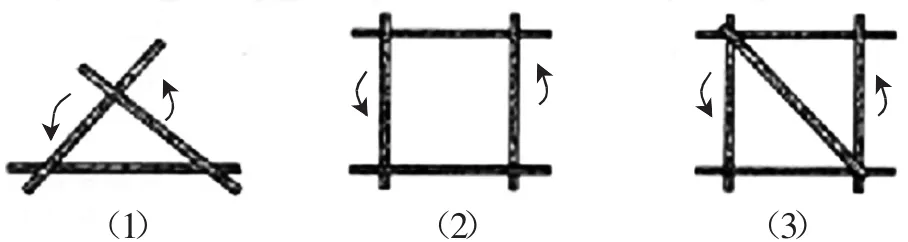
图3
可以发现,三角形木架的形状不会改变,而四边形木架的形状会改变.这就是说,三角形是具有稳定性的图形,而四边形没有稳定性.
上述“用木条钉一个三角形和一个四边形的架子”,这个验证三角形的稳定性的实验模型显得很粗糙;一是钉子与木条是否都垂直,二是钉子与木条之间必定有很大的摩擦力,三是木条与木条之间也有一定的摩擦力.这三个因素都会阻碍木条的旋转,于是就造成了操作时需要“拉动”,从而看起来像力学实验一样,容易造成几何与力学的理解上的混乱.这个不良模型需要改进.
二、链式多边形及三角形的稳定性的理想模型
为了讨论三角形的稳定性,有必要引入旋转点和链式多边形概念.关于旋转点,可以从角的动态定义和圆的一个定义中找到.一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形叫做角.所旋转射线的端点叫做角的顶点.当一条线段绕着它的一个端点在平面内旋转一周时,它的另一个端点的轨迹叫做圆.
借此可以定义旋转点.空间上具有旋转特性的点,叫做旋转点.采用同心圆“ ”表示,内圆表示旋转点,外圆表示旋转;或者借用圆心符号“⊙”来表示,内中的点表示旋转点,外圆表示旋转.上述角的顶点和圆心都是旋转点.以下分别用“ ”和“⊙”表示角的顶点和角.如图4所示.

图4
这个图形看起来像钟表的两个指针,可以绕轴旋转.也就是,顶点为旋转点的角,其角度不是固定不变的.
由端点为旋转点的线段组成的多边形叫做链式多边形.那么,在所有的链式多边形中,只有三角形的形状是不变的.下面用旋转点组成链式三角形和链式四边形,旋转点用“⊙”表示.如图5所示.
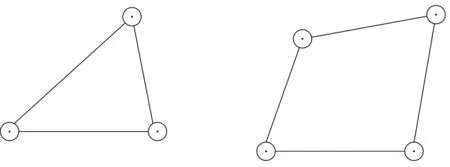
图5
比较图4中的角和图5中的链式三角形,可以看出,如果让顶点为旋转点的角固定不变,可以连接这个角的两条边组成一个三角形,那么这个角就不会再改变了.实际中,将人字梯的两个支撑梯的横档用一根绳子的两端分别系住,展开绷紧,人字梯就稳固了;一些圆规的设计也采用了这种原理.
下面笔者结合链式多边形提出较为理想的实验模型.
三角形的稳定性的实验模型:在光滑合适的木条两端分别钻直径相等的孔,在木条与木条之间配上减少摩擦力的垫圈,再用相当尺寸的销子适当锁定,组成链式三角形和链式四边形.如图6所示.
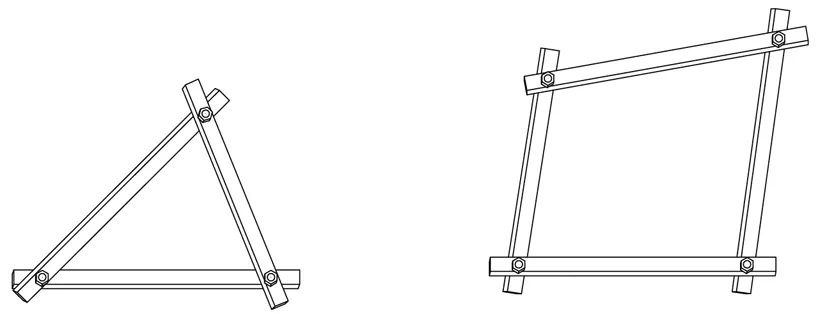
图6
这里钻的孔和销子所组成的结构就相当于旋转点的结构.轻轻拨动这两个木架,会发现三角形木架的形状始终不变,而四边形木架的形状可以改变.也就是说,在链式多边形中,只有链式三角形的形状固定不变.链式三角形的这种性质叫做三角形的稳定性.
如果将链式四边形的一条对角线连接起来,组成两个链式三角形,这样的图形其形状也固定不变.这一点体现在理想实验模型上,则是用木条代替对角线,钻孔锁定.如图7所示.

图7
三、结束语
三角形的稳定性同三角形的确定性[5]“给定三边,则三角形唯一确定”命题有所联系.另外,三角形的稳定性也可以同余弦定理相联系:已知三角形的三边,根据余弦定理可以计算出三角形三个角的度数.也就是说,给出三角形的三条边,那么这个三角形的三个角都可以计算出来,相当于这三个角也都给出了,从而链式三角形的形状固定不变.
三角形的稳定性问题主要是特殊图形的形状是否存在不变性的问题,这类特殊图形可称之为链式多边形.本文得到的结论是:在链式多边形中,只有链式三角形的形状固定不变而具有稳定性.
1.《初等数学》编写组.《几何》[M].上海人民出版社,1973.
2.吉林工业大学数学教研室编.《几何》[M].吉林工业大学,1973.
3.中小学数学编辑室编.《几何》(第一册)[M].人民教育出版社,1981.
4.课程教材研究所等编著.《数学》(八年级上册)[M].人民教育出版社,2013.
5.张忠斌.三角形的确定性问题探究[J].中学数学(初中版),2017(5).

