基于“数学好玩”，领悟数学思想

胡俊平

摘 要：“基本思想”是2011版《数学课程标准》提出的“四基”目标之一。新北师大版小学数学教材中的“数学好玩”栏目是让学生对基本数学思想进行领悟的有效载体，在“数学好玩”栏目教学中，要善于引导学生在操作探究的过程中展开相应的数学学习活动，让他们领悟基本数学思想。

关键词：“数学好玩”；数学思想；领悟

2011版《数学课程标准》提出了“四基”目标，把“基本思想”确立为“四基”之一。可见，在数学教学中对学生进行基本数学思想的渗透教育是十分重要的，这样，才能让学生在这个过程中领悟基本数学思想，从而促进他们数学素养的提升。在新北师大版小学数学教材中，设置了“数学好玩”栏目，这一栏目的教学是让学生对基本数学思想进行领悟的有效载体，在“数学好玩”栏目教学中，要善于引导学生在操作探究的过程中展开相应的数学学习活动，从而在这个过程中让他们领悟基本数学思想。

一、引导数学操作，领悟分类思想

《数学课程标准》特别强调“做数学”，“做数学”是小学生开展数学学习的一种重要形式，而动手操作则是小学生“做数学”的有效载体。在“数学好玩”栏目中有一些内容涉及了数学分类思想，教学中，教师要善于引导学生在动手操作的过程中对数学分类思想进行领悟。

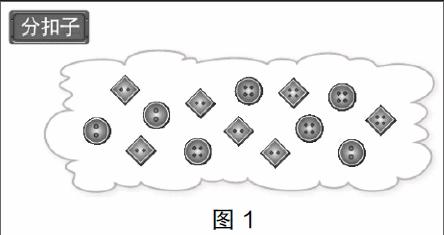
【案例】 “分扣子”教学片段（新北师大版小学数学一年级下册）

出示情境图：

师：小朋友们，请你们仔细观察这些扣子的特点，如果让你们分一分，你准备怎么分？

生：我觉得可以按照扣子的形状分一分。

生：也可以按照扣子眼数的不同分一分。

师：现在请你拿出一号学具袋中的扣子分一分。在分的过程中要思考有几种不同的分法？第一次分了以后还能继续分吗？最后分得的结果一样吗？

（学生动手操作分扣子。）

师：刚才小朋友们都已经分好扣子了。谁愿意到黑板上来把你分扣子的方法分给其他同学看？

生：我把圆形的扣子放在一起，把方形的扣子放在一起。

师：小朋友們，仔细看！他把扣子分成两类。那么，他是根据什么分的呢？

生：他是按照扣子的形状不同分的。

师（板书：形状）：还能继续分下去吗？（追问上台分的同学）

生：还可以。把2个扣眼的放在一起，把4个扣眼的放在一起。（边说边分）

师：他在继续分的过程中是按照什么分的呢？

生：是根据扣眼的不同来分的。

师：同学们。刚才这一位小朋友把这一些扣子分成4类。他是先按照什么分？再按照什么分的？谁能完整地说一说他分的过程？

生：他是先按照形状分，再按照扣眼数分，把这些扣子分成4类的。

师：你把他分的过程说得真完整。谁还有不同的分法？

（另一位学生准备上台分。）

师：这位小朋友在分的时候你们一定要仔细观察。并且在观察的过程中要思考他是先按照什么分，再按照什么分，最后把扣子分成几类。

生：他是先按照扣眼数分，再按照形状分，把扣子分成4类。

师：小朋友们，你们刚才分扣子有两种方法？这两种分法有什么相同点和不同点吗？

生：相同点是都是分两次。

生：都是按照“形状”和“扣眼数”这两个标准分的。分后的结果是一样的。

师：那不同点呢？

生：第一种分法是先按照形状分，再按照扣眼数分；而第二种分法是先按照扣眼数分，再按照形状分。

分类思想的核心是分类标准。如果对一年级的小学生进行分类标准的说教，他们肯定是不明白的。以上案例中，教师让学生动手操作经历分扣子的过程，并且引导他们对两种不同的分扣子方法进行比较，这样，在这个过程中学生就对“分类标准”进行了有效感悟，从而在这个过程中体验到了分类数学思想。

二、引导数学探究，领悟有序思想

有序思想是思考问题的一种有效方法，同时，也是一种重要的数学思想。小学生掌握有序思想对于他们的数学学习具有十分重要的作用，对于他们今后解决问题同样具有重要的作用。在“数学好玩”栏目中，有一些内容蕴含着有序思想的因子，教学中，教师要引导学生在数学探究的过程中对有序思想进行领悟。

【案例】“数图形的学问”教学片段（新北师大版小学数学四年级上册）

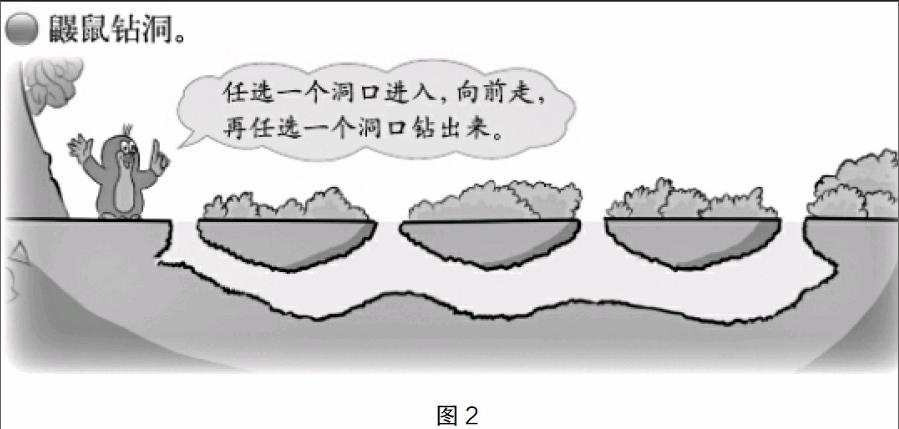
师：鼹鼠是一种很喜欢钻洞的动物，请看大屏幕（课件）。

师：如果鼹鼠（出示句子）任选一个洞口进入，向前走，再任选一个洞口钻出。

师：这句话中你认为哪个词很重要？为什么重要？你能举个例子说说吗？

生：如：B进只能从C或D出来。

生：任意，追问：什么意思？请举个例子说一说，如可以从A、B、C、D进入，C进不能C出。

师：那猜猜看这样走到底有几条路呢？

生：4条。

生：5条。

生：6条。

师：像这样讲得清楚吗？那你有什么办法让别人能看明白。

生：老师，我觉得可以用画线段图的方法。

师：你准备怎么画？如果说不出来，我们可以请线段图来帮忙。

出示（课件）这里的A、B、C、D表示的是4个洞，问题：那一共有多少条不同的路线？

要求：（1）请你在线段图上画一画，鼹鼠钻洞的不同路线

（2）在画的时候，怎样才能做到不重复不遗漏。

（3）用算式表示路线的总条数。

师：老师看了下，大部分同学都已经完成，现在请这位同学来展示。问：你是怎么有序画线段图的？（把过程画在黑板上）

师：当学生画完3条后，问：等等老师这儿还有红色的粉笔，你是想继续用白色的粉笔还是用红色的，让别人能看得更清楚？（2条）再一条。endprint

师：你刚才用了三种不同的颜色表示出来了所有的路线，那你的算式是：3+2+1（板书）。

追问：3表示什么意思？2表示什么意思？1表示什么？从A、B、C洞出发的，跟他一样的请举手，不一样的呢？

学生反馈刚才他用了三种颜色去画，你需要吗？说一说算式里的1、2、3分别是什么意思？

师：刚才我们借助线段图解决了鼹鼠钻洞的路线问题，看来线段图是我们进行数学学习的好帮手。我们用线段图帮助解决这类数学问题的时候要注意什么？（板书：有序）有序其实就是我们做到——不遗漏，不重复。

师：其实线段图可以解决生活中的很多数学问题，如老师从东阳坐车去上海（从东阳站出发，途经义乌、杭州、南京到上海站）在买票的时候，车站的工作人员就碰到了这样的一个问题（出示课件：单程票需要准备多少种不同的车票？）

问：单程是什么意思？能举个例子吗？（青田到船寮，青田到海口……）

问：只能从青田出发吗？你能不能结合这个问题画出线段图？并用算式表示数的过程。

反馈：（投影展示）。

问：你是怎么画的？你的算式是4+3+2+1=10， 这里的4、3、2、1分别表示什么？

追问：还有不一样的画法吗？（板书：5个站 4+3+2+1）

师：刚才我们解决了5个车站的车票问题，如果有6个车站呢？（出示：单程需要准备多少种不同的车票？）

（板书：6个站5+4+3+2+1）

师：鼹鼠钻洞的路线，线段上有4个点，有3+2+1=6条；5个车站有多少种单程票，线段上有5个点，有4+3+2+1=10种；6个站有几种单程票，线段上有6个点，有5+4+3+2+1=15种，那如果是7个站呢？（板书7个站）那8个站呢？（板书8个站）你发现了什么规律？

以上案例中，正是因为教师基于具体的问题情境引导学生经历数学抽象的过程，把实际的数学问题抽象成线段图，然后，基于线段图这一学习素材进行数路线的探究，学生在数学探究的过程中，经历了有序思考的过程，掌握了有序思考的方法，收到了很好的教学效果。

三、引导数学实验，领悟化归思想

所谓化归思想就是将一个问题由难化易，由繁化简的思想过程。化归思想是一种重要的数学思想方法，并且是一种解决问题的高效方法。在“数学好玩”栏目中，根据实际问题设计了一些数学实验，小学生在開展这一些数学实验的过程中，就要经历化繁为简的过程，在这个过程中能够有效地对化归思想进行领悟。

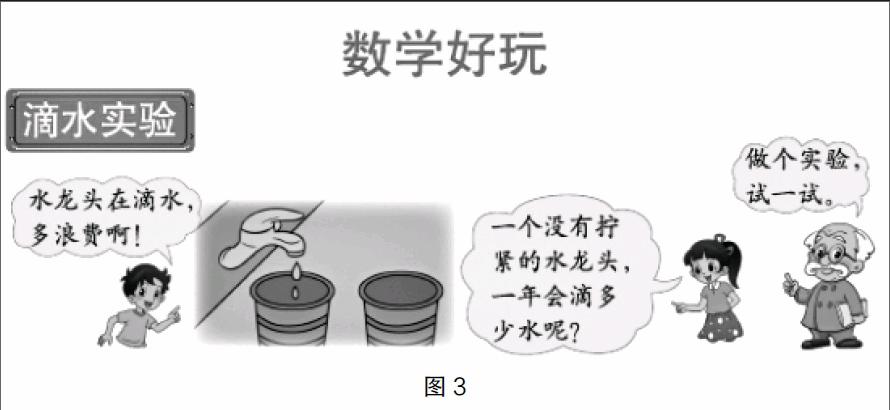
【案例】“滴水实验”教学片段（新北师大版小学数学四年级上册）

出示问题情境：

师：同学们，一个没有拧紧的水龙头一年会滴多少水呢？

生：我觉得有好几吨。

生：我觉得可以给我一家人用一个星期？

师：对于这个问题，你有办法算出来吗？

生：可以。先算出一个没有拧紧的水龙头一天滴水的量，然后再乘以365就可以了。

师：这个实验要做一天？太长了呀？还有其他的办法吗？

生：先算出一个没有拧紧的水龙头一小时滴水的量。

师：嗯，这样简单多了。但是一节课才40分钟，我们还是完成不了呀。

生：那就先算出一个没有拧紧的水龙头一分钟滴水的量吧。

师：一分钟？你们觉得可行不。

生：我觉得可行。

师：老师已经给你们每一个组准备了实验器材。请你们四人一组开展数学实验。先设计实验方案，再开展具体实验，最后得出实验结论。

一个没有拧紧的水龙头一年会滴多少水是一个实际问题，这个问题可以通过滴水实验来解决。能不能用更短的时间求出一年的滴水量呢？在教师与学生互动交流的过程中，学生想到了先算一天、一小时、一分钟的方法。在这个过程中，学生对化归思想就能够进行有效感悟，从而收到很好的教学效果。

总之，“数学好玩”栏目是提升学生数学素养的有效平台，在这一板块的教学中，教师要善于引导学生在数学操作、数学探究、数学实验的过程中对数学思想方法进行领悟。以上，笔者结合教学实例论述了在“数学好玩”栏目教学中让学生领悟分类思想、有序思想、化归思想的策略与方法，其实，数学思想方法包含内容远远不止这三种，教师要善于根据具体的教学内容进行灵活选择，合理运用，从而对小学生进行数学思想方法的渗透。endprint