信度函数在复杂网络节点重要性评价中的应用*

莫 泓 铭

(四川民族学院 图书馆，四川 康定 626001)

0 引 言

近年来，涌现了复杂网络这一新兴学科，来自数学、物理、计算机、生物等领域的研究者掀起了复杂网络的研究高潮[1-2]。与生活紧密相关的许多应用系统都可以被抽象建模并运用复杂网络理论来分析研究，如神经网络[3]、铁路网[4]、电力网[5]、人脑网络[6]、社交网络[7]等。运用复杂网络理论知识来研究这些现实生活中的复杂系统，可以实现高效率地管理、维护系统，提高系统可靠性与运行效率。节点重要度研究作为复杂网络众多研究内容的热点之一[8-14]，有利于进一步理清系统结构，对重要节点加以重点保护与维护，提升管理效率，增强系统鲁棒性。由于节点是具有多属性的，因而如何合理地利用各节点的相关属性更加快速准确地识别出重要的节点具有重要的现实意义。

证据理论Dempster-Shafer Theory of Evidence是Dempster于1967年首次提出[15]的，其学生Shafer于1976年对该理论进行了进一步推广[16]，目前已成为一种重要的不确定信息表达与处理工具。证据理论是传统贝叶斯概率论的推广，不仅可以表达单子集上的概率，并且可以表达多子集上的概率，不需要任何先验信息。证据理论还能准确地表达“不确定”与“不知道”等信息，这些在传统的概论率中是无法表达的。由于其能灵活地表达与处理不确定信息，已被广泛运用于信息融合、模式识别、图像分析、目标识别和决策分析等领域[17-21]。信度函数是证据理论的一种特殊表现形式[22-23]。信度函数已被广泛地运用于作战效能分析[24]、决策分析[25-26]等领域。节点是具有多属性的，复杂网络中节点的重要性评价可以视做多目标决策问题。为了更准确、更合理地探讨评价复杂网络中节点的重要性问题，提出了一种基于信度函数的评价方法，应用于无权无向的复杂网络，探讨复杂网络的节点重要度，将节点的相关属性构建为同一框架下的多个信度函数，并运用信度函数的融合工具进行融合，得到节点的综合重要度评价，并通过实例仿真分析说明了方法的有效性和优越性。

1 信度函数理论

证据理论[15-16]是一种新的、更灵活的信息，特别是不确定信息表达工具。证据理论不同于传统的贝叶斯概率论，它不需要先验信息，并且将传统概率的单子集赋值拓展到了单子集的幂集空间。

定义1 假设Θ={θ1，θ2，θ3，…，θn}是一个有限的非空互斥集合，证据理论中的辨识框架由该集合的所有子集构成，即Ω={∅，θ1，θ2…θi…θn，{θ1，θ2}，{θ1，θ3}…Θ}。该框架上的基本概率指派函数(Basic Probability Assignment，BPA)m(A)满足以下条件：

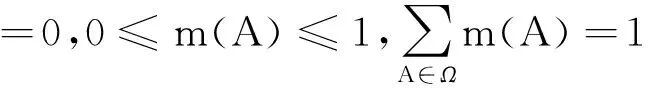
其中，∅是空集，A是集合Ω的任意子集。

信度函数作为证据理论中的一种特殊的BPA表现形式，其定义如下：

定义2 信度函数(Belief Function)Bel(A)表示所有明确支持命题A的BPA之和，即：

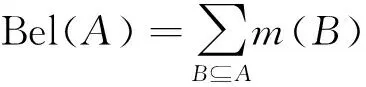
定义3 似然函数(Plausibility function)Pl(A)表示不否定命题A的BPA之和，即：

很明显，信度函数与似然函数有如下对应关系：

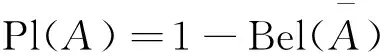
定义4 信任度区间Bel(A)，pl(A)表示命题A的信任区间，Bel(A)表示信任函数为下限，pl(A)表示似然函数为上限。Pl(A)与Bel(A)之差反映了命题A的不确定程度，数值越大，命题A的不确定程度就越大，数值越小，命题A的不确定程度就越小。

定义5 Dempster组合规则是证据理论的核心，它能够将两个原始的相互独立的BPA融合并生成一个新的BPA。Dempster组合规则或称为两个BPA的正交和。Dempster组合规则如下：

(1)

其中，k是冲突系数，反映两个BPA的差异化程度。当k=0时，意味着两个BPA是完全一样的。当k=1时，代表两个BPA是完全不一样的，即彼此互相矛盾，Dempster组合规则不能应用于此情形。Dempster组合规则具有良好的数学基础，满足交换律和结合律，即

m1⊕m2=m2⊕m1

(m1⊕m2)⊕m3=m1⊕(m2⊕m3)

因此，当多个BPA需要融合时，可以不用考虑其先后顺序而一对一对地进行融合。

2 复杂网络及相关节点重要度算法

现实生活中的许多系统都可以抽象建模为网络。网络由节点和边的关系构成。假如一个网络G=(V，E)，是由|V|=n个节点和|E|=m条边组成[27]。在无向无权图中，vij=1表示节点i和节点j之间有一条连边，vij=0代表节点i和节点j不相连。

2.1 复杂网络基本特征

复杂网络具有自组织、自相似、吸引子、小世界、无标度等特性[1-2]。复杂网络之“复杂”特性主要体现在：

(1) 复杂的网络拓扑结构、错综复杂的节点间关系。节点数量众多，节点与节点之间或存在多样化的有关系，比如在有向有权网络中，节点间的权重差异，节点与节点的方向性关系等。

(2) 对于时域或空域网络，点、边的状态随时间或空间的变化而变化。

(3) 多属性关系。复杂网络中的点、边都不是孤立存在的，都具有多重属性，因而很难简单的概括、描述其结构。

2.2 常见的复杂网络节点重要度算法

衡量节点的重要度的标准有很多，相应的识别算法也有很多，这些算法都从不同的角度出发来探讨节点的重要度问题。如何识别节点的重要度一直是当前的研究热门问题，近年来研究者们提出了许多的识别复杂网络中重要节点的算法，典型的中心型算法如下。

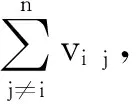
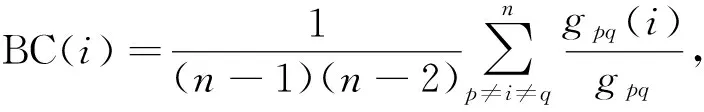
以上这些算法都是从某个特定的角度出发来衡量节点的能力，每种算法都有其适用性与局限性。Du等基于TOPSIS法来综合考虑了节点的DC、BC、CC等属性指标，并据此得到节点的重要性排序结果等[30]。相关研究表明：节点重要性程度除了与其自身影响力有关之外，还与其所处的位置也有密切相关，即使某个节点的邻居非常少，但它处在网络的核心位置，非常重要。相反，某些处在网络边缘的节点，虽然其度很大，但其影响力却很小。Kitsak等提出了K核分解算法，通过将网络剥离分层的方式来评价节点的重要能力[31]。K核分解法在分析大规模网络的层次结构等方面有较好的适用性，然而也存在一定的局限性，研究者们不断地改进K核算法，并取得了一定成果。此外，还有PageRank 算法[32]、LeaderRank算法[33]、Efficiency Centrality[34]、AHP方法[35]等。

3 信度函数的节点重要度识别模型

基于信度函数构建复杂网络中的重要节点识别模型，其具体步骤如下。

步骤1 构建统一的辨识框架，将节点的相关属性值在统一的辨识框架下进行转换。

步骤2 结合网络实际情况，选择合适的节点属性指标，并测得各属性指标数值。

步骤3 构造信度函数，将节点的各属性指标值转换为信度函数的表现形式。

步骤4 融合信度函数，运用Dempster组合规则依次融合各信度函数，结果为一个信度函数。

步骤5 数值转换，将最终信度函数值转换成单一数值，并据此排序。

4 实例应用

以Football网络[36]为例来验证提出的基于信度函数评价方法的有效性和可行性。其网络结构如图1所示，该网络由35个节点和118条边组成，该网络是无向无权的。

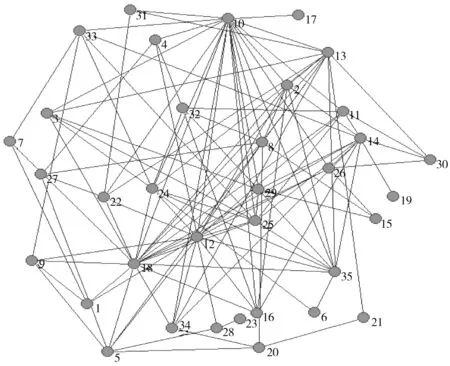
图1 Football网络结构示意图Fig.1 The network structure of Football

步骤1 构建信度函数的统一的辨识框架。在例中，节点重要与否简单划分为2类，即重要与不重要，分别用b和u表示，构建辨识框架θ={b，u}。

步骤2 选择测算指标。结合网络情况，节点的度、紧密度中心值、介数中心值等属性指标被选择来用于构建信度函数，通过相应的算法获得其对应值分别如表1中的第2、4、6列所示，第1列为节点编号。

步骤3 基于属性值的极值构造信度函数。以节点的度属性为例，选择节点度的最大值Degmax与最小值Degmin作为参考值，即有

Degmax=max{Deg1，Deg2…Degi…Degn}

Degmin=min{Deg1，Deg2…Degi…Degn}

其中，Degi为节点i的度属性值，Degmax为所有节点度属性值中的最大值，Degmin为所有节点度属性值中的最小值。

则，

Degi(θ)=1-Degi(b)-Degi(u)

其中，Degi(b)表示节点i重要性程度的大小，Degi(u)表示节点i不重要性程度的大小，Degi(θ)表示节点i的重要性与否未知。ε为调节性参数，ε∈(0，1]，其作用为防止出现当最大值与最小值相同时出现分母为0的非法情况，其值不影响最终结果，在例中，为简便，取ε=0.5。

以节点1的度属性为例，在Football网络中，由表1第2列可知，节点的度最大值与最小值分别为Degmax=19，Degmin=1，则有

Deg1(θ) =1-Deg1(b)-Deg1(u)=1-0.162 2-0.810 8=0.027 0

则节点1的度信度函数表示为

Deg(1)=(0.162 2，0.810 8，0.027 0)

(2)

同理可得，节点1的紧密度信度函数和介数信度函数表示分别为

Clo(1)=(0.168 3，0.585 7，0.246 0)

(3)

Bet(1)=(0.004 8，0.266 3，0.728 9)

(4)

相似地，可以得到余下节点的度信度函数、紧密度信度函数和介数函数，限于篇幅，本部分略。

步骤4 融合各节点的属性信度函数值。由于Dempster组合规则具有交换性与结合性，以节点1为例，可以不分先后地融合节点1的度中心信度函数、紧密度中心信度函数和介数中心信度函数值。首先融合节点的度与紧密度，结合式(1)，由式(2)、式(3)有

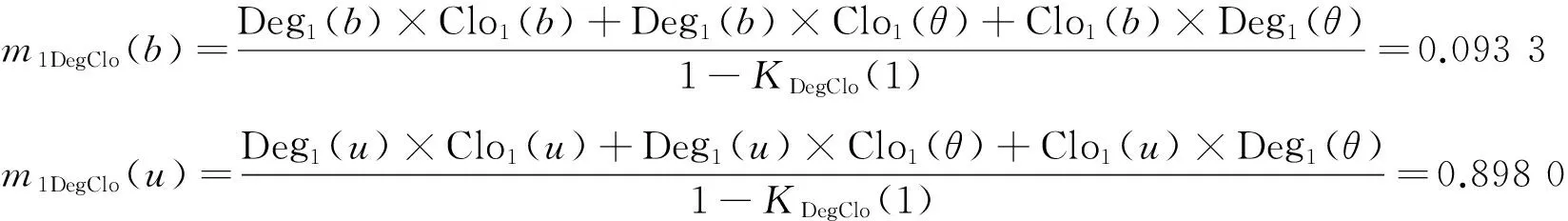
即

m1DegClo=(0.093 3，0.898 0，0.008 7 )

(5)

相应地，基于式(1)，结合式(4)、式(5)，可得到节点1的最终的综合信度函数为

m1=(0.070 6，0.922 9，0.006 5)

(6)

步骤5 综合信度函数转换。在获得节点的综合信度函数后，需将该组数值转换为单一数值，以便进一步比较其数值大小，其转换公式如下：

m(i)=mi(b)-mi(u)

(7)

其中，mi(b)为节点i关于参数b的信度函数，mi(u)为节点i关于参数u的信度函数。对于未知部分mi(θ)可以忽略不计或平均分配给参数b和u，在例中，采用平均分配的方法。

以节点1为例，有

类似地，可以得到其他节点的属性最终值，如表1第8列所示。

表1 Football网络节点相关属性值Table 1 Values of attributes of nodes of Football network

5 实验讨论

表1的第3、5、7、9列分别代表度中心算法、紧密度中心算法和邻近度中心算法的排序结果。由表1可知，不同的算法所得到的排序结果是不一样的。在度中心算法中，35个节点，一共识别出了15个不同的度，有许多节点拥有相同的度，因而度算法无法区分这些具有相同度的节点的重要性。紧密度中心算法主要从节点在网络全局中的位置出发，较度中心算法能更好地识别节点的重要程序，然而仍然存在无法识别的情况，如节点8、25、35。同时，某些度较大的节点在紧密度算法中却呈现排名较后的情况，如节点14的度为12，在紧密度中心算法中排名第10，而节点2的度为8，在紧密度中心算法中排名第5。因而紧密度中心算法与度中心算法无明确关联性。介数中心算法相对于度中心算法与紧密度中心算法而言，能更加细化地识别不同节点的重要程序，然而仍然存在无法进一步细分的情况，如节点6、17、19、23、31。介数中心算法更多地是考虑节点在网络全局最短路径中的地位，即使节点存在相同的度，但由于其并非处于网络最短路径的主干线路中，其重要程度也是不一样的，如节点7、15、28、31，因而介数中心算法与度中心算法无明确关联性。介数中心算法与紧密度中心算法所识别的最重要节点分别是节点12与节点18。节点2在紧密度中心算法中排名第5而在介数中心算法中却排名第19，以上表明介数中心算法与紧密度中心算法亦无明确关联。由上述分析可知，度中心算法、紧密度中心算法和介数中心算法彼此无明确关联性，彼此独立，满足Dempster组合规则的先决条件，可以被运用于融合节点的这3种属性，进而本文构建的模型具有合理性。

Football网络中的35个节点经本文提出的算法融合后产生了35个不同的结果，如表1第8列所示，充分地识别了每一个节点的重要性程序，解决了度中心算法、紧密度中心算法和介数中心算法无法识别某些节点重要性的问题。此外，这4种算法所识别的网络中前4个重要的节点是一样的，尽管由于各中心算法的侧重点不同导致排序上有少许差异，以上仍表明了模型的有效性。

6 结 语

基于信度函数构建了复杂网络中节点重要度评价模型，并结合Football网络进行实例验证了模型的有效性。模型主要是采用节点的相关属性并将其转换为信度函数，然后运用Dempster组合规则来融合节点的相关属性，得到节点的一组综合信度函数值，然后将其转换为一个单一的数值，并依此对节点的影响力进行排序，克服了单一属性方法有时无法区别具有相同属性值的节点的影响力的情况。实例验证表明：模型具有合理性和有效性。研究有一定的理论意义与现实意义，可进一步推广到其他网络及更多的节点属性。如何根据网络特征合理选择节点的属性算法是下一步的研究方向。

[1] STROGATZ S H.Exploring Complex Networks[J].Nature，2001，410： 268-276

[3] 李倩，李东，王娴.分数阶 BAM 神经网络的全局渐进稳定性[J].重庆工商大学学报(自然科学版)，2017，34(1)： 21-26

LI Q，LI D，WANG X.Global Asymptotic Stability of Fractional-order BAM Neural Networks[J].Journal of Chongqing Technology and Business University(Natural Science Edition)，2017，34(1)： 21-26

[4] 徐青，何松，魏可可，等.基于复杂网络理论的地铁深基坑施工事故致因研究[J].安全与环境工程，2017，24(1)： 152-157

XU Q，HE S，WEI K K，et al.Research on Causes of Accident in Deep Foundation Pit Construction Based on Complex Network Theory[J].Safety and Environmental Engineering，2017，24(1)： 152-157

[5] 王轶楠，林彦君，李焕.DoS 攻击下电力网络控制系统脆弱性分析及防御[J].控制与决策，2017，32(3)： 411-418

WANG Y N，LIN Y J，LI H.Vulnerability Analysis and Countermeasures of Electrical Network Control Systems under Dos Attacks[J].Control and Decision，2017，32(3)： 411-418

[6] 唐书辉，卿鹏.睡眠剥夺下人脑功能脑网络分析[J].重庆工商大学学报(自然科学版)，2016，33(6)： 31-35

TANG S H，QING P.Analysis of Human Cerebral Function and Brain Network under Sleep Deprivation[J].Journal of Chongqing Technology and Business University(Natural Science Edition)，2016，33(6)： 31-35

[7] 李亚平.有限实名网络中个体行为分析与建模[J].重庆工商大学学报(自然科学版)，2016，33(4)： 79-85

LI Y P.Analysis and Modeling of Individual Behavior in the Limited Real Name Network[J].Journal of Chongqing Technology and Business University(Natural Science Edition)，2016，33(4)： 79-85

[8] WEI D J，DENG X Y，ZHANG X G，et al.Identifying Influential Nodes in Weighted Networks Based on Evidence Theory[J].Physica A，2013，39(10)： 2564-2575

[9] GAO C，WEI D J，HU Y，et al.A Modified Evidential Methodology of Identifying Influential Nodes in Weighted Networks[J].Physica A，2013，39(21)： 5490-5500

[10] 莫泓铭.节点重要度在复杂网络鲁棒性中的应用[J].长春师范大学学报，2016，35(2)： 22-25

MO H M.An Application of the Nodes Importance in Network Robustness[J].Journal of Changchun Normal University，2016，35(2)： 22-25

[11] YIN L K，ZHENG H Y，BIAN T，et al.An Evidential Link Prediction Method and Link Predictability Based on Shannon Entropy[J].Physica A，2017，48： 699-712

[12] LÜ L Y，CHEN D B，REN X L，et al.Vital Nodes Identification in Complex Networks[J].Physics Reports，2016，65： 1-63

[13] LIU Y，TANG M，ZHOU T，et al.Identify Influential Spreaders in Complex Networks the Role of Neighborhood[J].Physica A，2016，452： 289-298

[14] LIU J H，ZHU Y H，ZHOU T.Improving Personalized Link Prediction by Hybrid Diffusion[J].Physica A，2016，44： 199-207

[15] DEMPSTER A P.Upper and Lower Probabilities Induced by A Multivalued Mapping[J].The Annals of Mathematical Statistics，1967，50： 325-339

[16] SHAFER G.A Mathematical Theory of Evidence[M].Princenton：Princeton University Press，1976

[17] DENG Y.D Numbers： Theory and Applications[J].Journal of Information and Computational Science，2012，9(9)： 2421-2428

[18] DENG Y.Generalized Evidence Theory[J].Appl Intell，2015，43(3)： 530-543

[19] 莫泓铭，夏龄.基于证据理论的川西水电开发生态环境评价研究[J].长春师范大学学报，2017，36(2)： 35-40

MO H M，XIA L.An Evidence Theory Based Evaluation of Influence on Ecological Environment among Hydropower Development in Western Sichuan[J].Journal of Changchun Normal University，2017，36(2)： 35-40

[20] DENG Y.A Threat Assessment Model under Uncertain Environment[J].Math Probleng，2015，2015(9)： 1-12

[21] DENG X Y，HU Y，DENG Y，et al.Environmental Impact Assessment Based on D Numbers[J].Expert Syst Appl，2014，41(2)： 635-643

[22] 王占斌，赵辉，齐红丽，et al.基于信度函数的冲突证据组合新方法[J].上海理工大学学报，2008，30(1)： 50-54

WANG Z B，ZHAO H，QI H L，et al.New Combination Approach Based on Creditability Function for Conflict Evidences[J].Journal of University of Shanghai for Science and Technology，2008，30(1)： 50-54

[23] 王霞，田亮.基于典型样本的信度函数分配的构造方法[J].电力科学与工程，2015(5)： 11-15

WANG X，TIAN L.Method of Constructing Confidence Function Distribution Based on Typical Sample[J].Electric Power Science and Engineering，2015(5)： 11-15

[24] 李志军，王巨海，郭栋.信度函数在作战效能分析中的运用[J].指挥控制与仿真，2006，28(1)： 41-43

LI Z J，WANG J H，GUO D.Application of Belief Function for Combat Effectiveness Analysis[J].Command Control & Simulation，2006，28(1)： 41-43

[25] 杨春，李怀祖.基于信度函数的决策方法探讨[J].系统工程，2000，18(2)： 66-72

YANG C，LI H Z.On Decision Approaches Based upon Belief Function[J].Systems Engineering，2000，18(2)： 66-72

[26] 蒋雯，张安，邓勇.基于信度函数的决策及应用[J].计算机工程与应用，2008，44(31)： 36-38

JIANG W，ZHANG A，DENG Y.Decision Making Based on Belief Function[J].Computer Engineering and Applications，2008，44(31)： 36-38

[27] FREEMAN L.Centrality in Social Networks Conceptual Clarification[J].Social Networks，1978，1(3)： 215-239

[28] ALBERT R，JEONG H，BARABSI A. Diameter of the World-Wide Web[J].Nature，1999，40： 130-131

[29] FREEMAN L C.A Set of Measures of Centrality Based on Betweenness[J].Sociometry，1977： 35-41

[30] DU Y X，GAO C，HU Y，et al.A New Method of Identifying Influential Nodes in Complex Networks Based on Topsis[J].Physica A，2014，39： 57-69

[31] KITSAK N，GALLOS L K，HAVLIN S，et al.Identification of Influential Spreaders in Complex Networks[J].Natphys，2010，6(11)： 888-893

[32] PAGE L，BRIN S，MOTWANI R，et al.The Pagerank Citation Ranking： Bringing Order to the Web [R].Stanford InfoLab，1999

[33] LÜ L Y，ZHANG Y C，YEUNG C H，et al.Leaders in Social Networks，the Delicious Case[J].Plos One，2011，6(6)： 212-202

[34] WANG S S，DU Y X，DENG Y.A New Measure of Identifying Influential Nodes： Efficiency Centrality[J].Commun Nonlinear Scl，2017，47： 151-163

[35] BIAN T，HU J T，DENG Y.Identifying Influential Nodes in Complex Networks Based on AHP[J].Physica A，2017，47： 422-436

[36] Bouchard A.Link Analysis and Visualization[J].Drdc Valcartier TM，2004，75：175-180