考虑轴线偏差的多平行轴齿轮动态啮合力分析

吴玉红，张 昊，俞迎丹，韩清凯

（大连理工大学 机械工程学院，辽宁 大连 116024）

1 引言

离心压缩机是大型旋转机械中最具有代表性的机组之一，广泛应用于冶金，石油化工等领域，是体现国家装备制造业水平的一个标志[1]。齿轮-转子系统是多轴齿轮组装式离心压缩机的核心部分，其动力学性能直接体现了压缩机系统的动力学性能。轴线偏差是齿轮轴的常见误差，主要是由于支承不对中，制造误差，齿轮轴受力变形等原因造成。齿轮轴线偏差，不仅会影响转子的动力学特性，而且会改变齿轮间的接触状态，对齿轮的工作性能产生影响，如噪声与振动、齿轮的部分接触、传动精度等[2]。因此，为了提高压缩机设备的工作性能，轴线偏差故障下齿轮-转子系统动力学特性的研究具有非常重要的意义。

国内外学者对于齿轮误差特别是轴线偏差进行了大量的研究。文献[3]以一对修形直齿轮为研究对象，建立了其轴线偏差有限元模型，并研究了修形参数对其疲劳性能的影响。文献[4]对直齿轮在静态和动态工况下的齿根应力变化进行了实验研究。文献[5-6]采用有限元和实验法对齿轮轴线偏差引起的齿轮载荷分布以及弯曲应力状况进行分析，并考虑齿向修形的影响，结果表明齿向修形能改善齿轮在轴线偏差引起的偏载等现象。文献[7]利用虚拟样机考虑了装配误差对风电齿轮箱动载系数的影响规律利用。文献[8]考虑了轴不对中对蜗杆机构齿轮载荷分布以及传递误差的影响。

目前，对于齿轮轴线偏差的研究大都局限于针对齿轮副采用有限元静力分析法或实验法进行分析，其中，有限元静力分析未考虑到旋转效应以及支承的影响，而实验法更是无法排除轴承间隙、齿轮制造误差等带来的影响。针对五轴齿式离心压缩机，采用ADAMS建立了五平行轴齿轮转子系统模型，考虑了轴系的旋转效应、载荷、齿轮啮合冲击等影响，研究了轴线偏差故障对齿轮啮合力的影响规律。

2 研究对象

以五轴齿轮组装式离心压缩机转子系统为研究对象，其结构示意图，如图1所示。力学模型，如图2所示。

图1 离心压缩机转子系统结构示意图Fig.1 The Sketch of the Centrifugal Compressor Rotor System

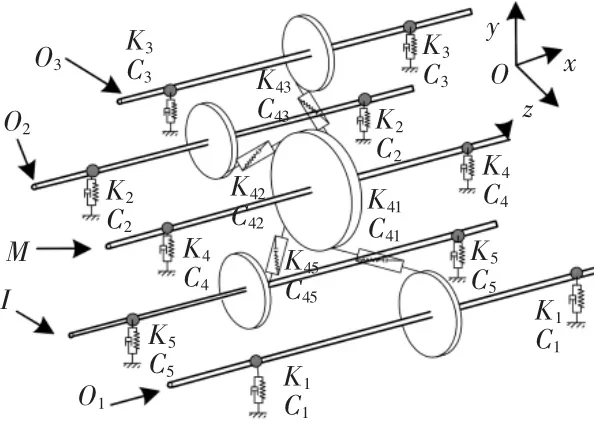
图2 离心压缩机转子系统力学模型图Fig.2 Dynamic Model of the Centrifugal Compressor Rotor System

3 轴线偏差故障

文献[9]中规定了轴线精度包括中心距和轴线平行度。以齿轮轴O1为例，轴线偏差定义，如图3所示（其余齿轮轴未在图中显示）。轴线平面内偏差f∑β是两轴公共平面内测得的，如图3（a）所示。垂直面内偏差f∑β是在过轴承中心、垂直于公共平面且平行于轴线的平面上测得的，如图3（b）所示。中心距偏差fa是实际安装中心距与设计中心距的偏差值，并规定中心距偏差靠近轴M为负，远离为正，如图 3（c）所示。

图3 中心距偏差与轴线平行度偏差示意图Fig.3 Sketch of the Center Distance Error and Parallelism Error

4 模型建立与验证

4.1 ADAMS模型

为了研究五轴齿式离心压缩机转子系统的动力学特性以及轴线偏差故障下的啮合力特性，采用ADAMS虚拟样机建立了该齿轮系统的动力学仿真模型，其中参数，如表1所示。

表1 齿轮轴结构参数Tab.1 Parameters of the Gear Shafts

齿轮的压力角为20°，倾斜角为12°，模数为2.5。模型采用的材料参数为：密度7.8g/cm3，泊松比0.29。据齿轮传动的运动规律，模型中加入的约束和载荷，如下：（1）轴承用轴套单元来模拟，施加在轴承两端与大地之间，轴承拉伸刚度为1e5N/mm，轴承阻尼为10N/（mm/s）；（2）在输出轴O1、O2、O3上施加转矩，模拟负载；（3）在输入轴I支承端施加绕z轴旋转的点驱动；（4）齿轮之间施加碰撞接触力，以实现齿轮的啮合传动。接触参数的合理性是齿轮仿真正确的重要因素，考虑到收敛性和仿真速度，取力指数e=1.5，啮合阻尼10N/（s·mm），侵入深度值0.1mm。考虑齿轮之间的摩擦，取动摩擦系数0.05，静摩擦系数0.08，静阻力滑移速度0.1mm/s，动阻力转化速度10mm/s。以赫兹静态接触理论为基础推导计算接触刚度系数，啮合刚度系数K计算式：

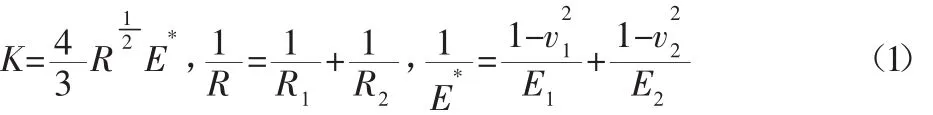
式中：K—刚度系数；R—综合曲率半径；E*—综合弹性模量；E1、

E2—两物体材料弹性模量；v1、v2—两物体材料泊松比；R1、

R2—两物体接触点的当量曲率半径，可用分度圆半径来代

替齿轮接触点当量半径。

计算得到齿轮的刚度系数，如表2所示。获得的五轴齿式压缩机的ADAMS模型，如图4所示。为了验证ADAMS模型的正确性，从转速以及啮合力两个方面对模型进行验证。

表2 啮合刚度系数表Tab.2 Parameters of Meshing Stiffne ss

图4 ADAMS模型Fig.4 ADAMS Model

4.2 模型验证

4.2.1 转速

输入轴采用step函数输入转速，速度函数表达式为step（time，0，0，0.1，20*360d），表示在（0～0.1）s内转轴角速度从0升到20Hz。仿真得到各轴的转速仿真情况，如图5所示。

图5 齿轮转速图Fig.5 Gear Rotating Speeds

4.2.2 啮合力

式中：T—齿轮传递的扭矩；Ft—切向力；Fr—径向；Fa—轴向力。

根据齿轮轴O1与中间轴M为例验证接触参数的正确性，在O1处施加10Nm的反扭矩来模拟负载情况。规定的差异率λ=

斜齿轮啮合力在切向、轴向及径向分量的计算，如式（2）所示。，比较啮合力理论值与仿真均值，如表3所示。由表3的差异率可知，齿轮啮合力误差控制在3%以内，说明仿真参数设置的正确性。

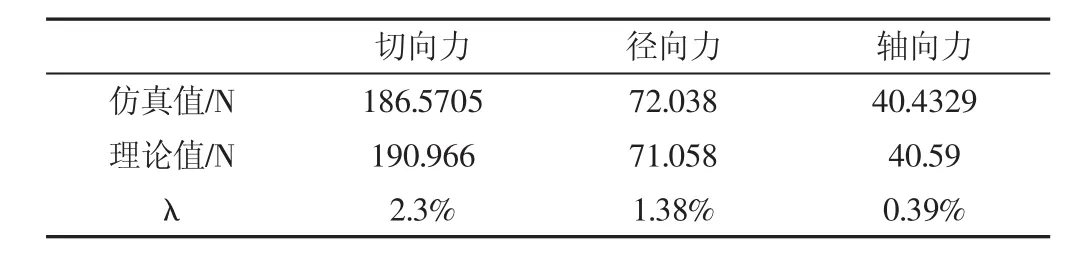
表3 O1-M啮合力比较Tab.3 O1-M Meshing Force Comparison

齿轮正常啮合的情况下会产生齿轮啮合频率，啮合频率的计算公式为：fz=Z·n/60 （3）

式中：fz—啮合频率值（Hz）；Z—齿数；n—转速（r/min）。

在输入轴施加10Hz转速，理论啮合频率为800Hz，仿真得到M与O1啮合力频域，如图6所示。可以看到，频域上啮合频率以及其倍频成分与理论分析一致。

图6 啮合力频域图Fig.6 Meshing Force Frequency Domain Results

5 仿真分析

5.1 轴线平行度偏差

为了比较不同载荷和平行度偏差量下齿轮啮合力的变化规律，以齿轮轴O1为例，设置了五种偏差量（0mm，0.25mm，0.5mm，0.75mm，1mm）和三种载荷（10Nm，20Nm，25Nm），并进行了动力学仿真分析。为了对比正常啮合状态和轴线平行度偏差下的时域与频域，设置输入轴转速为10Hz，O1负载为25Nm进行动力学仿真图略。对比三种工况下的时域图，可以看到当存在轴线偏差时啮合力振动幅值比正常啮合状态下的振动幅值有所增大，这是由于轴线偏差下齿轮的碰撞冲击严重导致。频域上，正常啮合状态时以啮合频率为主，1/2倍频和1/4倍频为辅，当存在轴线偏差时频域上1/2倍频和1/4倍频的成分变大，啮合频率成分变小，垂直平面平行度偏差下甚至出现了1/8倍频成分，可见轴线偏差故障使齿轮非线性更加明显。

5.1.1 轴线平面平行度偏差

以O1为例设置不同的轴线平面平行度偏差值，得到不同载荷与偏差量下啮合力均值与振动幅值的变化规律，如图7所示。由图8（a）可以看到在不同的轴线平面平行度偏差下，齿轮啮合力均值基本保持不变。从啮合力振动幅值上看，随着偏差量的增大可以看到齿轮啮合力振动量有明显的增大趋势，这是由于轴线平面平行度偏差使齿轮副间隙发生变化，引起一端齿面的干涉，增大了齿轮啮合的振动冲击，振动幅值变大。由于碰撞冲击振动幅值甚至增大到均值的（5-6）倍。对比三种载荷下振动幅值的变化趋势可以看到负载越大，变化越平缓，说明负载增大使齿轮之间啮合力变大，齿轮之间的啮合作用减小了由轴线偏差引起的碰撞冲击。

图7 轴线平面平行度偏差下啮合力平均值与幅值Fig.7 Mean Values and Amplitudes of the Meshing Force Under Axis Plane Parallelism Errors

5.1.2 垂直平面平行度偏差

与轴线平面平行度偏差类似，以O1为例设置不同的垂直平面平行度偏差值，得到不同载荷与偏差量下啮合力均值与振动幅值的变化规律，如图8所示。

图8 垂直平面平行度偏差下啮合力平均值与幅值Fig.8 Mean Values and Amplitudes of the Meshing Force Under Vertical Plane Parallelism Errors

如图8所示，垂直平面平行度偏差下齿轮啮合力的变化规律与轴线平面平行度偏差的规律类似，随着偏差量的增大，啮合力的均值无明显变化，振动幅值明显变大，且负载越小，振动幅值变化趋势越明显。由上述结果可知，平行度偏差主要引起了齿轮啮合力振幅变大，对比两种偏差下齿轮啮合力的振动幅值，以20Nm以及25Nm为例结果，如图9所示。为表达方便，规定X为轴线平面平行度偏差，Y为垂直平面平行度偏差。

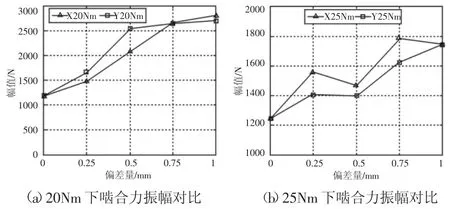
图9 两种平行度偏差下的啮合力振幅对比Fig.9 Meshing Force Amplitude Comparison Under Two Kinds of Parallelism Errors

5.2 中心距偏差

为了研究不同载荷和中心距偏差量下的齿轮啮合力特性，与轴线平行度偏差类似，设置了三种载荷（10Nm，20Nm，25Nm）和六种中心距偏差量，其中包括一种负偏差量（-0.5mm）、四种正偏差量（0.25mm，0.5mm，0.75mm，1mm）和正常状态。设置输入轴转速为10Hz，O1负载为25Nm进行动力学仿真，对比正常啮合状态和中心距偏差下的时域与频域（图略）。与正常啮合状态相比，正中心距偏差下，啮合力并没有明显的变化，频域上啮合频率为主，二倍频以及1/2倍频为辅；负中心距偏差下，频域上无明显变化，但时域上幅值有所变大。以O1为例设置不同的中心距偏差值，得到不同载荷与偏差量下啮合力均值与幅值的变化规律，如图10所示。

图10 不同中心距偏差下的啮合力均值与幅值Fig.10 Mean Values and Amplitudes of the Meshing Force Under Center Distance Errors

由图10（a）可知，其啮合力的均值随着中心距的变大，无明显变化，可见，中心距的变化虽然改变了齿轮的重合度，但是由于结构的自动补偿功能，中心距稍有偏差时，并不会引起啮合力均值的剧烈变化。

由图10（b）可知，当存在负中心距偏差时齿轮啮合力的振动幅值变大，这是由于中心距变小，齿轮间隙变小，齿轮轴O1的齿顶与中间齿轮轴之间相互干涉，增大了碰撞冲击，故啮合力振动幅值变大。但当存在正中心距偏差时，可以看到载荷在10Nm时振动幅值随着偏差量的变大而变小。10Nm载荷下中心距变大1mm时振动幅值减小了20.2%。对比10Nm工况下e=0和e=0.5齿轮轴O1的转动加速度，如图11所示。对比两种工况的冲击最大值，可以看到e=0时的反向碰撞冲击引起的转动加速度远大于e=0.5工况。可见由于中心距的变大使齿轮间的侧隙变大，在齿轮轻载状况下，齿轮双面碰撞冲击由于间隙变大而有所缓解，故啮合振动幅值随着偏差量的增大而降低。增大载荷，齿轮啮合力变大，齿轮反向碰撞减小，因此在20Nm和25Nm载荷下正中心距偏差对于齿轮啮合力影响不明显。

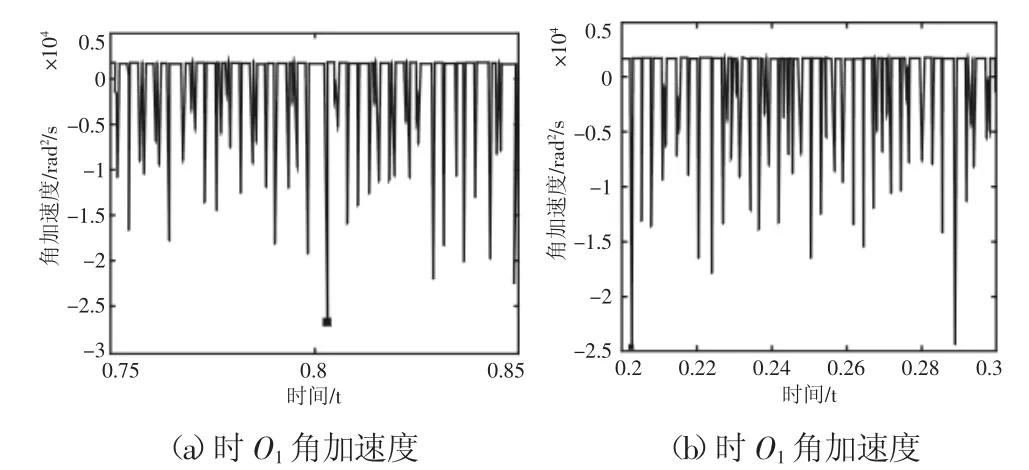
图11 O1两种中心距偏差下角加速度时域图Fig.11 Angular Acceleration Time-Domain Results Under Two Kinds of Center Distance Errors

6 结论

（1）轴线平行度偏差加剧了齿轮轴的非线性现象，随着偏差量的增大频域上1/2倍频和1/4倍频的成分变大，啮频成分变小，非线性现象明显；（2）在两类平行度偏差下，齿轮啮合力均值均变化不明显，但齿轮啮合力振动幅值有明显的增大趋势，且负载越大啮合力振动幅值变化趋势越不明显；（3）两种平行度偏差下的啮合力振动幅值与其载荷有关，轻载下垂直平面引起的冲击更大，重载下反而相反，可见重载对垂直平面平行度偏差引起的振动冲击抑制作用更明显；（4）中心距偏差对齿轮啮合力频域成分无明显影响，负中心距偏差下齿轮碰撞加大，啮合力振动幅值增大；正中心距偏差下，由于齿轮间隙变大，缓解了轻载下的齿轮的双面碰撞冲击，啮合力振动幅值减小，但载荷增大后啮合力振幅无明显变化。

［1］夏勃然，托西.离心压缩机转子动力学［J］.风机技术，1992（5）：20-22.（Xia Bo-ran，Tuo Xi.Centrifugal compressor rotor dynamics［J］.Compressor Blower and Fan Technology，1992（5）：20-22.）

［2］高雪官，辛一行，王统.齿形参数对齿轮摩擦学性能的影响分析［J］.机械设计与研究，1994（3）：24-36.（Gao Xue-guan，Xin Yi-xing，Wang Tong.Analysis of gear tooth parameters effect on the tribological properties［J］.Machine Design and Research，1994（3）：24-36.）

［3］K.Mao.Gear tooth contact analysis and its application in the reduction of fatigue wear［J］.Wear，2007（262）：1281-1288.

［4］Kubo，A.Stress condition，vibration exciting force and contact pattern of helical gear with manufacturing errors［J］.ASME Journal of Mechanical Design，1978（100）：77-85.

［5］M.Hotait，A.Kahraman.Experiments on root stresses of helical with lead crown and misalignment［J］.ASME Journal of Mechanical Design，2008，130（7）：1-5.

［6］M.Hotait，A.Kahraman，T.Nishino.An investigation of root stresses of hypoid gears with misalignments［J］.ASME Journal of Mechanical Design，2011（133）：1-9.

［7］杨为，孙宏，黄一林.装配误差对风电齿轮箱动载系数的影响规律研究［J］.机械设计与制造，2012（11）：66-68.（Yang Wei，Sun Hong，Huang Yi-lin.Research on influences of assembly errors to wind gearbox dynamic load coefficient［J］.Machinery Design＆Manufacture，2012（11）：66-68.）

［8］Vilmos V.Simon.Influence of tooth errors and shaft misalignments on loaded tooth contact in cylindrical worm gears［J］.Mechanism and Machine Theory，2006（41）：707-724.

［9］GB-Z 18620.3-2008，圆柱齿轮检验实施规范第3部分：齿轮坯、轴中心距和轴线平行度的检验［S］.（GB-Z 18620.3-2008，Cylindrical gears-code of inspection practice-Part 3：Recommendations relative to gear blanks，shaft center distance and parallelism of axis［S］.）