汽车动力学参数的相对灵敏度分析
汪永志,汪 伟,贝绍轶,张兰春
(江苏理工学院 汽车与交通工程学院,江苏 常州 213001)
1 引言
近年来,汽车主动安全技术成为研究热点,特别是备受瞩目的电子稳定性控制系统成为重中之重,该技术可以弥补驾驶员的操纵的局限性,实现紧急避让等极限工况下的主动安全。对于该技术的实现前提就是准确的预知汽车实时的状态参数,而对于此类参数的获取,由于其昂贵的传感器限制,目前的获取方法大多为软测量,即通过易测量结合一定的算法估计得到,即状态估计[1]。
目前很多状态估计研究算法采用了卡尔曼(KF)滤波及其衍生算法,该方法以其精度较高,实时性好而被广泛采用,同时研究过程中有两类模型,即动力学模型和运动学模型。运动学模型对传感器的精度要求比较高,而动力学模型对汽车自身结构参数的精度的要求比较高[2-3]。根据状态空间方程进行滤波估计后得到的状态量估计值的精度必然与汽车自身结构参数的精度有关,但是之前的研究中,并没有使用汽车状态参数对汽车结构参数的灵敏度进行探讨,所以旨在分析汽车状态参数对汽车结构参数的灵敏度,对汽车状态估计算法的研究提供理论参考。灵敏度的分析方法有很多种,但是对于的主要研究内容来说,一些常规的理论推导分析方法将会遇到很大的计算量,并且不一定能收到好的效果,采取简单易行的参数扰动法对研究内容进行分析。
该方法在线性二自由度汽车模型和卡尔曼滤波理论基础上,分析估计所得的状态量(横摆角速度、质心侧偏角)对动力学模型中的汽车的质量、转动惯量以及质心至前轴距离的灵敏度。该方法与以往的灵敏度分析方法不同,以往的灵敏度分析方法在已知模型之后通过各种方法分析模型中某参数的灵敏度,而需要利用参数扰动分析进行卡尔曼滤波之后所得的状态量来对汽车参数的灵敏度进行分析,算法简单,且通过实验数据验证所得的结果的可信度高。
2 汽车状态估计
2.1 汽车动力学模型
忽略转向系统的作用,直接以前轮转角作为输入,且仅考虑汽车沿y轴的侧向运动和绕z轴的横摆运动这两个自由度,汽车沿x轴的前进速度为匀速运动,侧向加速度在0.4g以下,轮胎侧偏特性处于线性范围,这样汽车简化为一个两轮摩托车模型,如图1所示。该动力学模型未引入复杂的轮胎模型,计算量相对较小,实时性好[4-5]。模型由式(1)~式(4)描述。
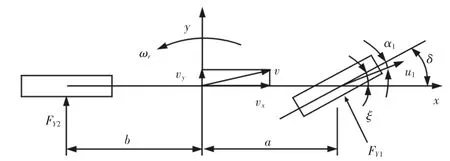
图1 汽车模型示意图Tab.1 Schematic Diagram of Automobile Model

由运动学的基本关系并结合图1,可得tanβ=vy/vx,由于β较小,则可得:β=vy/vx(4)
将式(1)~式(4)整理后得状态方程和观测方程如式(5)~式(6)所示。

式中:m—整车质量;Iz—整车对z轴转动惯量;a—质心到前轴的距离;b—质心到后轴的距离;k1—前轮侧偏刚度;k2—后轮侧偏刚度;vx—质心处纵向速度;vy—质心处侧向速度;δ—前轮转角;ax—纵向加速度;ay—侧向加速度;β—质心侧偏角;ωr—横摆角速度。
2.2 卡尔曼滤波算法
对于线性常规KF滤波算法,有如下内容[6]:

3 单因素扰动法
3.1 灵敏度分析方法的选择
导数的计算是灵敏度分析的基础,灵敏度的计算有直接微分法、伴随矩阵变量法、自动微分法、扰动法等[7]。若根据矩阵微分理论,灵敏度需要知道完整的矩阵方程后,对该方程求偏导,即:

若根据式(8),将式(5)~式(6)直接求偏导,则该过程由于KF滤波过程中有过程噪声和观测噪声存在无法反映估计过程对灵敏度的影响。若按照滤波理论过程进行完整的方程推导,然后根据级数展开进行前6阶级数展开,这样伴随着很大的计算量,而且展开过程中误差将会影响灵敏度的比较。目前国内外尚无在该方面的研究可以借鉴,而且ωr、β在汽车运行过程中是随时间历程变化的量,不同的工况ωr、β对参数m,a,Iz变化的敏感程度肯定不一样,例如:在直线行驶工况下,ωr、β 接近于零,m,a,Iz的变化在该工况下对ωr、β影响甚微[8]。如何寻找一种合适的分析方法与分析策略是的重点也是难点。
采用扰动法进行灵敏度分析,该方法不需要复杂的求导运算,即根据导数的意义,给自变量一个相对小的扰动,然后根据因变量在扰动前后的值之差与扰动量的比值来描述因变量对自变量的敏感程度。结合研究的模型考虑到汽车行驶过程中的过渡工况:转弯、单移线换道、双移线避让等等,汽车实际行驶中经历过上述过渡工况之后总得回到直线行驶状态上来,所以其中的ωr、β必然经历从接近零到峰值状态再到接近零的一个过程,在此取最大峰值点的数值来评价ωr、β对参数m,a,Iz变化的敏感程度。具体的灵敏度定义如下:
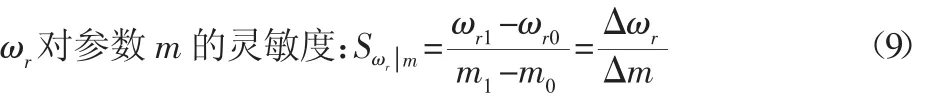
其他参数以此类推。
3.2 灵敏度定义的修正
考虑到ωr、β有着不同的量纲,按照(9)式计算灵敏度之后无法与Sβm进行横向的定量比较,故在此采用单因素扰动法,即在每次的扰动仅施加在一个参数上,而其他的参数保持真实值不变,以此来考察相对灵敏度的大小,故定义相对灵敏度如下:
ωr对参数m的相对灵敏度
式中:Δωri=ωri-ωr0(i=1,2,3);m0—当前汽车真实的整车质量;m1—加上一个扰动量Δm后含有误差的汽车整车质量;ωr0、ωr1—对应参数值 m0、m1为时通过 KF得到的 ωr估计值峰值。其他公式中符号定义以此类推。
通过上述分析及相对灵敏度的定义,将不同的状态量对不同参数的相对灵敏度可以放到同一平台下进行定量比较。大大简化其复杂的数学推导,同时可以有效的反应状态量对参数的敏感程度。
4 基于仿真试验的相对灵敏度分析
采用Carsim与Simulink联合仿真平台模拟典型过渡工况下的汽车操纵响应。鉴于稍后的实车试验中将采用普桑为试验车,所以为了保持试验一致性,仿真模拟中也采用普桑的整车参数进行建模,普桑整车的参数如下:m=1100kg,Iz=1720kg·m2,a=1.22m,b=1.28m,k1=-1.8×105N/rad,k2=-1.6×105N/rad,试验工况为双移线变道试验,试验车速为80km/h,采样时间为0.02s。仿真试验路径图,如图2所示。先按照真实参数进行对ωr、β滤波估计,然后分别给加上10%、20%、30%的误差扰动,则经过KF过程后,状态量的估计值分别,如图3、图4所示。同理给加上10%、20%、30%的误差扰动,按照上述步骤进行状态估计,在此不再将所有的对比图一一列出,仅将相对灵敏度的计算结果展示如下,如表1所示。通过计算所得的相对灵敏度结果:(1)横摆角速度和质心侧偏角对汽车质量的变化很敏感,不准确的整车质量将导致较大的估计结果误差;(2)而对的敏感度相对弱一些,对的敏感度最弱,基本上的变化不会引起横摆角速度和质心侧偏角的显著波动。(3)同时质心侧偏角对灵敏度的线性扰动呈现斜率递增的急剧增加趋势,说明的扰动误差对的估计精度具有决定其误差增长速度的作用。

图2 仿真试验路径Fig.2 Simulation Test Path
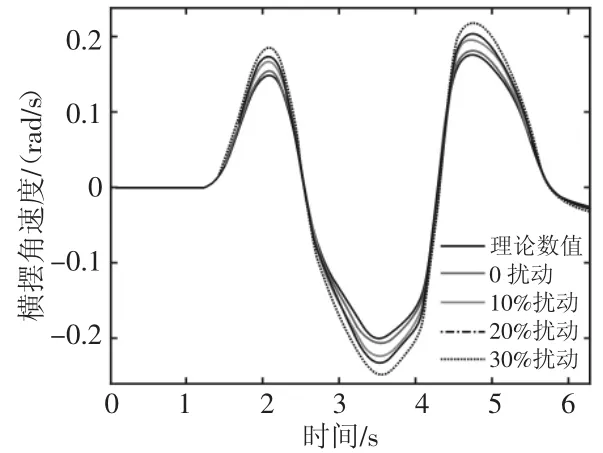
图3 不同m扰动量时ωr的估计Fig.3 Estimation ωrof Different m Disturbing Momentum

图4 不同m扰动量时β的估计Fig.4 Estimation β of Different m Disturbing Momentum

表1 仿真试验的相对灵敏度Tab.1 Relative Sensitivity of Simulation Test
5 基于实车试验的相对灵敏度分析
为从不同角度验证算法的有效性,实车试验将采取不同于仿真试验的双移线工况,在此采用另外一种工况进行实车试验,即蛇行绕桩试验。试验车辆为普桑,整车参数与第3节中相同,试验按照GB/T 6323.1-94严格进行。同理可得计算结果,如表2所示。从表2中我们可以得到与第3节相同的结论,具体不在重复,需要唯一强调的一点是,定义的相对灵敏度反映的是,汽车的结构参数对于基于KF滤波估计之后的汽车状态参数的精度影响,我们需要找出其中影响最大的参数,并采取相应算法对其进行控制。

表2 实车试验的相对灵敏度Tab.1 Relative Sensitivity of Real Vehicle Test
6 结论
基于单因素扰动法分析了汽车结构参数对汽车状态参数的影响,算法简单易行,并首次将汽车的结构参数对于基于KF滤波估计之后的汽车状态参数的精度影响进行量化研究,可以得出:(1)汽车横摆角速度和质心侧偏角对整车质量和质心至前轴的距离的相对灵敏度比较大,其中质心侧偏角对整车质量和质心至前轴的距离的相对灵敏度有随着扰动增加其表现为急剧恶化的趋势。(2)汽车横摆角速度和质心侧偏角对整车对z轴的转动惯量的相对灵敏度较小,相对于其他参数来说,该参数的扰动影响可以暂不考虑。通过上述结果分析,得出汽车状态估计的研究过程中应当注重对汽车整车质量和质心至前轴的距离两参数的自适应,这样可以增加不同工况下算法的鲁棒性,对汽车状态估计算法的研究起到很大的推动作用。
[1]赵又群.汽车动力学中若干关键状态和参数估计研究的现状与发展[J].中国机械工程,2010,21(10):1250-1253.(Zhao You-qun.Present state and perspectives of estimation research for several key states and parameters in vehicle dynamics[J].China Mechanical Engineering,2010,21(10):1250-1253.)
[2]余卓平,高晓杰.车辆行驶过程中的状态估计问题综述[J].机械工程学报,2009,45(5):20-33.(Yu Zhuo-ping,Gao Xiao-jie.Review of vehicle state estimation problem under driving situation[J].Chinese Journal of Mechanical Engineering,2009,45(5):20-33.)
[3]Wenzel T A,Burnham K J,Blundell M V.Dual extended kalman filter for vehicle state and parameter estimation[J].Vehicle System Dynamics,2006,44(2):153-171.
[4]郭孔辉,付皓,丁海涛.基于扩展卡尔曼滤波的汽车质心侧偏角估计[J].汽车技术,2009(4):1-3.(Guo Kong-hui,Fu Hao,Ding Hai-tao.Estimation of CG sideslip angle based on extended kalman filter[J].Automobile Technology,2009(4):1-3.)
[5]林棻,赵又群.基于双重扩展自适应卡尔曼滤波的汽车状态和参数估计[J].中国机械工程,2009,20(6):750-755.(Lin Fen,Zhao You-qun.Vehicle state and parameter estimation based on dual extended adaptive kalman filter[J].China Mechanical Engineering,2009,20(6):750-755.)
[6]Chen B C,Hsieh F C.Sideslip angle estimation sing extended kalman filter[J].Vehicle System Dynamics,2008(46):353-364.
[7]张义民,朱丽莎,王新刚.具有强非线性状态方程的机械零部件可靠性灵敏度分析方法[J].应用数学和力学,2010,31(10):1256-1266.(Zhang Yi-min,Zhu Li-sha,Wang Xinggang.Advanced method to estimate the reliability-based sensitivity of mechanical components with strongly nonlinear performance function[J].Applied Mathematics and Mechanics,2010,31(10):1256-1266.)
[8]Jiwon Oh,Seibum B.Choi.Design of a new composite observer for vehicle velocity and attitude estimation[C].Proceedings of the IASTED International Conference Control and Applications,Vancouver,BC,Canada,2011:102-109.

