基于干扰补偿的稳定平台控制系统设计
潘 帅,杨 奕,陈丹丹,朱海荣
(南通大学 电气工程学院,江苏 南通 226019)
1 引言
惯性稳定平台是一种利用光电传感器作为探测器件,能利用机电伺服系统隔离外界扰动,并且能自动识别并捕获目标,具有位置定位和伺服稳定两大功能的器件[1]。稳定平台的跟踪精度和稳定性能是惯性制导以及航天航空等领域发展的关键部分[2]。
高精度惯性稳定平台在低速运行状态下,受到非线性摩擦力矩、线缆力矩、耦合力矩等的影响,机械伺服转台会出现时走时停的“爬行”现象,稳定时有较大的静差或出现极限环振荡现象[3-5]。此外,当平台被应用于某些特殊的设备上时,平台的方位和俯仰框架也可能在运动过程中受到外界随机干扰力矩的影响(如风阻力矩或是飞鸟撞击等)。这些现象的存在使得伺服系统的跟踪精度和稳定性能大大降低。
目前,为了降低扰动力矩对伺服系统的影响,国内外学者作了大量的科研工作,文献[6-7]提出了基于LuGre摩擦模型的控制算法,从研究结果可以看出,这类方法有效地提高了系统了响应速度、减小了系统进入稳定状态的时间,同时在一定程度上也降低了误差,但是忽略了被控对象在遇到外界扰动时的影响,仅考虑了摩擦补偿问题。文献[8-10]针对所有影响被控对象的干扰因素提出了一种基于扰动观测器的扰动抑制设计方式,并取得了较好的控制效果,但是针对的实验对象是单轴伺服转台,忽略了多维运动时轴系间的耦合因素。因此,在总结前辈研究扰动补偿的基础上,对低速运行时转台遇到的扰动因素采用多重补偿的方式提出了一种基于动态摩擦模型的前馈补偿和基于扰动观测器反馈补偿的复合控制方案,并在某型号的稳定平台上进行实验验证,最终的实验结果表明,该控制策略能有效抑制摩擦及其它外部干扰力矩,有效地保证了稳定平台的跟踪精度和稳态性能。
2 带有摩擦的电机模型建立
由于两轴惯性稳定平台的方位轴和俯仰轴在不考虑外界干扰和轴系耦合的条件下,它们的控制系统可认为是相一致的,因此,在控制系统设计时以方位轴为例。根据电机的工作原理可得直流力矩电机的电压平衡方程式为:

式中:Ua—电枢电压;Ra、ia、La—电枢回路的电阻、电枢电流、电感;
e—电机反电动势,且:

式中:Ke—电机反电动势系数—转角速度。
根据电机电磁力矩和电流之间的关系可得电磁力矩Md的表达式:

式中:Km—电磁力矩系数。
在存在摩擦干扰的情形下,电机的转矩平衡方程式为:

式中:Mf—摩擦力矩;J—负载等效转动惯量。
LuGre动态摩擦模型是基于刚鬃的平均形变量z来建立的,z可表示为:

式中:σ1—微观阻尼系数;σ2—粘滞摩擦系数。
根据文献[5]提出的LuGre模型,模型各参数数值,如表1所示。

表1 LuGre模型参数值Tab.1 The Parameter Value of LuGre Model
由上述方程可得带摩擦的转台模型结构图,如图1所示。

图1 带摩擦转台模型框图Fig.1 The Turntable Model Diagram With Friction
3 复合控制策略的设计
3.1 基于摩擦模型的前馈补偿控制策略
以二轴惯性稳定平台方位轴为例,在综合以上模型的基础上,采用速度环(内环)和位置环(外环)双闭环控制系统,为减小机械摩擦对电机转速的影响,根据不变性原理,在内环增加前馈摩擦补偿控制。控制系统的模型框图,如图2所示。

图2 基于摩擦模型的前馈补偿框图Fig.2 The Feedforward Compensation Diagram Based on the Friction Model
传递函数;Kpwm—功率放大倍数;Kg—陀螺简化传递函数;
Mf1—摩擦估计值。
基于不变性原理,要使得前馈补偿环节传递函数和系统的闭环传递函数乘积始终为1。由于相对于比例系数而言,La、Ce和PI的积分系数比较小,忽略其影响,所以得关系式:
因此,只要能够辨识出LuGre摩擦模型中的各个参数值,就可以确定前馈补偿模型的各个系数值。

3.2 基于扰动观测器的力矩补偿控制策略
考虑轴系间的耦合问题后,将俯仰轴对方位轴的耦合影响视为俯仰轴对方位轴的扰动力矩干扰,再加上线缆力矩、风阻力矩等因素的影响,将图1中的电机、扰动、对象进行简化,如图3所示。

图3 带扰动电机简化结构Fig.3 The Simplified Structure of Motor with Disturbance

式中:d—外界干扰力矩。

即扰动力矩能够通过角加速度θ¨和电机电流i估算出来。角加速度通过陀螺仪反馈的角速度信号微分而得,由于测量过程中不可避免地会有噪声信号的干扰,因此需引入低通滤波器来抑制测量噪声信号。因此,扰动力矩的估计值为:

由式(11)可知扰动观测器的结构图,如图4所示。低通滤波器的参数τ的选择要结合系统的稳定裕度和对扰动的抑制能力两方面考虑。

图4 扰动观测器力矩补偿结构图Fig.4 The Torque Compensation Structure Based on Disturbance Observer
4 稳定平台单轴系统控制器设计
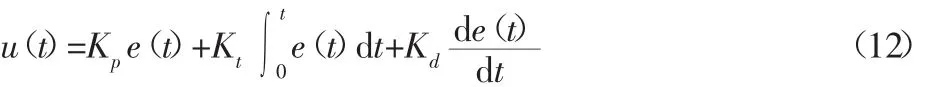
根据所建立的单轴转台模型,采用工程上最常用的PID算法,得到控制量:式中:Kp、Ki、Kd—PID 算法的比例、积分、微分系数;e(t)—转速误差。
4.1 位置环控制器设计
在实际系统的设计时,需要将式(12)进行离散化处理,位置环控制器采用的离散增量式PID算法,相应的增量式算式表示为:
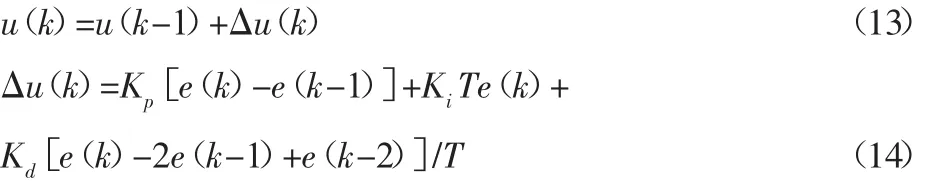
式中:T—系统的采样周期。
4.2 速度环控制器设计
类似于位置环控制器的设计,速度环采用的是抗积分饱和PI算法,其结构框图,如图5所示。

图5 抗积分饱和PI算法结构图Fig.5 The Diagram of Anti Integral Saturation PI Algorithm
图中:r(k)、u(k)—控制器的输入和输出;y(k)—反馈值;ω1—返回
常值;Umax、Umin—控制电压上下限。
根据图5可得:


其中,所以可以得到:
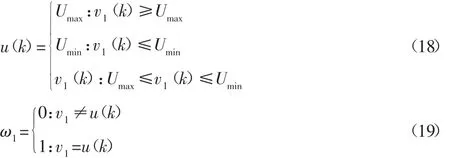
Kp、Ki、Kd、Kp1、Ki1的值先通过 MATLABsimulinkresponseoptimization工具箱得到,再在实验中进一步调整各参数值。
5 实验及结果
为验证提出的复合控制策略对摩擦以及其它力矩扰动的抑制性能,对其进行了实验论证,其中稳定平台的单轴系统原理框图,如图6所示。
根据系统模型的原理图,以及上述模型中的各参数的数值(Kf1=0.82,Kv=4,Kpwn=9.8),在 MATLAB/SIMULINK 模块中搭建仿真框图,在图5的仿真模型基础上调整PID、PI参数及前馈参数,保证系统有较好的响应状态。最终调得各参数值为:Kp=1400,Ki=0.03,Kd=0.01,Kp1=13800,Ki1=0.01。
当给定幅值为1的阶跃信号时,根据仿真图7可以得知,常规控制下,系统受外界干扰影响较大,调节时间较长,约为0.1s,在控制系统引入复合控制时,系统响应时间减小到0.06s,因此仿真结果可表明复合控制能有效抑制影响稳定平台的干扰因素。

图7 有无复合控制时阶跃响应仿真图Fig.7 The Simulation Diagram of Step Response with Presence of Compound Control
针对某型号的惯性稳定实验平台,采用提出的控制策略进行实验验证,由于主要针对速度内环进行优化设计,所以首先对速度环进行验证,给速度输入指令分别输入不同速度值。从图8中可以看出,系统在高速和低速运行时都具有较快的响应,且速度抖动幅值很低。

图8 速度环速度响应曲线Fig.8 Velocity Response Curve of the Speed Loop

图9 有无复合控制时稳定状态下速度误差比较图Fig.9 Velocity Error Comparison Chart on Steady State with Presence of Compound Control
从图9中可以看出复合控制下,两轴稳定平台的单轴转台在低速运行时,当系统处于稳定状态时,速度误差减小为常规控制下速度误差的50%左右。
加入位置环后,在双闭环控制的系统中,对位置输入指令赋值,当给定位置指令信号为幅值为(±5)°的正弦信号时,响应如图7,此时的位置误差值与常规控制方式的误差值比较图,如图10所示。

图10 双闭环复合控制下位置跟踪曲线Fig.10 Location Tracking Curve with Compound Control Under the Double Closed Loop

图11 有无复合控制时位置误差比较图Fig.11 The Comparison Chart of Position Error with Presence of Compound Control
从图10和图11中可以看出,引入复合控制方法后,系统具有了良好的跟踪性能,位置跟踪误差也降至常规控制方式的40%左右。
6 结论
优化了一种两轴的惯性稳定平台的控制系统,针对双闭环系统中的速度环提出了一些改进意见。首先针对机械摩擦及其它外界扰动力矩导致的电控系统中电机转动惯量发生变化问题,建立基于LuGre动态摩擦模型的转台模型,并对此提出了一种摩擦前馈补偿和扰动观测器反馈补偿的复合控制策略,对摩擦及其它外界扰动起到了很好的抑制作用,极大地减小了系统低速时抖动、爬行现象,同时也提高了惯性稳定平台的跟踪精度,降低了跟踪误差。
惯性稳定平台在诸多领域都有实用性,研究的是两轴的惯性稳定平台,主要考虑的是机械摩擦、外界扰动力矩和轴系耦合的影响,还有例如陀螺仪的零漂、时滞补偿等问题都是未来研究的一个方向。
[1]张新勇,王合龙,刘昇.机载光电稳定平台的模型辨识研究[J].电光与控制,2014,21(3):62-71.(Zhang Xin-yong,Wang He-long,Liu Sheng.The research of model identification on airborne photoelectric stabilized platform[J].Electronics Optics&Control,2014,21(3):62-71.)
[2]Hilkert J M.Inertially stabilized platform technology concepts and principles[J].IEEE Control Systems Magazine,2008,28(1):26-46.
[3]任彦,刘正华.滑模自适应控制在光电稳定平台中的应用[J].控制工程,2014,21(1):32-40.(Ren Yan,Liu Zheng-hua.The application of sliding model adaptive control in the photoelectric stabilized platform[J].Control Engineering,2014,21(1):32-40.)
[4]王毅,何联.伺服系统的摩擦补偿[J].电机与控制学报,2013,17(8):107-112.(Wang Yi,He Lian.The friction compensation of servo system[J].Electric Machines And Control,2013,17(8):107-112.)
[5]孔祥臻,王勇,蒋守勇.基于Stribeck模型的摩擦颤振补偿[J].机械工程学报,2010,46(5):68-73.(Kong Xiang-xi,Wang Rong,Jiang Shou-yong.The compensation of friction flutter based on the stribeck model[J].Journal of Mechanical Engineering,2010,46(5):68-73.)
[6]Canudas Dew IT C,Olsson H,Astrom K J.A new model for control of systems with friction[J].IEEE Trans on Automatic Control,1995,40(3):419-424.
[7]丛中旖.基于LuGre模型的伺服转台自适应反演滑模控制[J].四川兵工学报,2014,35(7):75-78.(Cong Zhong-yi.The adaptive inversion sliding mode control of servo turntable based on LuGre model[J].Journal of Sichuan Ordnance,2014,35(7):75-78.)
[8]Giuseppe Fedele,Member,IEEE,and Andrea Ferrise.Biased Sinusoidal Disturbance Compensation With Unknown Frequency[J].IEEE Transactions on Automatic Control,2013,58(12):3207-3212.
[9]ZhongYi Chu,Member,IEEE,Jing Cui,and FuChun Sun.Fuzzy Adaptive Disturbance-Observer-Based Robust Tracking Control of Electrically Driven Free-Floating Space Manipulator[J].IEEE Systems Journal,2014,8(2):343-352.
[10]Edomir Milosavljevi,Branislava Perunii-Draenovi,Boban Veseli.Discrete-Time VelocityServo System Design Using Sliding Mode Control Approach With Disturbance Compensation[J].IEEE Transactons on Industrial Informatics,2013,9(2):920-927.

