下肢康复训练机器人髋关节机构的振动分析

洪跃镇 ，隋建锋 ，赵成坚 ，季林红

（1.清华大学 摩擦学国家重点实验室智能与生物机械分室，北京 100084；2.中国航天员科研训练中心人因工程重点实验室，北京 100094）

1 引言

大多数脑卒中患者有不同程度的生活能力和劳动能力的丧失，国内外多数学者提倡脑卒中后应当早期进行康复训练，已有研究和临床实验表明早期的康复治疗可以时此类患者恢复大部分运动功能[1]。目前对于脑卒中等中枢神经损伤患者通常采用治疗师一对一的手法治疗，效率低、强度大，市场上比较缺少适用于脑卒中早期康复治疗的下肢康复训练机器人[2]。清华大学康复工程研究中心设计了一种的下肢康复训练机器人，用于脑卒中早期下肢康复训练，实现下肢腿部肌肉力量训练和大脑运动皮质区刺激作用。

目前，机械振动分析方法的运用和研究很多[3-5]，相关结论对机电产品的状态设置、故障诊断等具有重要意义[6-8]。以康复机器人对患者进行被动节律性训练为工作状态，利用振动力学模型研究康复机器人髋关节机构的运动特点和振动性能，以指导康复机器人节律性机构的工作频率的设计和后续对振动的主动控制，避免工作频率和康复机器人部件发生共振，并使得患者的舒适度和康复效果达到最佳，助于避免康复设备的工作时对患者肌肉、骨骼或神经造成的二次伤害，增强康复训练的针对性和科学性。

2 髋关节机构工作分析

康复训练机器人由髋关节机构、足底机构、扰动机构、倾斜机构和控制系统5部分组成。其训练原理是：患者患病初期无法站立，将康复装置和直立床相结合，通过电动推杆实现床体角度的变化，实现患者姿态的改变；采用床板上的凹槽和支撑的方式相结合实现患者减重，下肢训练设备通过髋关节和踝关节机构动作组合，满足不同康复时期的训练任务，实现患者的被动、主动、阻尼等多种模式的运动形式，通过节律性训练和非节律性刺激配合实现康复训练。

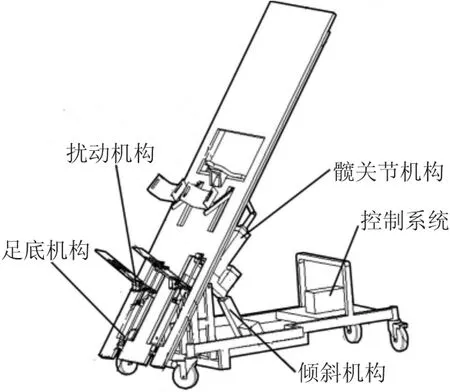
图1 康复训练机器人示意图Fig.1 The Rehabilitation Robot

机器人在工作时对人体产生的振动分为两类：其一是由电机不平衡惯性力及力矩引起的高频（一般在20Hz以上）简谐振动和振动噪声，其二是电推杆往复运动引起的低频（10Hz以下）振动。相比于高频振动，低频振动对人体的影响更大。并且通过电机型号、功率的选择及降低机构之间的摩擦力等措施，可以较好的降低高频振动和振动噪声。

在康复训练机器人进行被动节律性训练模式下，振动源主要是下肢训练装置，具体是髋关节机构。髋关节结构的执行机构是L形杆件，L形杆件为成直角固结在一起的两段铝杆组成，与电推杆滑块接触的称为动力杆，与人体大腿接触的称为接触杆，接触杆和固定于其上的大腿托座组成接触部件。

髋关节机构工作时，电推杆铰接在床板架上，另一端通过销钉与L形杆件铰接，同时L形杆件通过旋转轴与床板架铰接，组成曲柄滑块机构，电推杆的伸缩带动L形杆件绕旋转轴转动，从而带动患者髋关节的屈曲和伸展，L形杆件上固定直线导轨，直线导轨的滑块上固定大腿支撑架，患者的大腿通过柔性绑带固定到大腿支撑架上，直线导轨的滑动可以适应不同患者不同的大腿长度；踝关节机构电动驱动通过一对锥齿轮驱动丝杠实现直线往复运动，如图1所示。

3 振动学模型的建立

不同支承条件下梁的振动可以用频率方程进行动力分析与动态设计。从以上工作原理分析，如图2所示。髋关节机构是电机转动带动丝杠直线往复运动，丝杠直线往复通过曲柄滑块机构变成L形杆件绕旋转轴转动。将髋关节机构看作一个基础作简谐运动的单自由度阻尼系统。以L形杆件转角φ为广义坐标，从工作原理到机构运动（直线往复、绕旋转轴转动），再到振动点广义坐标的变化（L形杆件转角φ），逐步推进建立振动学模型。

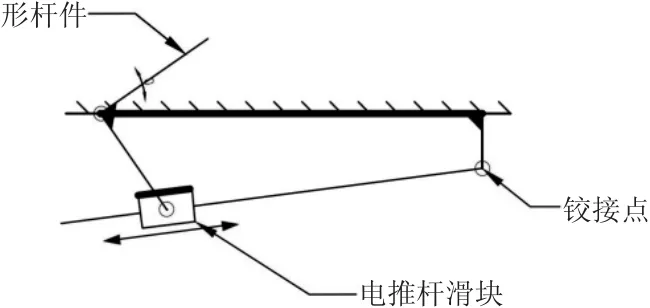
图2 髋关节机构机械原理示意Fig.2 The Mechanical Principle of Hip Training Part

假设电推杆的运动方程为xs=asinωt。L形杆件与滑块及床板通过铰接接触，L形杆件本身的变形、接触部位存在的摩擦等因素导致刚度和阻尼的存在，将滑块与杆铰接产生的刚度和杆与床身铰接产生的刚度合并等效为刚度k，将滑块与杆铰接产生的阻尼和杆与床身铰接产生的阻尼合并等效为阻尼c。将接触杆本身质量及接触杆端点质量等效到L形杆件的与人体大腿接触杆的端点，等效质量假设为m。髋关节机构理论模型，如图3所示。

以L形杆件转角φ为广义坐标，由系统的动量矩定理：

康复训练机器人在稳定工作状态下，基础作简谐运动的单自由度阻尼系统的响应频率与激振频率一样，假设在接触杆的角度振动方程为 φ（t）=Bφsin（ωt-φ），在接触杆的端点（等效质量点）的位移振动方程 L（t）＝φ（t）L＝BLsin（ωt-φ）。

根据振动理论相关公式[9]，角位移传递率为：

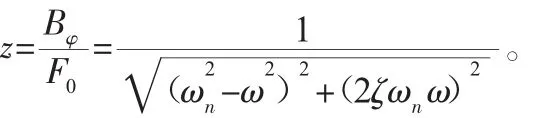
得到L形杆件的角位移振幅为：

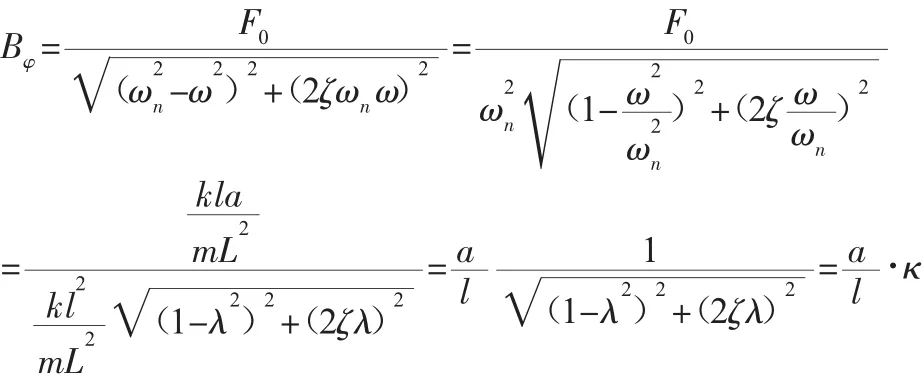
同理，根据振动理论相关公式，电推杆运动与L形杆件摆动相位差的正切值

故接触杆的角度振动方程为：

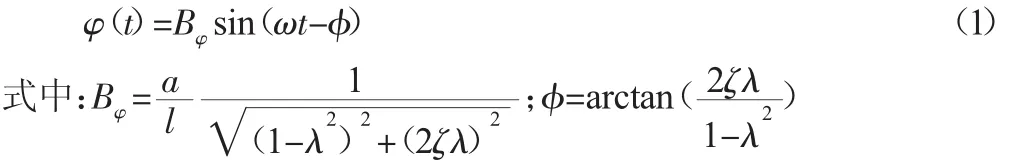
故接触杆的端点的位移振动方程为：

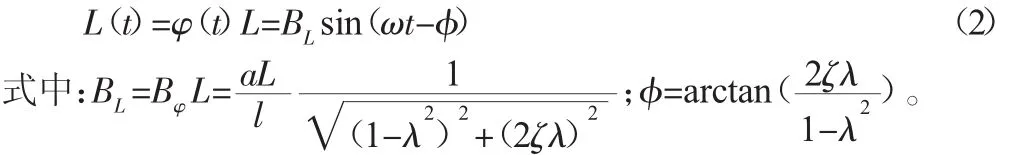
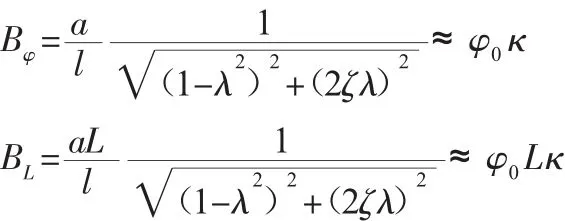
分析髋关节训练机构的执行部件L形杆件的角位移和位移振幅表达式，当丝杠ω=0时≈φ，0定义表达式中共同变量κ=为振幅影响系数，它是频率比和阻尼比的函数，下面分析不同频率比和阻尼比对影响系数和相位差的影响。

4 分析与讨论

4.1 频率比、阻尼比与振幅影响系数

不同的阻尼比、频率比与角位移振幅影响系数的关系曲线，如图4所示。

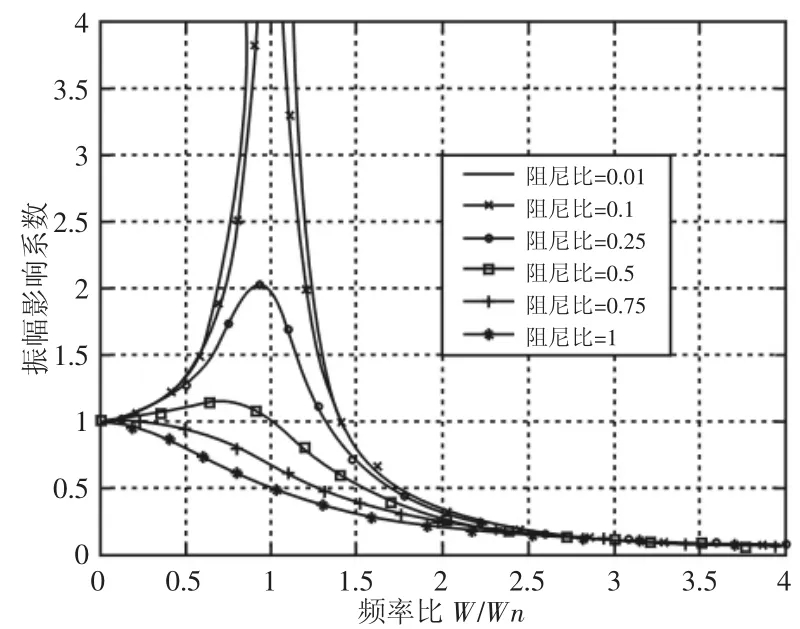
图4 振幅影响系数变化曲线Fig.4 The Curve of Characteristics of the Amplitude

讨论：

4.2 频率比、阻尼比与相位差

不同的阻尼比、频率比与相位差的关系曲线，如图5所示。

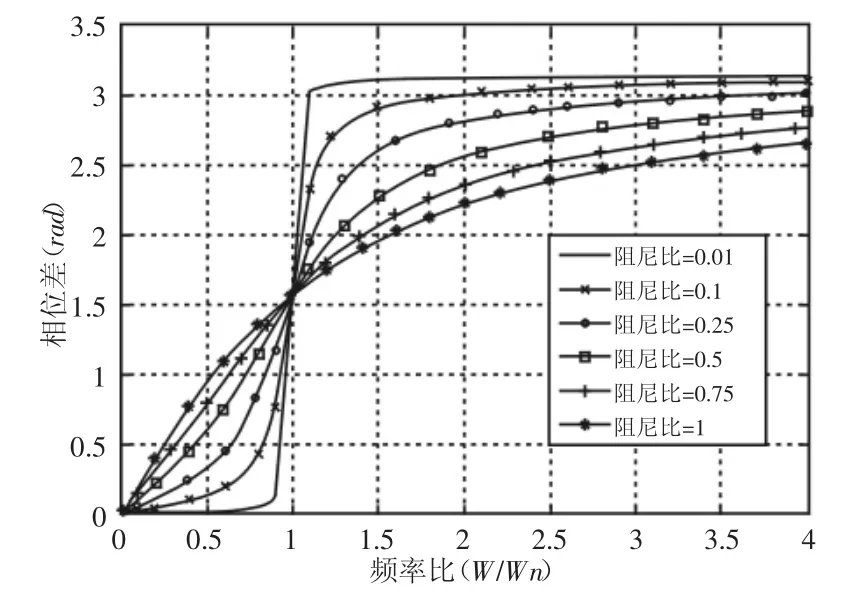
图5 相位差变化曲线Fig.5 The Curve of Characteristics of the Phase

讨论：

（1）由于阻尼的存在，导致执行杆件的运动与电推杆滑块的运动之间产生延时，存在相位差，相位差仅和阻尼比和频率比有关。

（2）相位差受频率比的影响较大。当阻尼比很小时（约0.01），在低频范围内，相位差接近于0，即响应与激励接近于同相位；在高频范围内，相应与激励接近于反相。

5 结论

（1）康复训练机器人髋关节机构的固有频率与机构等效质量、等效刚度、执行杆件长度，考虑到杆件的刚度较大，固有频率会很大。康复机器人髋关节机构设计要尽量使得摩擦阻尼很小，此时末端振幅比仅是频率比的函数。

（3）机构存在一个临界阻尼，超过临界阻尼后，不管工作频率怎么设置，振幅都小于静变形。而在小阻尼情况下，才会发生共振，阻尼的存在显著降低共振位移振幅。

（4）当要利用机器人髋关节机构的振动进行振动康复训练时，应该尽量降低阻尼，并使工作频率接近固有频率。反之欲减小振动，则要增大阻尼，并使工作频率远离固有频率。

（5）由于阻尼的存在，执行杆件的运动与电推杆滑块的运动幅度并不是同时达到最大，存在相位差。当在低频范围内，相位差接近于0，即响应与激励接近于同相位；在高频范围内，相应与激励接近于反相。

考虑环境及设备振动的影响，研究人体在振动环境下的动力特性并对人体舒适度进行合理评价，相关研究结果表明，人能承受的全身振动的最低频率是（4～8）Hz，部分身体的振动在某一频率范围内会对身体某些部位产生局部损害，人体躯干不同部位具有不同的敏感振动频率[10]，因此在设置工作频率时应该避开人体敏感频率。

探讨了康复机器人髋关节机构振动学特性，对设置机器人机构的工作频率和和对振动进行主动控制提供了理论依据，也对完善人体舒适度评价方法和减小振动对人体的危害提供了参考。

［1］杨红专.脑卒中的康复治疗进展［J］.中外医疗，2011（2）：182-184.（Yang Hong-zhuan.The development of rehabilitation therapy after stroke［J］.China Foreign Medical Treatment，2011（2）：182-184.）

［2］张琳瑛.脑卒中康复治疗技术的研究进展与应用［J］.中国临床康复，2004，8（4）：7768-7769.（Zhang Lin-ying.Research progress and application of treatment technique for stroke rehabilitation［J］.Chinese Journal of Clinical Rehabilitation，2004，8（4）：7768-7769.）

［3］刘宗政，陈恳，陈振华.滚动轴承的振动特性分析及典型故障诊断［J］.机械设计与制造，2009（3）：103-105.（Liu Zong-zheng，Chen Ken，Chen Zhen-hua.Measure and analysis about vibration characteristic of roller bearing fault［J］.Machinery Design ＆Manufacture，2009（3）：103-105.）

［4］Lawrence A.Hawkins，Rasish K.Khatri，Koman B.Nambiar.Test results and analytical predictions for MIL-STD-167 vibration testing of a direct drive compressor supported on magnetic bearings［J］.Journal of Engineering for Gas Turbines and Power.2015，137（5）：052501-052508.

［5］Jihyun Lee，Chinedum Okwudire.Effects of non-proportional damping on the residual vibrations of mode-coupled ultra-precision manufacturing machines.proceedings of the ASME 2014 dynamic systems and control conference［C］，2014，San Antonio，USA.

［6］聂松辉，李鸿，颜彧.摆线钢球减速器振动分析［J］.机械设计与研究，2014，30（2）：56-58，64.（Nie Song-hui，Li Hong，Yan Yu.The vibration analysis of the cycloid steel ball reducer［J］.Machine Design and Research，2014，30（2）：56-58，64.）

［7］郑鹏.机床加工过程振动特性及对加工表面质量影响的研究［D］.武汉：华中科技大学，2012.（Zheng Peng.Research on vibration characteristics in machining processing and the affect of machined surface quality［D］.Wuhan：Master Dissertation of Huazhong University of Science and Technology.2012.）

［8］任尊松，刘志明.高速动车组振动传递及频率分布规律［J］.机械工程学报，2013，49（16）：1-7.（Ren Zun-song，Liu Zhi-ming.Vibration and frequency domain characteristics of high speed EMU［J］.Journal of Mechanical Engineering，2013，49（16）：1-7.）

［9］张义民.机械振动［M］.北京：清华大学出版社，2007.（Zhang Yi-min.Mechanical Vibration［M］.Beijing：Tsinghua University Press，2007.）

［10］Singiresu S.Rao著.李欣业，张明路 译.机械振动（第 4版）［M］.北京：清华大学出版社，2009.（Singiresu S.Rao.Li Xin-ye，Zhang Ming-lu trans.Mechanical Vibrations（Four Edition）［M］.Beijing：Tsinghua University Press，2009.）