振动信号模型在滚动轴承故障诊断中的应用

郭艳平，龙涛元

（中山火炬职业技术学院，广东 中山 528436）

1 引言

滚动轴承是风力发电机组等旋转机械的重要传动部件，齿轮箱是风力发电机组中最易发生故障的部件[1]，由于其处于一百多米的高空，所以齿轮箱的维护或更换费时费力，因此，对风电机组齿轮箱中的滚动轴承和齿轮等旋转机械的故障诊断方法进行研究具有重要的理论、经济和实际应用价值。

目前已有很多先进的信号分析方法被应用在轴承故障诊断中，例如傅里叶变换、窗口傅里叶变换、Wigner-Ville分布和小波分析等，但上述几种方法均有其局限性，不适合用于分析振动等非平稳信号，EMD是一种自适应的时频分析方法，分解可获得若干个具有一定物理意义的IMF（intrinsic mode function）分量，它非常适合对非平稳、非线性的信号进行分析，所以在旋转机械故障诊断领域有广泛且有效的应用。

诊断流程的第二步是故障特征提取，常用有量纲时域特征量包括：最大值、均值、方差、均方幅值等，无量纲时域特征量包括：峭度，波形指标，峰值指标，脉冲指标，裕度指标等[4]，这些特征量各有其使用场合，但很难兼顾敏感性和稳定性，例如峰值因子、峭度在故障发生的早期阶段较敏感，但稳定性不够，当故障发展到严重阶段时，这两个特征值和正常状态时相同。文献[5]提取的故障特征参数是经EMD分解后所得各个IMF的能量，该特征参数易受信号传播路径和传感器参数的影响，具有不稳定性；文献[6]提取包络谱中特征频率处的幅值比作为故障特征量，该指标也具有很大的波动性。诊断流程的第三步是模式识别，即利用提取的故障特征量输入模式识别算法，从而实现故障诊断和决策，这一步骤中常用的神经网络[5]、支持向量机[6]等识别算法往往需要大量的典型故障训练样本，而实际应用中很难采集到有典型故障特征的大量样本。文献[7]中采用的支持向量机虽然不需要大量样本，但同样需要小样本来支撑，才能实现滚动轴承故障的正确诊断。

针对上述分析，提出一种基于EMD和振动信号模型的滚动轴承故障诊断方法，该方法不需要提取故障特征量，也不需要大量典型故障样本作为支撑，通过对实验平台信号和风电场现场信号的分析结果验证了其有效性和实际应用价值。

2 滚动轴承振动信号模型

2.1 正常状态

当轴承处于正常运行状态时，轴以一定的速度旋转，此时的振动主要由轴承结构特点造成的承载刚度变化引起，其主要成分为轴的旋转频率分量，信号模型可表示为：

式中：x（t）—时域信号；xm—第m阶转动频率谐波分量的幅值；φm—第m阶转动频率谐波分量的相位；fn—轴的转动频率。

2.2 外圈存在单个损伤点的状态

当轴承的外圈上存在单个损伤点时，随着轴的旋转，损伤点与滚动体周期性的接触产生一系列脉冲力，脉冲间隔时间为1/fo，fo为外圈故障特征频率，频谱特征表现为：一系列以外圈故障特征频率为间隔，幅值随频率的增大而逐渐减小的离散谱线，所以外圈存在单个损伤点的信号模型可表示为：

式中：x（t）—时域信号；xm—第m阶谐波分量的幅值；φm—第m阶

谐波分量的相位；fo—外圈故障特征频率。

2.3 内圈存在单个损伤点的状态

当内圈上存在单个损伤点时，损伤点随轴一起转动，并与滚动体周期性接触，从而产生一系列脉冲，频谱特征表现为：形成以内圈故障特征频率及其倍频为中心，以轴的旋转频率及其倍频为调制频率的调制边频带；各阶中心频率的幅值随频率增大而逐渐下降；调制频率的幅值在远离各阶中心频率时逐渐下降。所以内圈存在单个损伤点的信号模型可表示为：

式中：x（t）—时域信号；xm—第m阶谐波分量的幅值；φm—第m阶谐波分量的相位；Am，n—调制函数的第 n阶分量的幅值；αm，n—调制函数的第n阶分量的相位；fi—内圈故障特征频率；fn—轴的转动频率。

2.4 单个滚动体存在单个损伤点的状态

当单个滚动体上存在单个损伤点时，滚动体上的损伤点与外圈和内圈周期性的接触，从而产生一系列大小和方向受载荷分布和损伤点位置影响的脉冲，频谱特征表现为：以滚动体故障特征频率为间隔，幅值随频率的增大而逐渐减小的离散谱线，所以滚动体存在单个损伤点的信号模型可表示为：

式中：x（t）—时域信号；xm—第m阶谐波分量的幅值；φm—第m阶谐波分量的相位；fr—滚动体故障特征频率。

3 滚动轴承故障诊断方法

3.1 原始振动信号去噪

EMD非常适合对轴承振动信号之类的非平稳、非线性信号进行分析，EMD可认为是一组自适应的高通滤波器，经过滤波过程，可得到一系列频率成分和带宽随信号的变化而变化的IMF分量，这些分量具有调制特征。所以应用EMD将原始振动信号分解为若干个具有一定物理意义的包含冲击脉冲调制等故障信息的IMF分量，然后以峭度[8]大于3为依据进行信号重构，之所以选取峭度作为衡量指标，主要是考虑到该指标对冲击脉冲成分特别敏感，同时与轴承的转速、尺寸、载荷等因素无关。通过此种信号处理过程，可将干扰噪声去除，同时突显冲击脉冲和调制等故障信息，为下一步的故障诊断奠定良好的基础。

3.2 故障特征频率

滚动轴承带损伤点旋转时，损伤点会与其它零部件周期性的接触，并产生冲击激振力，这些激振力发生的频率称为故障特征频率，滚动轴承的外圈、内圈和滚动体的故障特征频率计算公式依次为：

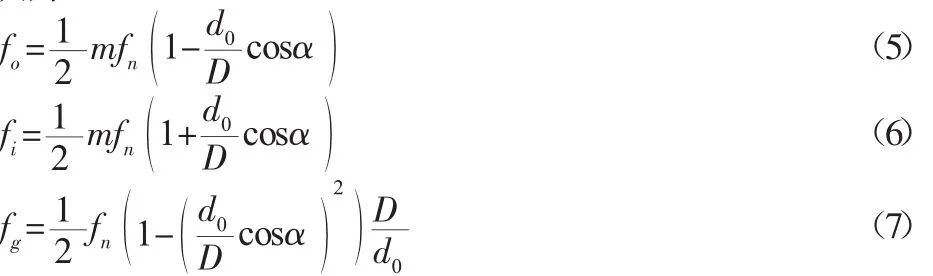
式中：fn—轴的转动频率；m—滚动体的个数；d0（mm）—滚动体的直径；D（mm）—滚动轴承的节径；α（°）—接触角。

3.3 故障诊断方法流程

基于EMD和振动信号模型的滚动轴承故障诊断方法步骤如下：（1）按照一定的采样频率采集原始振动信号；（2）对振动信号样本进行EMD分解，可得到若干个IMF分量，以峭度大于3为依据进行信号重构；（3）计算滚动轴承内圈、外圈、滚动体的故障特征频率，并依次建立轴承在正常、外圈存在单个损伤点、内圈存在单个损伤点、滚动体存在单个损伤点四种状态下的振动信号模型；（4）依次计算重构信号和四个典型信号模型之间的相关系数；（5）根据相关系数大小判断轴承状态。

4 实验信号分析

为验证故障诊断方法的有效性，下面对实验平台采集的信号进行分析，该实验平台来自美国Case Western Reserve University电气工程实验室的滚动轴承故障试验台[9]，随机选取外圈存在故障点的样本130.mat进行分析，采用EMD对样本进行分解，得到10个IMF分量和一个剩余分量，为了衡量每个IMF分量所包含冲击脉冲及调制等故障信息的多少，特计算每个IMF的峭度依次为［5.22，8.19，5.83，3.45，3.19，3.76，3.63，2.93，2.38，2.27］，用峭度值大于3的前7个分量重构信号，即f′=IMF1+IMF2+IMF3+IMF4+IMF5+IMF6+IMF7，如图1所示，该重构信号f包含周期性的冲击脉冲成分，并具有明显的调制特征。

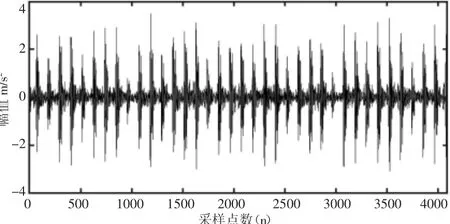
图1 重构信号时域波形图Fig.1 The Time-domain Waveform of The Reconstructed Signal

下面进行故障诊断流程的第三步，即建立轴承振动信号模型，首先计算各零部件的故障特征频率：轴的转动速度为1797rpm；轴的转频fn=29.95Hz；内圈故障特征频率为fi=5.4152fn=162Hz；外圈故障特征频率为fo=3.5848fn=107Hz；滚动体故障特征频率为fr=4.7135fn=141Hz。考虑到经过EMD方法“带通滤波”后，一些高倍频谐波会被抑制，所以令各阶倍频均取到3倍频，频率调制取一阶调制，同时令相位为零，可得滚动轴承振动信号模型。

正常状态下的振动信号模型1：

Asin（2πfnt）+A/2sin（2π2fnt）+A/4sin（2π3fnt）

外圈存在单个损伤点的信号模型2：

Asin（2πfot）+A/2sin（2π2fot）+A/4sin（2π3fot）

内圈存在单个损伤点的信号模型3：

Asin（2πfit）+A/2sin（2π2fit）+A/4sin（2π3fit）+A/2sin（2π（fifn）t）+A/2sin（2π（fi+fn）t）+A/4sin（2π（2fi-fn）t）+A/4sin（2π（2fi+fn）t）+A/8sin（2π（3fi-fn）t）+A/8sin（2π（3fi+fn）t）

滚动体存在单个损伤点的信号模型4：

Asin（2πfrt）+A/2sin（2π2frt）+A/4sin（2π3frt）

上述模型中A的取值为待测样本经EMD分解后所得重构信号的峰值，即待测样本130.mat的重构信号峰值3.5m/s2，所以A=3.5。依次计算重构信号与各信号模型之间的相关系数，结果分别为：0.0007；0.0257；0.0054；0.0017。

5 现场信号分析

为验证所提出故障诊断方法的有效性和实际应用价值，特对某公司在张家口市满井风电场1.5MW风电机组上采集的振动数据进行分析[10]，2010年7月在线监测到齿轮箱高速端径向加速度传感器所拾取的振动幅值明显增大，该轴承型号为NJ 2326E，计算内圈故障特征频率为fi=8.3fn；外圈故障特征频率为fo=5.6fn；滚动体故障特征频率为fr=4.9fn，fn为轴的旋转频率。风力发电机组齿轮箱高速端振动加速度传感器测点布置图，如图2所示。首先采用EMD对待测样本进行分解，结果得10个IMF分量，其中前四个分量的峭度值大于3，遂进行信号重构，即f（t）=IMF1+IMF2+IMF3+IMF4，然后依次建立该轴承在正常、外圈存在单损伤点、内圈存在单损伤点和滚动体存在单损伤点四种情况下的振动信号模型，并计算重构信号与这四个信号模型之间的相关系数，结果依次为：0.0035；0.0298；0.0146；0.0022，由此可判断轴承故障点位于外圈上，服务人员更换轴承时发现外圈严重剥落，且润滑油被金属颗粒污染严重，更换轴承后的振动幅值明显变小，如图3所示。

图2 风力发电机组齿轮箱测点布置图Fig.2 The Layout of Acceleration Sensor for Wind Turbine Gearbox

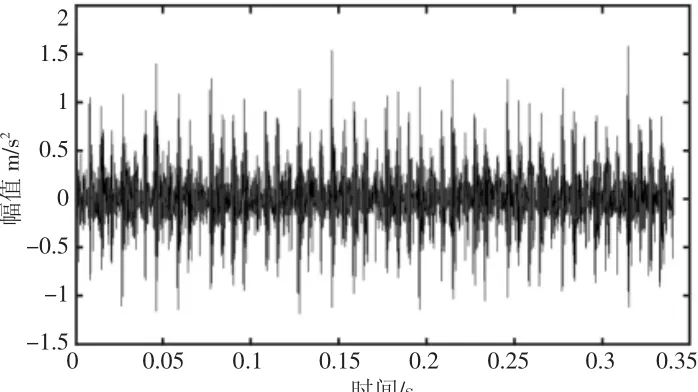
图3 待测样本波形图Fig.3 The Waveform of Sample

6 结论

提出一种基于EMD和振动信号模型的滚动轴承故障诊断方法，该方法首先采用EMD将原始振动信号分解为若干个IMF分量，并以峭度大于3为依据进行信号重构，以便去除包含在原始信号中的噪声，更进一步突显冲击脉冲调制等故障信息，然后在建立轴承在正常、外圈单点损伤、内圈单点损伤、滚动体单点损伤四种情况下信号模型的基础上，计算重构信号与这四种模型之间的相关系数，最后根据相关系数可判断故障点所在部位，通过对仿真实验平台信号的分析，证明了该方法的有效性，进一步将其应用在风力发电机组齿轮箱高速端滚动轴承振动加速度信号的分析中，验证了故障诊断方法的有效性和实用性。和常规故障诊断流程作对比，所提出方法的优点包括：（1）不必统计时域或频域的故障特征量，而是直接以故障特征频率为参考值，并建立了轴承在各种典型情况下的振动信号模型。（2）不需要大量典型故障样本，即使只有一个待测故障样本也可实现故障的正确诊断。

［1］JOHAN R，LINA M B.Survey of failures in wind power systems with focus on Swedish wind power plants during 1997-2005［J］.IEEE Transaction on Energy Conversion，2007，22（1）：167-173.

［2］丁康，李巍华，朱小勇.齿轮及齿轮箱故障诊断实用技术［M］.北京：机械工业出版社，2006：64-65.（DingKang，Li Wei-hua，ZhuXiao-yong.Practical technology for fault diagnosis of gear and gearbox［M］.Beijing：Machinery Industry Press，2006：64-65.）

［3］梅宏斌.滚动轴承振动监测与诊断［M］.北京：机械工业出版社，1995：17-26（Mei Hong-bin.Vibration monitoring and diagnosis of rolling bearing［M］.Beijing：Machinery Industry Press，1995：17-26.）

［4］任学平，吴剑，庞震.基于复合信号处理的滚动轴承早期微故障诊断研究［J］.机械设计与制造，2015（5）：147-149.（Ren Xue-ping，Wu Jian，Pang Zhen.Research on weak signal detection technology of rolling bearing early fault based on composite signal processing［J］.Machinery Design and Manufacture，2015（5）：147-149.）

［5］杨宇，于德介，程军圣.基于EMD与神经网络的滚动轴承故障诊断方法［J］.振动与冲击，2005，24（1）：85-88.（Yang Yu，Yu De-jie，Cheng Jun-sheng.Roller bearing fault diagnosis methodbasedonEMDandneuralnetwork［J］.JournalofVibrationandShock，2005，24（1）：85-88.）

［6］程军圣，于德介，杨宇.基于SVM和EMD包络谱的滚动轴承故障诊断方法［J］.系统工程理论与实践，2005，25（9）：131-136.（Cheng Jun-sheng，Yu De-jie，Yang Yu.A Fault diagnosis approach for roller bearing based on SVM and EMD envelope spectrum［J］.Systems Engineering-Theory and Practice，2005，25（9）：131-136.）

［7］Meng L，Miao W，Wang C.Research on SVM classification performance in rolling bearing diagnosis［C］.International Conference on Intelligent Computation Technology and Automation.IEEE Computer Society，2010：132-135.

［8］胡爱军，马万里，唐贵基.基于集成经验模态分解和峭度准则的滚动轴承故障特征提取方法［J］.中国电机工程学报，2012，32（11）：106-111.（Hu Ai-jun，Ma Wan-li，Tang Gui-ji.Rolling bearing fault feature extraction method based on ensemble empirical mode decomposition and kurtosis criterion［J］.Proceedings of the CSEE，2012，32（11）：106-111.）

［9］The case western reserve university bearing data center［EB/OL］.2012（11）.

［10］郭艳平，颜文俊，包哲静.风力发电机组在线故障预警与诊断一体化系统设计与应用［J］.电力系统自动化，2010，34（16）：83-86.（Guo Yan-ping，Yan Wen-jun，Bao Zhe-jing.Design and application of online fault warning and diagnosis integrated system for wind turbines［J］.Automation of Electric Power Systems，2010，34（16）：83-86.）