薄煤层工作面巡检机器人越障前动力学分析

商德勇，杨 壘，杜少庆，范 迅

（中国矿业大学（北京）机电与信息工程学院，北京 100083）

1 引言

我国薄煤层资源储量丰富，分布广泛，已经实现了综合机械化、自动化开采，但是由于薄煤层工作面空间狭窄，使得设备维护检修比较困难。四摇臂履带式薄煤层综采工作面巡检机器人可以辅助或代替工人完成日常巡检工作，减轻了采煤工作面检修工人的劳动强度[1-2]。对四摇臂履带式结构的机器人在越障过程中的动力学过程进行分析，可以分析越障过程中驱动电机输出转矩的变化规律，为电机的合理选型提供理论依据。相关文献[3-10]对四摇臂结构的机器人在自撑起状态下和越障过程中的动力学进行了分析，但未对越障前的过程进行分析。对四摇臂履带式机器人越障前过程进行了动力学分析，有助于提高巡检机器人的越障性能。

2 巡检机器人行走机构结构

薄煤层综采工作面地形环境多变，要求巡检机器人具有较强的越障能力和行驶能力，通过对不同结构类型机器人特性分析，采用四摇臂式履带结构作为巡检机器人行走机构的结构方案。巡检机器人行走部结构，如图1所示。

图1 巡检机器人行走机构样机Fig.1 The Walking MechanismPrototype of the Inspection Robot

巡检机器人包括机器人主体，左右主驱动履带，前后摇臂履带三部分构成，中间主体箱内安装驱动电机、传动装置、控制系统及供电电源等。设计六台直流电机驱动，其中两台电机分别驱动后轮，实现机器人前进、差速转向功能，四台电机分别驱动四个摇臂，可实现摇臂单独控制。机器人采用模块化设计，便于日常维护和更换，采用前后左右对称式结构布局，使机器人的质心位于几何形心附近，有利于机器人在越障时的平稳性。

3 越障前动力学建模与分析

3.1 爬升初始时刻力学建模与分析

当障碍高度大于前摇臂长度时，在地面摩擦力较大的情况下，巡检机器人在主驱动电机驱动下，靠前摇臂与障碍垂直面的摩擦力可使机器人车体机身抬起上升，如图2所示。

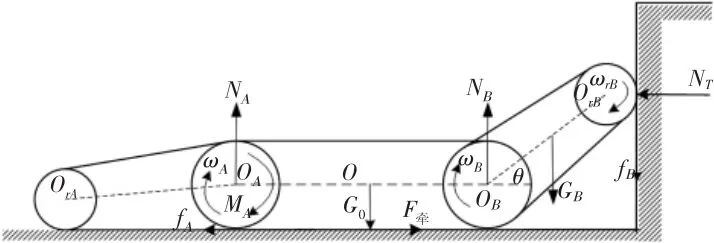
图2 爬升初始时刻受力分析图Fig.2 The Force Analysis Diagram of Climbing Initial State

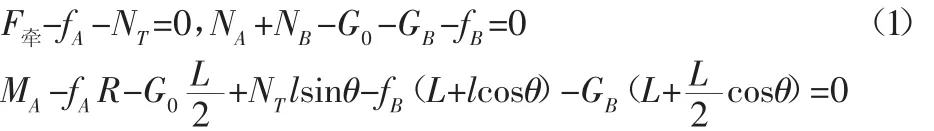
式中：fA=μAG0；fB=μBNT；μA—地面的摩擦系数；μB—台阶垂直面的摩擦系数。将机器人各几何参数带入，可求得主驱动电机驱动力矩为：

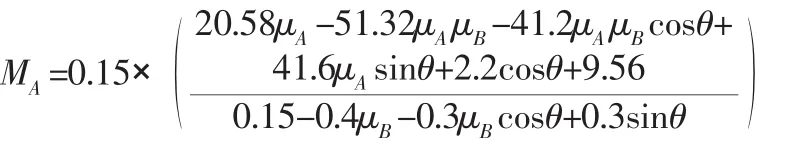
以后驱动轮中心OA为矩心，列平衡方程：

可知，主电机驱动力矩与摩擦系数μA、μB和前摇臂倾角θ有关。

经分析，当μA=μB≤0.21时，主驱动电机力矩和前摇臂倾角θ的关系，如图3所示。前摇臂倾角θ∈（0，90°），主电机驱动力矩随着前摇臂倾角增大而减小，如曲线C1所示，在摇臂角小于15°时主电机驱动力矩急剧减小，之后随着摇臂倾角增大，其变化率较平缓，驱动力矩在（15～20）Nm之间，可见当摩擦系数在该区间时，前摇臂摆角在（30～80）°之间时较合适。图中曲线C2，C3分别为μA=μB=0.10和时主电机驱动力矩和前摇臂摆角之间的关系，其变化规律是随摇臂角增大驱动力矩逐渐减小，且变化趋于平稳，同时当地面摩擦系数越小时，其主电机驱动力矩也越小。

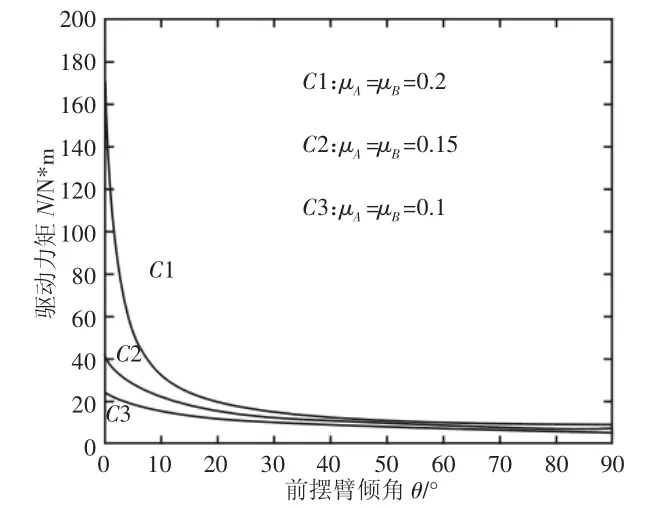
图3 μA=μB≤0.21电机驱动力矩与前摇臂倾角关系Fig.3 Relationship of the Driving Torque and Front Rockerarm Dip When μA=μB≤0.21

当 μA=μB＞0.21 时，分别绘制 μA=μB=0.4，0.6，0.8 时主电机驱动力矩与前摇臂角的关系，如图4所示。

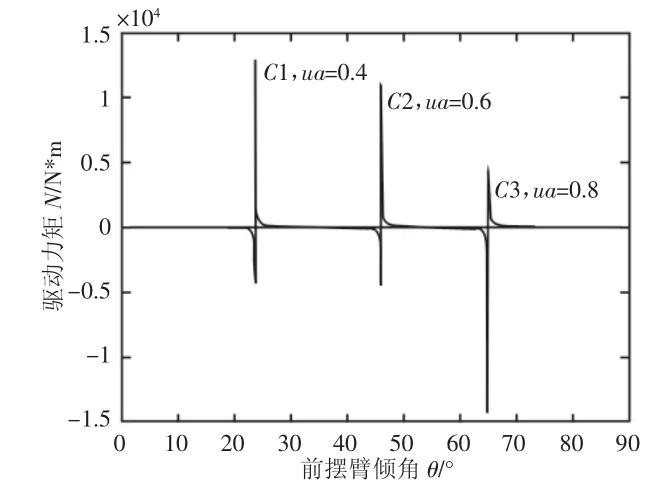
图4 μA=μB＞0.21时，电机驱动力矩与前摇臂倾角关系Fig.4 Relationship of the Driving Torque and Front Rockerarm Dip When μA=μB＞0.21

μA=μB=0.6时的主电机驱动力矩与前摆臂倾角的局部放大图，如图5所示。以下分析当μA≠μB时对主电机驱动力矩的影响。绘制μA=0.3，μA=0.5，0.7，0.9时的主电机驱动力矩图，如图6所示。可见，当地面摩擦系数μA不变时，台阶垂直面的摩擦系数μB越大，主电机驱动力矩曲线越靠右侧。绘制μB=0.3时，μA=0.5，0.7，0.9时的驱动力矩图，如图7所示。当地面摩擦系数μA不同时对电机驱动力矩基本无影响，在该越障状态下，应重点考虑台阶垂直面的摩擦系数μB对主电机驱动力矩的影响。

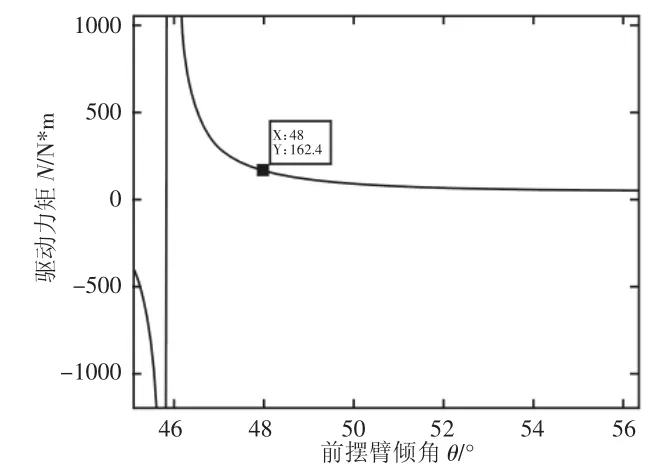
图5 μA=μB=0.6时驱动力矩和前摆臂倾角的关系局部放大图Fig.5 Relationship of the Driving Torque and Front Rockerarm Dip When μA=μB=0.6

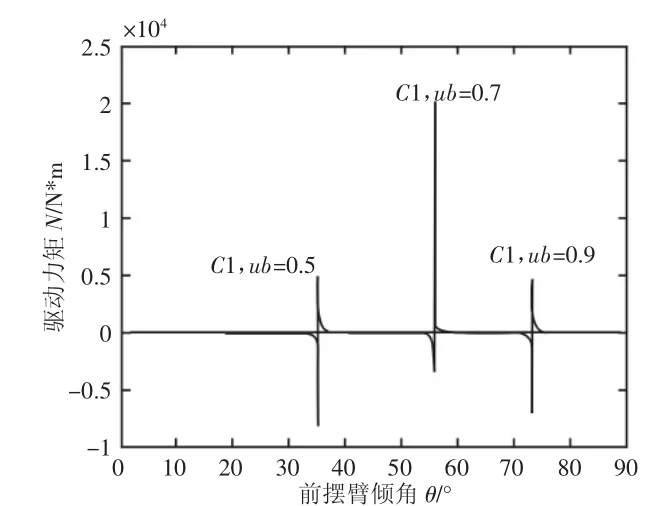
图 6 μA=0.3，μB=0.5，0.7，0.9 时驱动力矩与摇臂倾角的关系Fig.6 Relationship of the Driving Torque and Front Rockerarm Dip When μA=0.3，μB=0.5，0.7，0.9

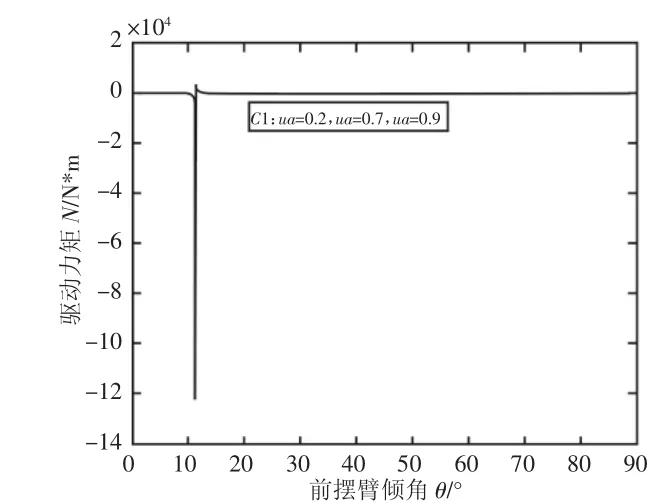
图 7 μB=0.3 时，μA=0.5，0.7，0.9 时驱动力矩与摇臂倾角的关系Fig.7 Relationship of the Driving Torque and Front Rockerarm Dip When μB=0.3，μA=0.5，0.7，0.9

3.2 爬升过程力学建模与分析

在机器人上升阶段，如图8所示。对车体进行受力分析，忽略车体旋转及履带轮转动惯量的影响，假设此时车身倾角为β，其动力学方程如式2所示。

可求得主驱动电机输出力矩：

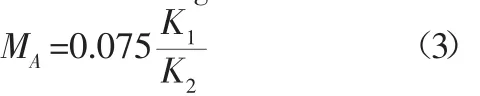
可知，该状态主电机驱动力矩与摩擦系数μA、μB、前摇臂倾角θ、车体倾斜角度β有关。首先假设μA=μB，分析前摇臂倾角θ不同时，主驱动力矩MA与车体倾斜角度β之间的关系。当μA=μB=0.5，前摇臂倾角 θ分别为 θ＝20°，40°，60°，80°时，主电机驱动力矩 MA与车体倾斜角度β之间的关系，如图9所示。可知，随着车体倾角β的增大，主驱动电机的输出力矩MA呈现单调上升趋势，而且主驱动电机输出力矩随前摇臂角θ增大而增加，C1-C4的关系，如图9所示。当前摇臂角θ=80°，且车身倾角β=80°时，主电机驱动力矩达12Nm。

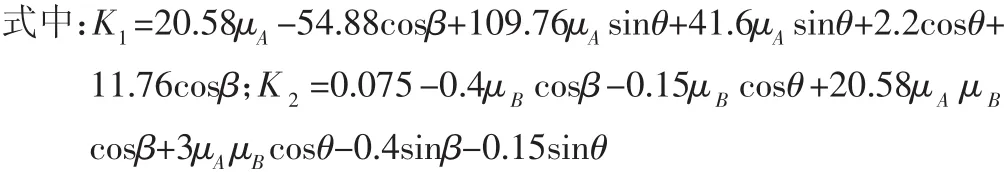
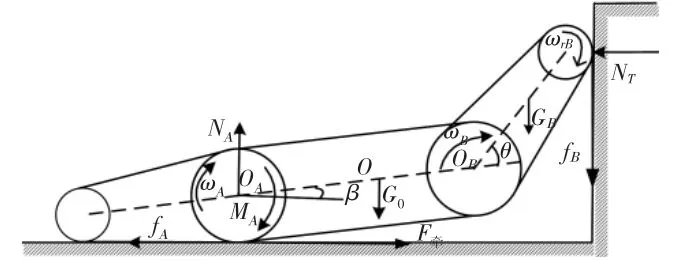
图8 上升阶段受力分析图Fig.8 The Force Analysis Diagram of Climbing Rise State

图9 前摇臂倾角不同时电机驱动力矩与车身倾角关系图Fig.9 Relationship of the Motor Driving Torque and Body Inclination with Different Front Rockerarm Dip

下面分析当前摇臂角θ不变，摩擦系数μA，μB取不同值时，主驱动力矩MA与车体倾斜角度β之间的关系。假设前摇臂角θ＝40°不变，分别绘制 μA=μB=0.3、0.5、0.7、0.9 时主电机驱动力矩 MA与车体倾斜角度β之间的关系，分别如图10的C1-C4，电机驱动力矩MA随车体倾斜角度β单调上升，且随着摩擦系数的增大驱动力矩减小，当摩擦系数μA=μB＞0.5时，变化趋势放缓。

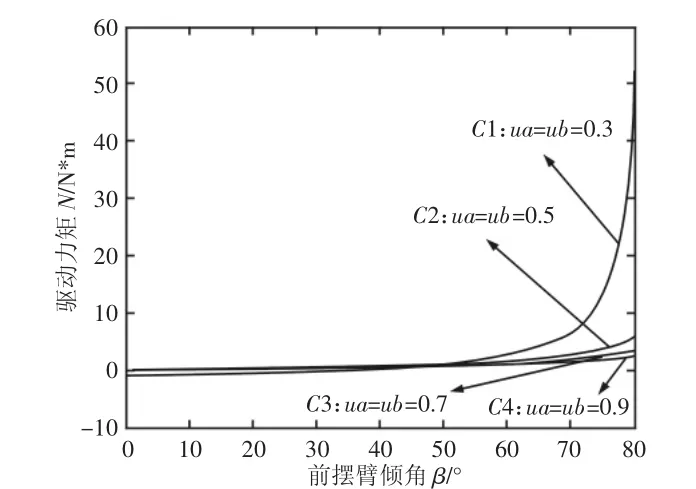
图10 摩擦系数不同时电机驱动力矩与车身倾角关系图Fig.10 Relationship of the Motor Driving Torque and Body Inclination with Different Friction Coefficient

以下分析当前摇臂角不变，摩擦系数μA，μB分别取不同值时，主驱动力矩MA与车体倾斜角度β之间的关系。假设前摇臂角θ＝40°保持不变，分别绘制当 μA=0.5，μB=0.3，0.6，0.9 时主电机驱动力矩MA与车体倾斜角度β之间的关系，C1、C2、C3，电机驱动力矩随车体倾斜角度单调上升，且随着摩擦系数μB的增大而减小。假设前摇臂角θ＝40°保持不变，当 μB=0.5，μA=0.3、0.6、0.9 时，分别绘制主电机驱动力矩与车体倾斜角度之间的关系C1、C2、C3可知台阶垂直面的摩擦系数μB对主电机驱动力矩的影响比路面摩擦系数μA敏感。

4 结论

设计了一种能适应薄煤层综采工作面地形环境的四摇臂履带式巡检机器人，介绍了该机器人的结构形式，根据达朗伯原理和牛顿—欧拉方程，分别建立了巡检机器人越障前和越障爬升过程的动力学模型，分析了不同地面摩擦系数、台阶垂直面摩擦系数、前摇臂摆角和车体倾角与主驱动电机输出力矩之间的关系，得到了一些有意义的结论，这些结论可为该结构类型的机器人的驱动电机合理选型提供理论依据，从而提高机器人的越障性能。

［1］商德勇，赵建伟，范迅.薄煤层工作面巡检机器人搭载平台应力与模态分析［J］.煤炭技术，2015，34（5）：280-283.（Shang De-yong，Zhao Jian-wei，Fan Xun.Stress and modal analysis of carrying platform for inspection robot in thin coal mining seam face［J］.Coal Technology，2015，34（5）：280-283.

［2］杨壘，商德勇，杨泽宇.薄煤层综采工作面巡检机器人摆臂动力学分析［J］.煤矿机械，2015，36（11）：120-123.（Yang Lei，Shang De-yong，Yang Ze-yu.Dynamics analysis of swinging mechanism for thin coal seam inspection robot［J］.Coal Mine Machinery，2015，36（11）：120-123.）

［3］饶伟，王建中，施家栋.关节式履带机器人越障性能分析［J］.机械设计与制造，2014（6）：39-42.（Rao Wei，Wang Jian-zhong，Shi Jia-dong.Performance analysis for obstacle negotiation of articulated-tracked robot［J］.Machinery Design ＆Manufacture，2014（6）：39-42.）

［4］段星光，黄强，李科杰.小型轮履腿复合式机器人设计及运动特性分析［J］.机械工程学报，2005，41（8）：108-114.（Duan Xing-guang，Huang Qiang，Li Ke-jie.Design and motion analysis of miniaturewheel-track-legged mobile robot［J］.Chinese Journal of Mechanical Engineering，2005，41（8）：108-114.）

［5］冯虎田，欧屹，高晓燕.小型地面移动机器人特殊运行姿态动力学建模与分析［J］.南京理工大学学报，2006，30（4）：486-490.（Feng Hu-tian，Ou Yi，GaoXiao-yan.Dynamic modeling and analysis of miniature ground-moving robot based on special moving pose［J］.Journal of NaJing University of Science and Technology，2006，30（4）：486-490.）

［6］杨林.地面移动机器人载体及搭载平台机械设计与分析［D］.南京.南京理工大学，2009.（Yang Lin.Themechanical design and analysis of the ground mobile robot carrier and the platform［D］.Nanjing，Nanjing University of Science and Technology，2009.）

［7］林小武.城市救援机器人行走系统详细设计与虚拟样机构建［D］南京：东南大学，2012.（Lin Xiao-wu.Detailed design and construction of virtual prototype for locomotion system of an urban rescue robot［D］.Nanjing：Southeast University，2012.）

［8］马金猛，李小凡，姚辰.地面移动机器人越障动力学建模与分析［J］.机器人，2008，37（3）：273-277.（Ma Jin-meng，Li Xiao-fan，Yao Chen.Dynamic modeling and analysis for obstacle negotiation of ground mobile robot［J］，ROBOT，2008，37（3）：273-277.）

［9］Kim C，YunS，Park K.Sensing system design and torque analysis of a haptic operated clinking robot［A］.Proceedings of the IEEE/IRSJ international Conference on Intelligent Robots and Systems.Piscataway N J USA：IEEE，2004：1845-1848.

［10］徐如强，韩宝玲，罗庆生.六履带机器人结构参数与越障性能的关系［J］.机械设计与制造，2012（7）：113-115.（Xu Ru-qiang，Han Bao-ling，Luo Qing-sheng.Relationship between six-track robot’s structure parameter and its performance overcoming obstacles［J］.Machinery Design ＆ Manufacture，2012（7）：113-115.）