基于PCA和LBP的考勤算法设计

王超，王洋

（长春理工大学，长春 130022）

面部识别技术是使用计算机对人的面部图像进行分析，通过图像处理显示出有效的面部特征信息，进而对人的身份进行辨认的一种技术。人的面部识别技术是近年来图像和模式识别处理领域的一个研究热点，很多研究机构及学者已经在此项技术上取得了显著的成果，并应用在许多领域［1］。由于学生管理工作是高校事务中的重中之重，由于群体特点及课堂时间的限制，采用传统的点名方式或者签到方式都会存在各种弊端，若采用面部识别技术，则可提高管理能力和效率。但由于人面部特征复杂，计算机对面部特征提取受环境影响大等因素，识别率仍有待提高［2，6］。本文设计一种结合PCA与局部二值模式的面部识别学生考勤方法，融合了主部与局部的特征，可以有效提高面部识别算法的识别率。

1 基于主成分分析的特征提取

在面部识别技术领域中，最主要的提取主部特征信息的方法就是主成分分析法（Principal Component Analysis，PCA）。其广泛应用于面部的轮廓信息提取。PCA是最早的一种多变量分析技术，起源于通信理论中的K-L变换。早在1901年，Pearson就提出了此方法，此后，Karhunan Loève等学者对该方法进行了多次修改。PCA的主要技术路线就是代表原始数据的基础上，通过线性变换将高维面部样本取样数据投影到低维数据中，使它们在低维数据中的分散程度最大化，从而更容易对面部图像进行分类显示［2］。

对于n维空间中的N个样本X1，X2，…，XN，其中Xi=(x1,x2,…,xn)可以看成N个随机变量中的第i个n维随机变量，用矩阵的形式可表示为：

对矩阵X中所有的列取平均向量，由于样本的总数为N，则可以得到所有样本的平均向量M：

进一步得出样本集X对应的总体散布矩阵，即协方差矩阵为：

根据奇异值分解定理可以求出其特征值λi及对应的特征向量由奇异值定理可知，St的正交归一化特征向量为：

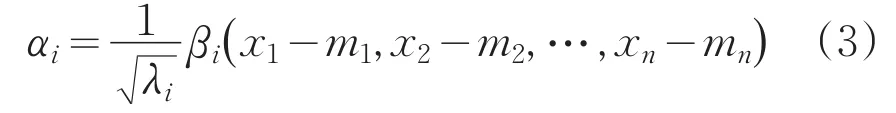
其中，i=1，2，…,n。λ1，λ2，…，λn是其特征值，且满足λ1≥λ2≥…≥λn，则其对应的特征向量为，在主成分分析中，αi可被称为这组样本的主成分，W即为这组样本的主成分矩阵。

对一个n维向量X，通过先行变换公式Y=WTX可以得到一个新的n维变量Y，即一簇投影特征向量Y1，Y2，…，Yn。这个PCA变换过程就是将变量X向W所对应的一组基进行投影，得到一组投影系数Y。在这个过程中，PCA起到了明显的降维作用。Y就称为X在这组数据下经过PCA变换后的结果［3］。

已知投影系数Y，可以通过W重构原始数据：

图1 通过PCA提取后的重构图像

图1列出了部分通过PCA提取后的重构图像，从图像分析可以看出，重构出的面部图像细节部分比较模糊，但是面部图像的全局轮廓信息非常清楚。因此PCA主要提取的是人脸的全局信息。

2 局部二值模式

局部二值模式（Local Binary Pattern，LBP）是一种具有旋转不变性和灰度不变性等优点的高效局部纹理图像描述算子［4］。在近几年的研究内，LBP算子得到不断的变化和发展，并广泛地应用于纹理图像分类、纹理处理分割、面部图像分析、目标识别等领域。

纹理分析是图像处理分析中常用的技术，它是由物体表面物理特性不同所引起的能够表示某个特定表面特征的灰度或者颜色信息。可以认为纹理图像是由很多相似的像素构成，所以直观来说纹理图像描述可提供特定图像区域的平滑、稀疏、规律性等特性。反映在图像上，纹理图像表现为颜色、亮度的周期性变化［3］。几乎所有的图像都包含了纹理信息。与其它图像特征相比，图像纹理信息反映了图像灰度模式的空间分布，也区分了图像的低频信息与高频信息，并包含了图像的表面信息及其与周围环境的联系，更好地兼顾了图像的微观结构信息与宏观信息，因此在图像分析中的纹理分析受到格外关注。

局部二值模式是一种灰度范围内的纹理描述方式［5］。通过图像点C与在其邻域内采样的n个点的差值来描述：

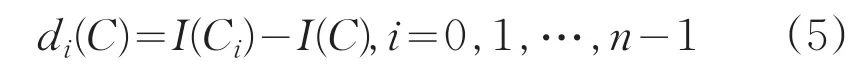
基本的LBP算子由于覆盖了一个特定半径范围内的较小区域，在应用到不同大小和频率纹理图像时受到限制，这成了LBP的最大缺点。为了适应不同大小的纹理图像特征，并保持灰度和旋转不变性的要求，Ojala［5］等对LBP算子进行了修改和改进，将最初的3×3邻域扩展到任意邻域，并用圆形邻域代替了正方形邻域，改进后的LBP算子允许在半径为R的圆形邻域内有任意多个像素点。

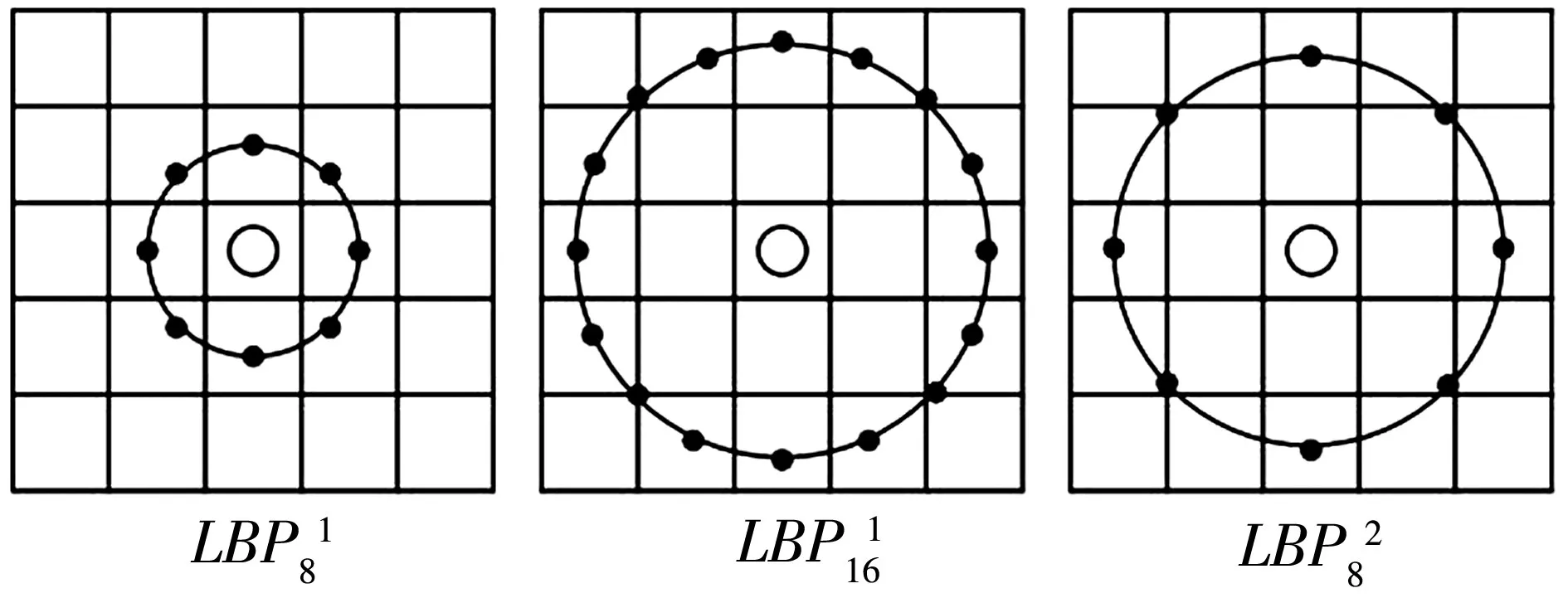
图2 Ojala提出的改进LBP算子

但是随着邻域的扩展及像素点的增加，描述子的维数也随之增加，算法的复杂度也明显加大。

3 结合PCA的局部二值模式设计

LBP的工作原理是通过将每一维以零为阈值进行二值化来实现二进制编码的。它把描述子向量空间划分为不同象限，同一象限内的描述子具有相同的编码。描述子空间的坐标可表示为：

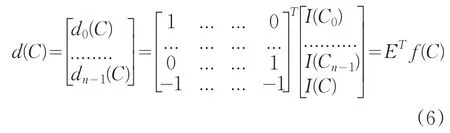
其中，C为图像块中心像素点，Ci为C的邻域像素点，是由邻域点和图像点的值组成的原始描述子向量，E是描述矩阵，是图像点的最终描述子向量。但是LBP的描述矩阵的列向量不正交，这会导致LBP的编码出现分布不均匀的情况，因此可对描述子进行变换：

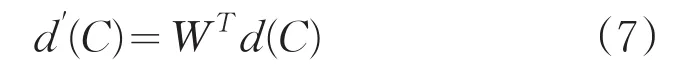
其中，W是变换矩阵。对描述子进行变换其实就是对描述矩阵进行变换：

对变换后的描述子进行阈值化得到的二进制向量为：

结合PCA变换可以保证描述子的各维间不相关，且描述子每一维的方差足够大，以确保LBP编码分布均匀。

设LBP差值描述子的协方差矩阵为：

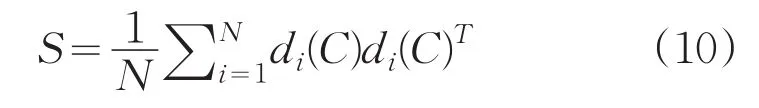
选取k个最大特征值对应的特征向量，作为变换矩阵其中k为变换后描述子所需维数。采用此变换矩阵对差值描述子进行变换，并对变换后的描述子进行LBP编码就完成了LBP的特征提取。

在LBP编码过程中增加了PCA变换，通过PCA变换，将描述子的各维间变换为不相关，也即由描述子得到的二进制码在每个比特间不相关。PCA变换在整个去相关过程中，使描述子每一维的方差最大化，即每一维在均值零附近尽量均匀分布。PCA变换能使编码值在图像总体上呈现均匀分布。另外，PCA变换还具有降维的作用。因为在LBP编码中，描述子的维数决定了编码值的数目，以及直方图特征的维数。描述子的维数越大，采样点数就越多，能利用的信息就更多，但带来的影响就是系统的复杂度也越高。PCA变换的降维作用刚好可以解决这个问题，能够简化计算，有利于更好地描述图像点。最后，PCA变换后的描述子是原差值描述子的线性组合，会大大増强编码的鲁棒性。

4 实验结果与分析

实验过程中，分别将提出的算法在ORL人脸库、YALE和FERET图像库进行验证。在ORL人脸库的训练集上随机选出250张训练图像，其中50张图像用于进行PCA变换学习，其余的200张图像分别进行常规LBP及结合PCA变换的LBP编码实验。使用400张YALE和FERET图像库的图像进行图像识别。

实验过程中，在编码的分布均匀性方面，结合PCA变换的LBP编码要明显优于常规LBP，这说明对描述子进行PCA变换具有明显效果。表1给出了对不同算法在三种权威的人脸图像库中图像识别率的统计情况，结果显示，本文提出的算法识别率均超出了PCA、LBP和CS-LBP+WPCA算法。这说明PCA变换的主部特征提取结合LBP局部二值模式起到了明显作用，主要归功于LBP和PCA的降低特征向量的维度处理，即去除了特征向量冗余部分，进而使算法的计算效率得到提高。

表1 各种算法识别率比较

5 结论

本文针对高效课堂考勤方式存在的弊端，提出了一种基于LBP与PCA变换结合的面部识别技术，在LBP二值模式提取人脸局部特征的基础上，再用PCA变换对其进行降维，通过增加LBP维数增加有效信息的获取，再通过PCA降维处理来减小算法复杂度。结合后的特征能够降低特征数据间的冗余，保证有效决策信息的保留。LBP和PCA算法的结合实现面部识别技术的有效互补。本算法在三种权威人脸图像库中进行测试，均体现了较好的识别性能，也表明本算法在面部识别上具有较好的鲁棒性。

在大数据时代的背景下，PCA与LBP的学生面部识别考勤算法体现了大数据的思维，结合智能识别技术、计算机技术和网络技术，逐渐改变传统点名方式，科学、高效的解决课堂点名的各类问题，极大的提高了课堂效率及教学质量，促进高校学生管理系统良性发展。本课题的研究可为高校管理的智能化提供一定的借鉴和参考。

［1］王竹君.基于人脸检测的移动点名系统研究与实现［D］.云南：云南大学，2014.

［2］黄金钰，张会林.LBP直方图与PCA的欧式距离的人脸识别［J］.计算机系统应用，2012，21（6）：202-204.

［3］李德福，黄新.基于二维PCA和SVM算法的人脸识别系统［J］.桂林电子科技大学学报，2017，37（5）：391-395.

［4］赵玉丹.基于LBP的图像文理特征的提取及应用［D］.西安：西安邮电大学，2015.

［5］Ojala T，Pietikäinen M，Mäenpää T.Multiresolution gray-scale and rotation invariant texture classification with local binary patterns［C］.European Conference on Computer Vision，2000，24（7）：404-420.

［6］利嘉頔，陈振学，刘成云.分块CS-LBP和加权PCA的低分辨率人脸识别［J］.光电子激光，2016，27（2）：210-216.