基于极值法和聚类分析法的测井曲线自动分层模型——以山东省胜利油井为例

初颖，吕堂红

（长春理工大学 理学院，长春 130022）

在地球物理勘探中需要利用测井资料了解地下地质情况，其中测井曲线分层是首先要完成的基础工作，通过测井分层可以实现对具有不同特点的地层进行有针对性的研究［1］。目前，分层方式主要有人工分层和自动分层两种［2］。人工分层方法是在一个区域内，测井人员依靠经验，综合各种测井数据将地层进行划分，这种方法不仅费时费力而且主观性较强，分层效果不理想；自动分层的方法则是利用已有的分层井点数据，结合丰富的测井数据实现井位分层的自动智能处理［3-4］。针对测井曲线的自动分层问题，很多学者利用不同方法进行了研究，并等到了很好的结果。彭涓［5］利用极差分析法对测井曲线自动分层问题进行了研究；覃瑞东等［6］基于Hilbert-Huang变换，给出了测井曲线自动分层的最新方法；周锦程等［7］基于高斯小波变换建立了测井曲线自动分层模型，给出了测井曲线自动分层的较好结果。

本文将利用测井数据和井位数据，根据同一层内各种测井值之间差异尽可能小，而不同层之间的同种测井值差异尽量大这一标准，在以山东省胜利某油田的1号井为标准井的前提下，采用极值聚类分析法建立自动分层模型，利用该模型进行分层，并对自动分层模型进行分析评价。以此模型来克服人工分层带来的误差。

1 模型假设

（1）在同一分层间的同种测井数据差异尽可能的小，不同层间的差异尽可能大，波动比较大；

（2）忽略因仪器或者地质引起的测井数据峰值。利用专业地质分析软件卡奔3.0导入数据后，会对各个测井数据进行分析并确定取值范围。以卡奔软件取值范围为基准，作适当调节取得合适图像时的取值范围作为该测井数据的取值范围；

（3）以胜利某油田的1号井为标准井建立数学模型，并根据此模型对2至7号井进行自动分层，将自动分层结果与人工分层结果进行比较。

2 符号说明

文中各符号所含意义如表1所示。

表1 文中各符号定义

3 模型建立和求解

首先利用极值法以垂直分辨率较高的测井曲线为主要指标来进行粗分层，大致确定层界面位置；其次利用聚类分析法，综合测井曲线中的各种指标对粗分层结果的某些邻接层进行合并，最后进行薄层合并确定最终分层。

处理的测井曲线数据中，共有66个指标，例如密度（DEN）、声波（AC）、中子（CNL）等。先利用专业地质综合分析软件卡奔3.0，确定出影响分层的主要因素，作为粗分层的分层指标。在得到对1号井的自动分层结果后，将其与人工分层的结果进行比对，结果如图1所示。经过图像分析得知，在分层点处，自然伽马曲线GR的波动比较明显并且上下频率变化较大。所以，选取GR作为对1号井分层的主要指标，进行模型中的粗分层。

图1 自动分层结果与人工分层的结果比对图

3.1 模型的数据预处理

由于测井资料数据量庞大，误差的影响因素很大，为了避免数据误差对自动分层的干扰，在对数据进行自动分层前，先对数据进行中值滤波，消除测井曲线数据中的尖峰干扰。

中值滤波法是数字信号处理中，一种常用的对信号数据进行平滑处理的方法。该算法充分地利用相邻两次中值滤波窗口内数据的相关性，在运算过程中通过对有序序列快速的对半查找和内插操作，重构有序序列并输出中值，实现中值滤波。

设测井数据序列xi(i=1,2…N)，滤波长度为2n+1，则该算法处理数据时进行以下步骤：

①以第i个测井值为中心，上下连续的n个值确定一个长为2n+1的序列，进行排序。

②取排序序列的中值，即第n+1个数据作为第i个测井值的滤波值。

③重复执行①②步骤直到曲线上的各个点计算完毕。

用Matlab软件绘出经过自动分层结果后，将其与人工分层的结果进行比对，如图2所示。

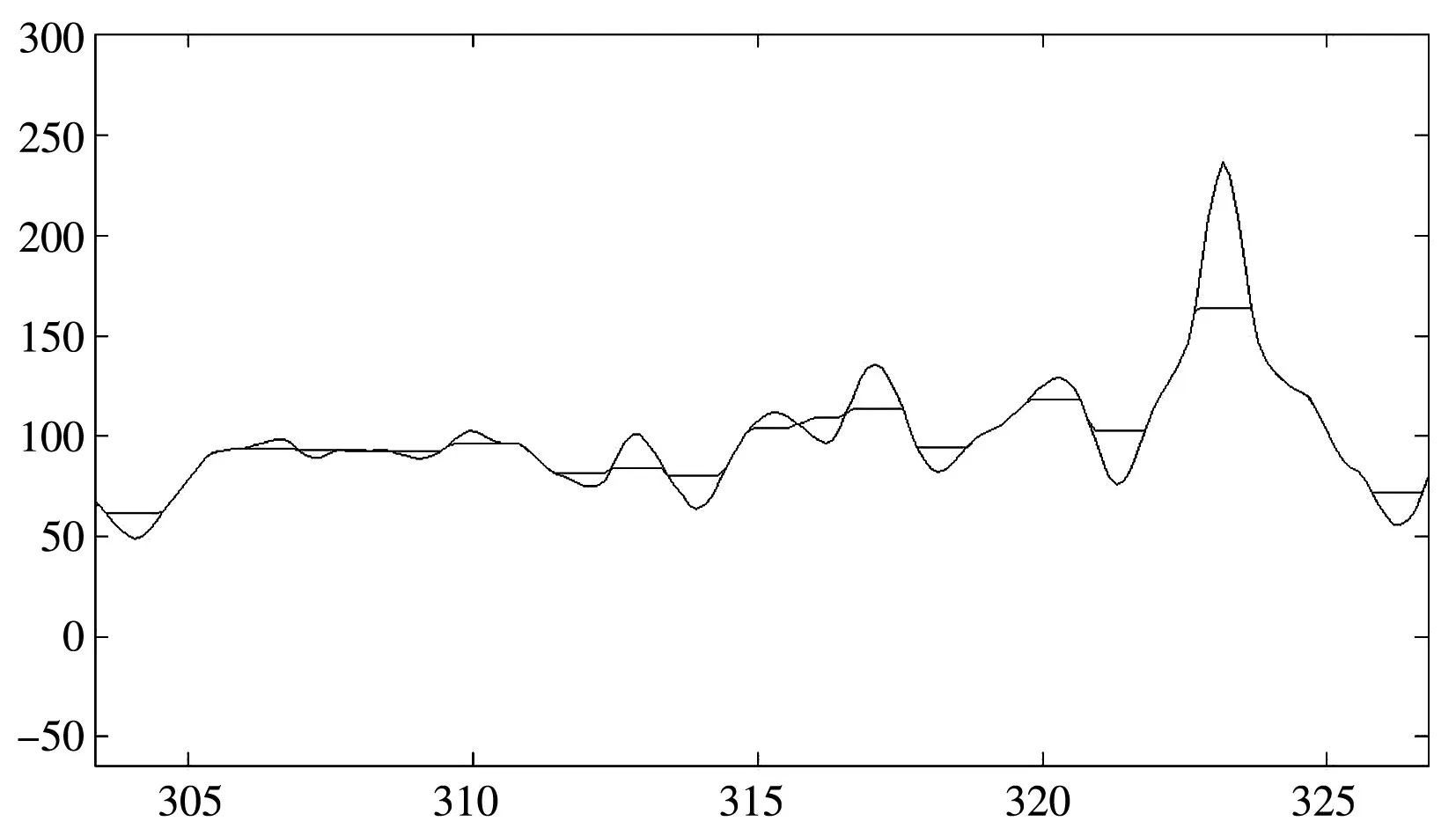
图2 自动分层结果与人工分层的结果比对图

3.2 测井曲线自动分层模型

首先采用极值法，确定分层指标函数对目标井进行粗分层，然后再综合其他指标进行聚类分析，将细层进行合并。

（1）分层指标函数Q(n)的建立

为了实现层内差异最小，层间差异最大，我们建立两层的层内差方和S：

当N值一定时，（1）式中的第一项为常数，即测井值数据的总和为常数。显然，函数Q(n)是层界面两侧两个分层数据序号n和n+1的函数。由（2）式可知，当Q(n)越大时，S越小；当Q(n)越小时，S越大。同时，当X1＜X2或者X2＜X1时，Q(n)取得极大值；当X1＜X2且Xn＞Xn+1或者X1＞X2且Xn＜Xn+1时，Q(n)取得极小值。因此选取Q(n)作为层界面函数，通过求Q(n)的极值点可以确定粗分层的层界面。

（2）处理分层指标函数Q(n)上连续相等的点

根据Q(n)上的点，利用matlab求极值后，发现许多连续的高度上对应的Q值相等，这些点都被看作为极值点，从而导致分层过密而精确性降低。如图3所示。

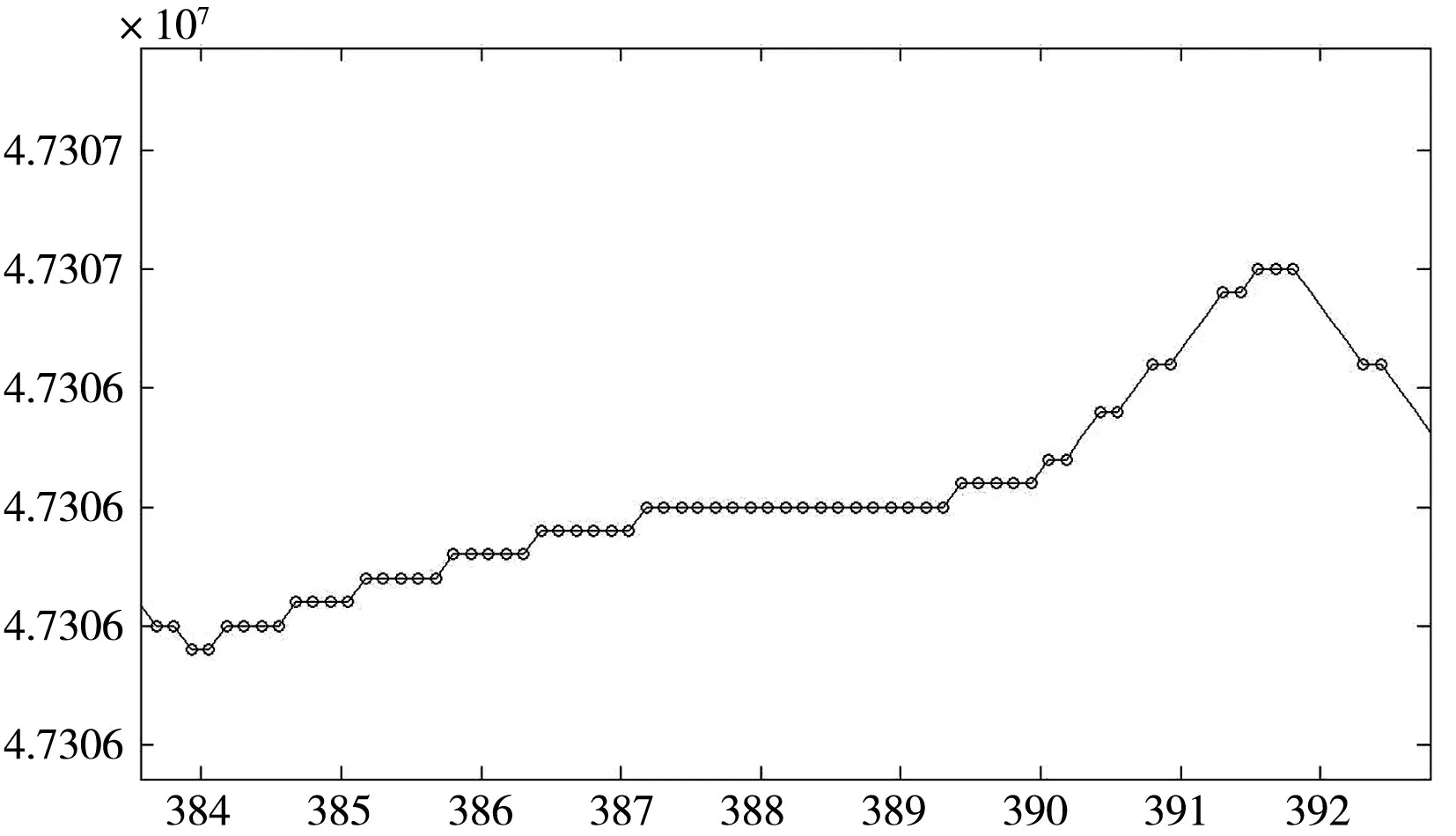
图3 Q(n)上的极值点

因此在求解指标函数Q(n)的极值之前，先对Q(n)上连续的等值点进行过滤。

设测井数据序列xi(i=1,2…N)，进行以下步骤：

①判断xi与xi+1是否相等

②如果相等继续遍历，如果不等，执行下一步

③判断是否刚经过连续相等的序列，若是则取连续序列中的中值作为xi输出，否则直接输出xi

流程图如图4所示。

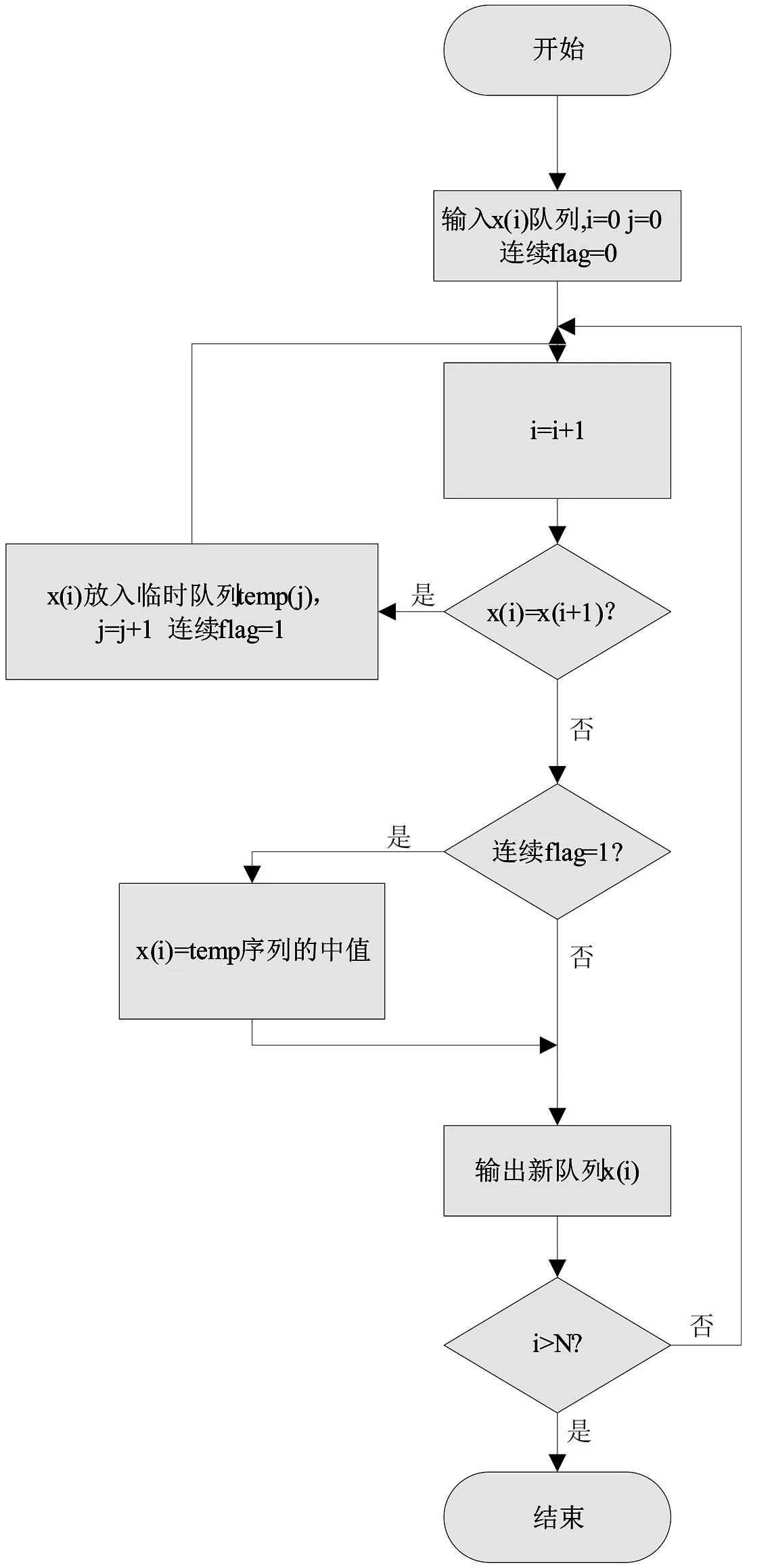
图4 算法流程图

经过处理之后的图形如图5所示。

图5 指标数据处理图

（3）聚类分析

获得GR测井曲线的极值点进行粗分层以后，考虑将其他指标一起综合考虑对现有分层进行细节调整，这里采用聚类分析法粗分层进行合并，最终通过Hmin指标对薄层进行合并，作为目标井的最终分层。按照下面步骤进行：

①归一化矩阵

由于各指标量纲不同，数值差异较大，为减小计算误差，先用以下公式对测井曲线进行归一化处理：（代码参见附录5）

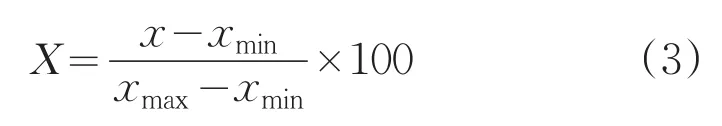
②应用马氏距离合并细层

采用马哈拉诺比斯距离（即马氏距离）作为衡量已划分出的各小层间的相似程度的分类统计量，把相似程度高且相邻的小层合并为一层。

设选取m条测井曲线进行自动分层，本文m值取为所有指标数，计算第k层与第k+1层测井值之间的马氏距离d：其中，xˉl,k为第k层上所有归一化数据的均值，为计算方便，我们先将原归一化矩阵按层均值化，作为新的矩阵X，则：

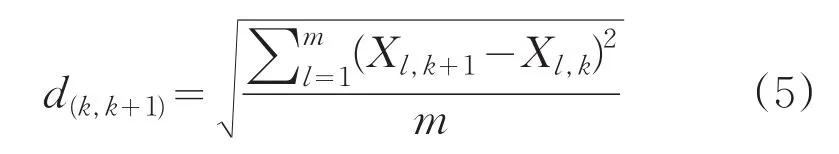
然后将d(k,k+1)与随后将讨论的最小临界距离dmin进行对比：

若d(k,k+1)≤dmin则将第k层与第k+1层合并为一个层，并重新计算该层的测井均值；

若d(k,k+1)＞dmin则认为原分层合理，不作并层处理。

接着给出最小临界距离dmin的确定方法。通常研究人员会通过经验确定dmin由于条件有限，只能通过反复分析数据寻找dmin。结合卡奔软件的绘图功能，绘出测井曲线，如图1。

选取垂直分辨率较高的的几条测井曲线分别为AC、GR、RMN、RILM、RILD，最小临界距离dmin取值为每层中这些曲线马氏距离的最小值，经过各种组合测试并反复实验，确定出最佳的dmin为AC与RMN在每层中的最小马氏距离，即：

此时绘出的图像如6所示，y轴是分层序号，横轴为井深。

③通过Hmin指标进行细层合并

由图6可见，分层点明显过多，此处我们使用自定的Hmin指标将相邻过近的层进行合并：

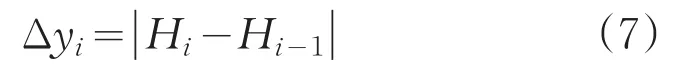
其中，H为井深度。

当Δyi≤Hmin时，将相邻两层合并；当Δyi＞Hmin时，相邻两层保持原状不变。

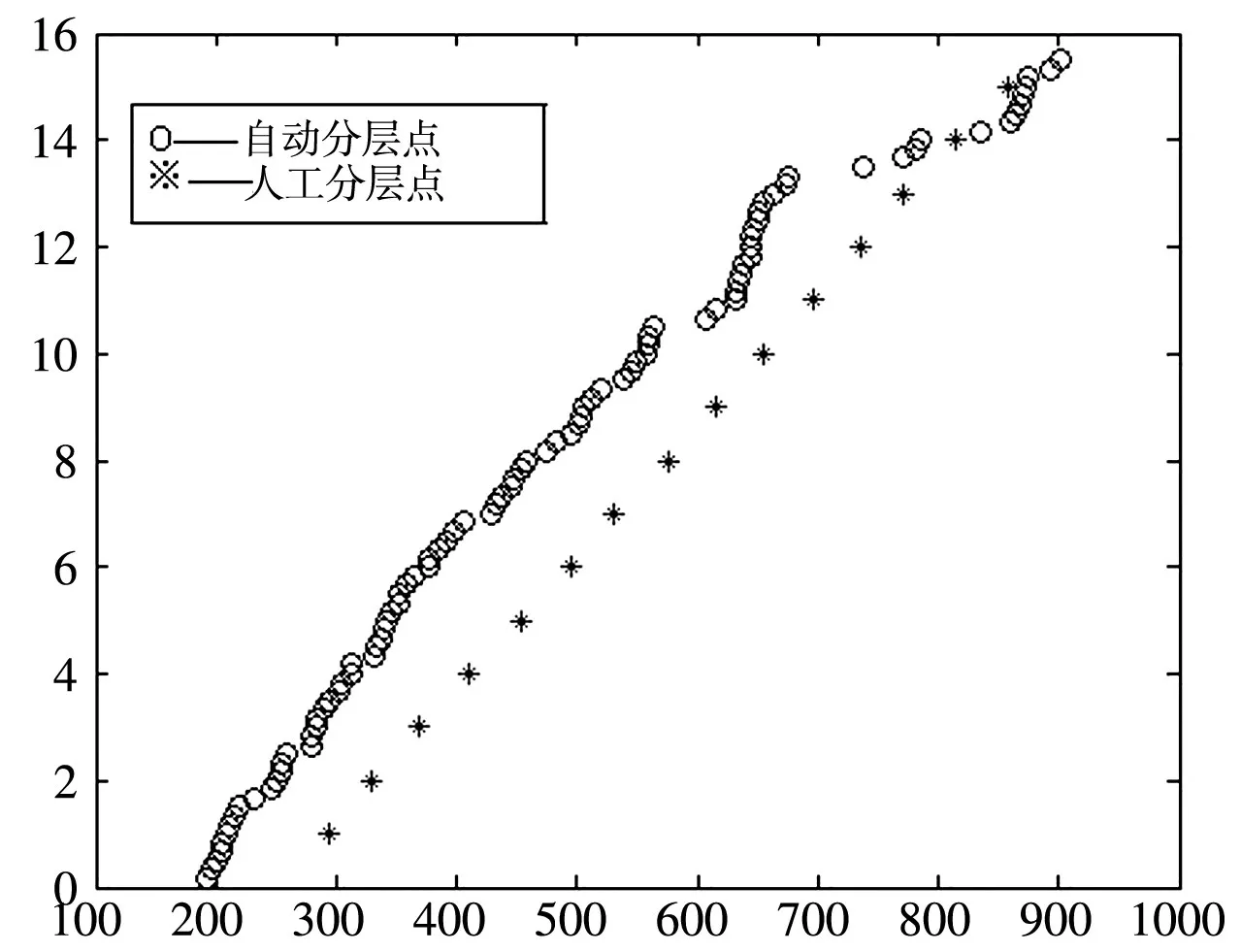
图6 各层井深数据图

因为1号井为标准井，所以为了与1号井层数相当，经过反复试验，选取Hmin=11，此时取得新的自动分层层数为17层，并与原数据做图比较，如图7所示。

图7 1号井分层点

并给出对1号井的自动分层与人工分层的井深度数据，见表2。

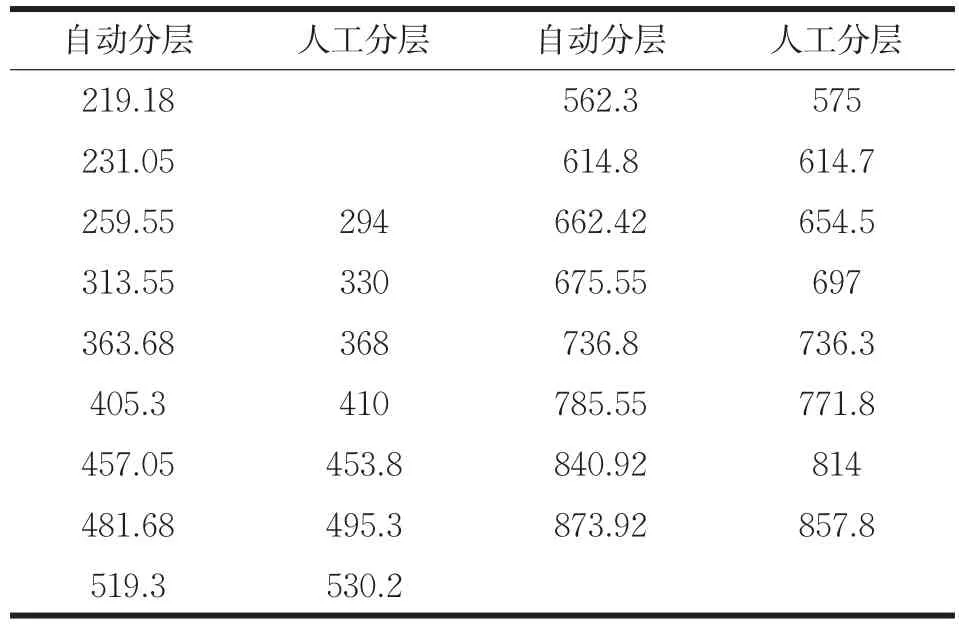
表2 1号井的自动分层与人工分层的井深度数据

4 模型检验及结果分析

4.1 对2—7号井分层

运用以上模型给出山东省胜利某油田2到7号井的分层结果。

由表1可知，以上建立的模型在1号井上的分层结果，已与标准井数据非常接近，将此模型用于2到7号井上，测出自动分层数据与人工分层数据进行对比，图像如图8-10所示。

图8 4号井分层结果对比图

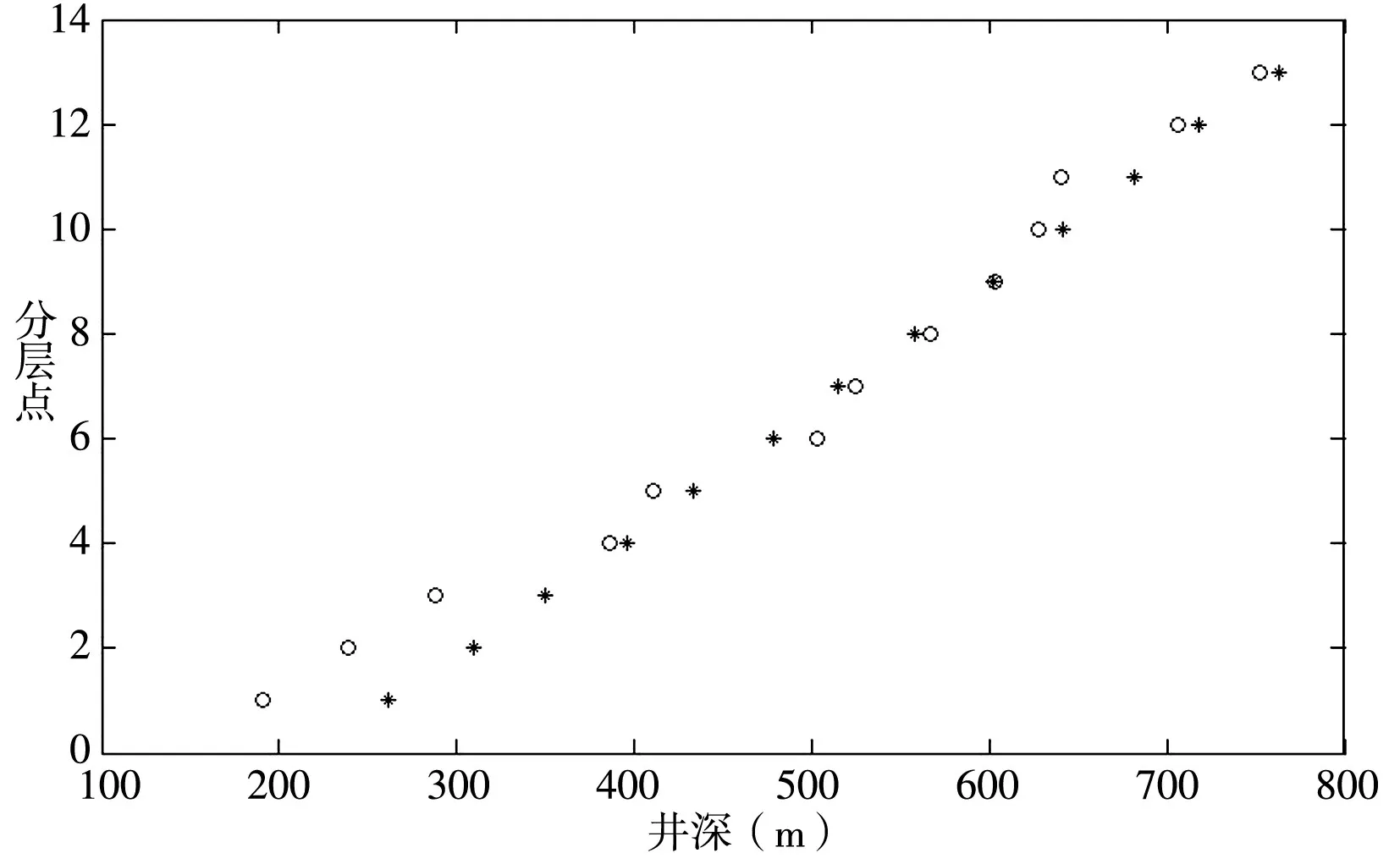
图9 6号井分层结果对比图

图10 7号井分层结果对比图

上图是4，6，7号井的自动分层结果和人工分层结果的对比。2号自动分层有五层：185.38，626，808.5，886.75（偏差较大，图片略）。3，5号自动分层都无分层。

4.2 结果分析和误差分析

（1）结果分析

由上述结果可以看出，4，6，7号井的自动分层结果贴近与人工分层结果。2，3，5号的分层结果偏差很大。所以，以1号井为标准井建立的数学模型具有一定的参考价值。但是由于1号井选取的粗分层指标为GR，选择太过于狭窄，从而引起对一些井自动分层的不适用情况。

鉴于上面的模型对于2，3，5号井的不适用情况，针对2号井进行单独选取粗分层指标，再进行自动分层。

经过对2号测井数据中的多个指标进行试验，当以RMN作为主要指标进行粗分层，取Hmin的值仍为11时候，得到2号井的自动分层结果和人工分层结果的对比图。

然而，当对3，5号经过多个指标的粗分层计算，并以Hmin=11进行计算后，得到的分层点总是很少，与人工分层差异太大。于是修改Hmin的值，再以多个指标为粗分层点进行多次分层测试，结果如下：

当Hmin=7，以RMN为主要指标时，3号井自动分层为：237.38，525.75，682.5，752.63，766.63，849

当Hmin=5，以AC为主要指标时，5号井自动分层为：237.38，525.75，682.5，742，752.63，766.63，842.88，849。

（2）误差分析

通过计算的方式确定评价函数值如表3所示。

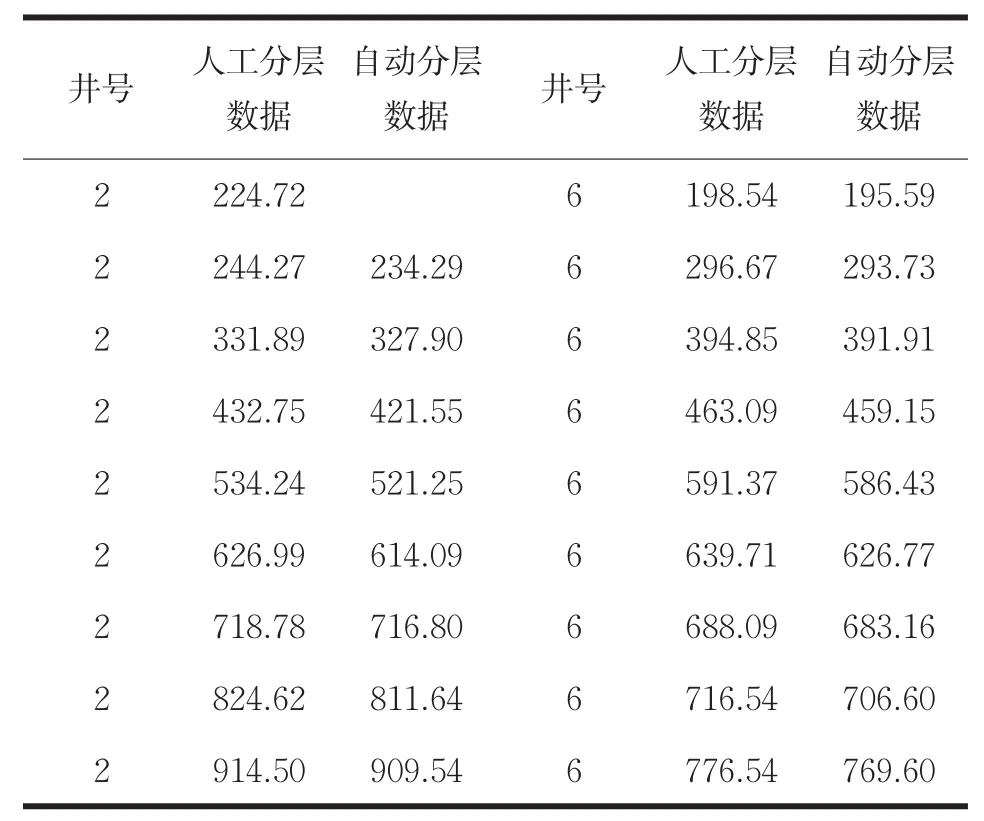
表3 自动分层和人工分层的对比结果

5 模型评价

5.1 模型优点

（1）本文建立的模型比较简单，容易求解；

（2）本文所用的知识比较初等，解决问题的方法也比较容易理解；

（3）本文在数据处理和采集方面，都是符合国家标准的，较为规范；

（4）本文在确定测井曲线的分层时，从层内差异最小和层间差异最大两方面综合考虑，比较有科学性与实用性。

5.2 模型缺点

（1）由于1号井选取的粗分层指标为GR，选择太过于狭窄，从而引起对一些井自动分层的不适用情况。

（2）由于测井曲线数据量极大，以及Hmin的不确定性，要通过很多次的测试才能得到比较合理的分层效果，模型的计算量很大。

（3）模型对于大部分目标井可以实现自动分层，而且分层结果比较均匀，但是对于特殊的目标井并不能合理分层，依旧存在不足。

（4）由于模型只是基于数据的分析，并未对目标井的地理环境以及实际情况进行考虑，所以只能作为人工分层的参考。

5.3 模型的改进

由于模型只是建立在数理分析的基础上，并没有结合地质学的相关知识，因此，在此模型的基础上，可以依据地质学专业知识，对测井曲线进行更科学的分析，并在此基础上，给予更合理的分层。

［1］肖波，韩学辉，周开金，等.测井曲线自动分层方法回顾与展望［J］.地球物理学进展，2010，25（5）：1802-1810.

［2］朱立峰.火山碎屑岩层测井曲线自动分层方法研究［D］.吉林：吉林大学，2009.

［3］纪荣艺，樊洪海，杨雄文，等.测井曲线自动分层模型设计与实现［J］.石油钻井技术，2007，35（2）：24-27.

［4］李晓飞.一种模糊篡改图像的盲鉴别算法［J］.长春理工大学学报：自然科学版，2013，36（1.2）：117-120.

［5］彭涓.基于极差分析法在测井曲线自动分层问题中的研究［J］.自动化与仪器仪表，2015，22（1）：36-38.

［6］覃瑞东，潘和平，郭博，等.基于Hilbert-Huang变换的测井曲线自动分层方法［J］.地质科技情报，2017，36（2）：258-264.

［7］周锦程，杨清亮，张伟.基于高斯小波变换的测井曲线自动分层模型［J］.自动化与仪器仪表，2017，37（4）：31-39.