改进的基于用户的协同过滤算法

张世显，李平

（长春理工大学 计算机科学与技术学院，长春 130022）

随着Internet的快速发展，网络上的信息每天都以PB级别增长。互联网虽然给我们的生活带来了方便，但是信息超载和信息迷航的问题也随之而来［1-2］。面临着如此巨大的数据，人们怎么样才能得到自己想要的信息呢？搜索引擎便应运而生，它不仅能够促进互联网的服务质量，同时还能减少用户的搜索耗时，排除掉大量干扰和无关信息［3］。但是当人们在对物品没有意愿的情况下，它并不能解决人们的需求。为了解决这一问题，个性化推荐系统应运而生，它是一种主动性的信息过滤方式［4-5］。推荐系统可以根据用户的历史信息，在用户没有需求的情况下提供精准的个性化推荐，从而引导用户获取有用的信息［6］。

协同过滤算法是目前发展比较成熟的个性化推荐算法，尤其是在电子商务中取得了非常好的效果。据悉亚马逊通过推荐算法，将其销售额提升了大约30%。但是，传统的协同过滤算法在计算相似度和预测评分时太过粗糙，没有考虑到评分对共现值的影响以及用户的兴趣迁移对评分的影响。针对这样的情况，本文主要提出两点改进：首先通过决策树模型找到评分与共现值之间的关系，实验中会通过多个模型分别测试，找出最优模型；其次引入指数时间模型来解决用户兴趣迁移问题，提高推荐的时效性。

1 相关研究

1.1 传统的协同过滤算法

协同过滤算法是推荐系统中运用最为成功的信息过滤算法［7］，主要提取用户产生的历史行为做出推荐［8］。传统的协同过滤算法主要分为基于物品的协同过滤算法（ItermCF）和基于用户的协同过滤算法（UserCF）。本论文以UserCF作为研究对象，对目标用户首先通过相似度找到K个最近邻，然后把K个最近邻产生行为而目标用户没有产生行为的物品，通过TOP-N的方式推荐给目标用户。常见的相似度计算方法有欧氏距离相似度方法（式（1））、余弦相似度方法（式（2））、皮尔逊相似度方法（式（3））、Salton相似度方法（式（4））等。通过TOP-N推荐的预测评分公式如式（5）所示。本论文中采用Salton相似度方法来计算用户的最近邻。

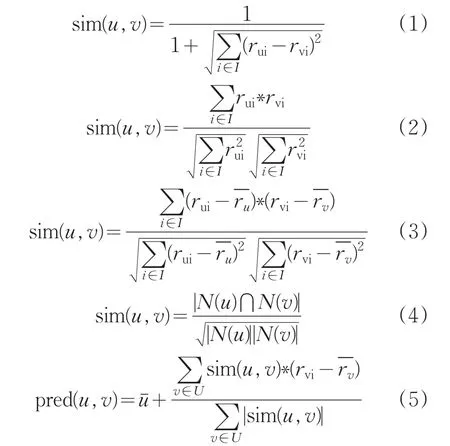
其中，U表示用户集合，I表示用户u和v共同评分过物品的集合，rui表示用户u对物品i评分，rvi表示用户u对物品i的评分表示用户u的评分均值表示用户v的评分均值。

1.2 研究现状

近几年，有很多学者对这些问题进行了研究和改进，都从不同程度上改善了这个算法的推荐准确性。文献［9］提出了一种复合指数函数作为评分权重的时间模型，在一定程度上改善了最终评分预测的结果，但是这个模型随着时间的增长下降过快不符合人类的兴趣遗忘规律。文献［10］提出了一种Logistic时间函数和用户特征相结合的方法，改善了推荐的准确度。由于这个函数值域最小在0.5，最大也不趋近于1，所以用它作为权重也不符合实际。同样文献［11］采用线性回归方式作为时间模型，分别对相似度和预测评分公式进行改进，最终也在推荐效果上有所提升，不过根据艾宾浩斯遗忘曲线，显然它也不符合。还有很多忽略用户兴趣迁移的改进［12-14］。

与上述改进方法不同，本文是根据艾宾浩斯遗忘曲线，提出一个指数时间模型，并通过权重α来控制这个模型，最后实验会分组验证这个超参数，选取一个最优的模型作为用户评分的权重。其次还会讨论选择怎么样的规则方式来映射评分和共现值之间的关系，从而改善Salton相似度，减少预测评分的平均绝对误差。

2 改进的基于用户的协同过滤算法的研究

2.1 算法的提出

2.1.1 改进Salton相似度方法

传统的协同过滤算法用式（4）所示的Salton相似度来计算目标用户的最近邻，在计算最近邻时需要构建用户u到用户v的共现矩阵。假如数据库中存有一张用户看电影的评分，如表1所示。

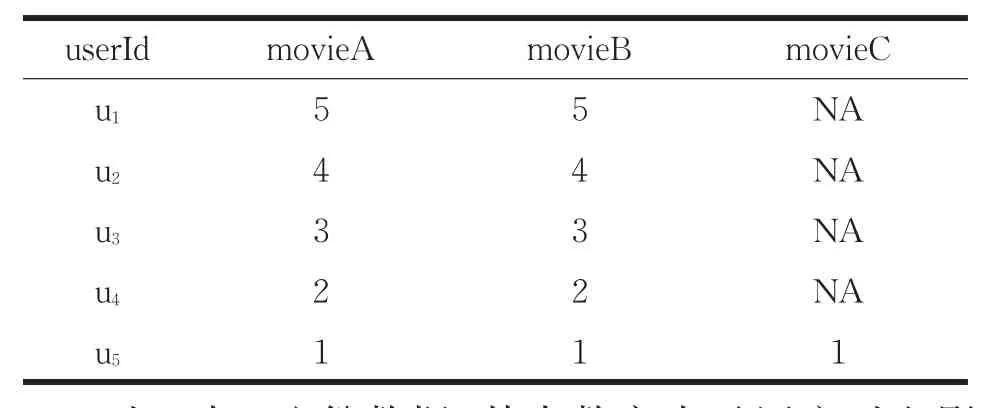
表1 不同用户对看过电影的评分（单位为分）

对于表1这份数据，其中数字表示用户对电影的评分，NA表示用户对某电影没做评分通过Salton相似度计算各个用户之间的相似度时，将会得到如表2所示的用户之间的共现矩阵。

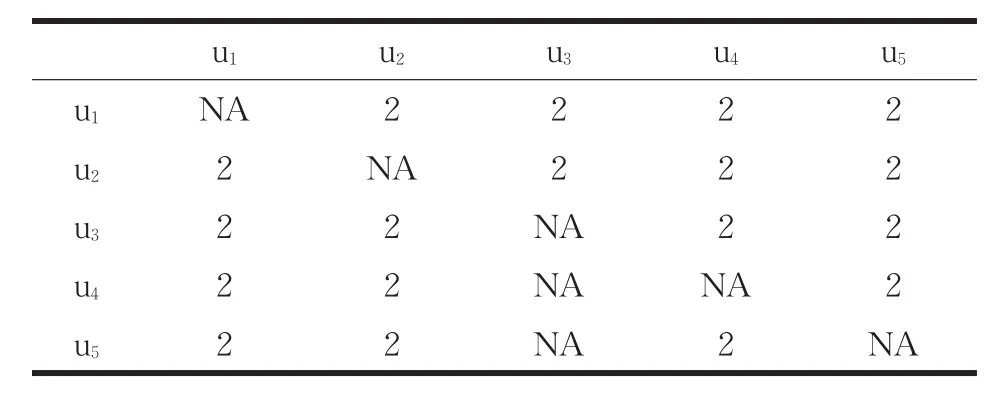
表2 不同用户之间的共现矩阵（单位为个）

表2中数字表示的是用户之间的共现值大小，NA表示相同用户不做比较即共现值为空。从表1和表2之间的映射关系就可以得出：两个用户对某个电影无论评分多少，其共现值就为1。因此，这五个用户通过Salton相似度计算得出的相似度是一样的，也就是说用户u5就可以把movieC推荐给用户u1-u4。但是根据表1可以看出u1和u5根本不存在相似性，所以用传统的Salton相似度直接计算用户之间的相似性很粗糙。为了解决这种忽略用户态度因素来计算共现值的方法，本文提出了一种决策树模型来解决上述问题。首先分析一下表1，从表1可以看出当|rui-rvi|＜=1，其共现值可以为1；当时|rui-rvi|=2，可以分三种情况：当rui=5、rvi=3时，其共现值为δ∈{0.6，0.7，0.8}；当rui=4、rvi=2时，其共现值为μ∈{0.1，0.2，0.3}，当rui=3、rvi=1时，其共现值为0；当|rui-rvi|＞2时，此时这两个用户对某个电影的态度相差太大，其共现值可以认为为0。根据上述分析，首先可以统计分析用户对电影的评分值构建简单的决策树，其次在每一条从根节点到叶节点的路径上创建一个规则。对每一条路径，从根节点到叶节点的父节点的所有条件用AND逻辑运算连接起来形成规则的条件部分（IF部分）。存放类预测的叶节点形成规则的后件（THEN部分）。本论文以用户对电影的评分为例，可以抽取IF-THEN规则如下：

Rule1：IF|u-v|＜=1 THEN C=1

Rule2：IFu=5||v=3 THEN C=δ

Rule3：IFu=4||v=2 THEN C=μ

Rule4：IF 其他THEN C=0

根据上述的IF-THEN规则，可以构造出如图1所示的决策树。

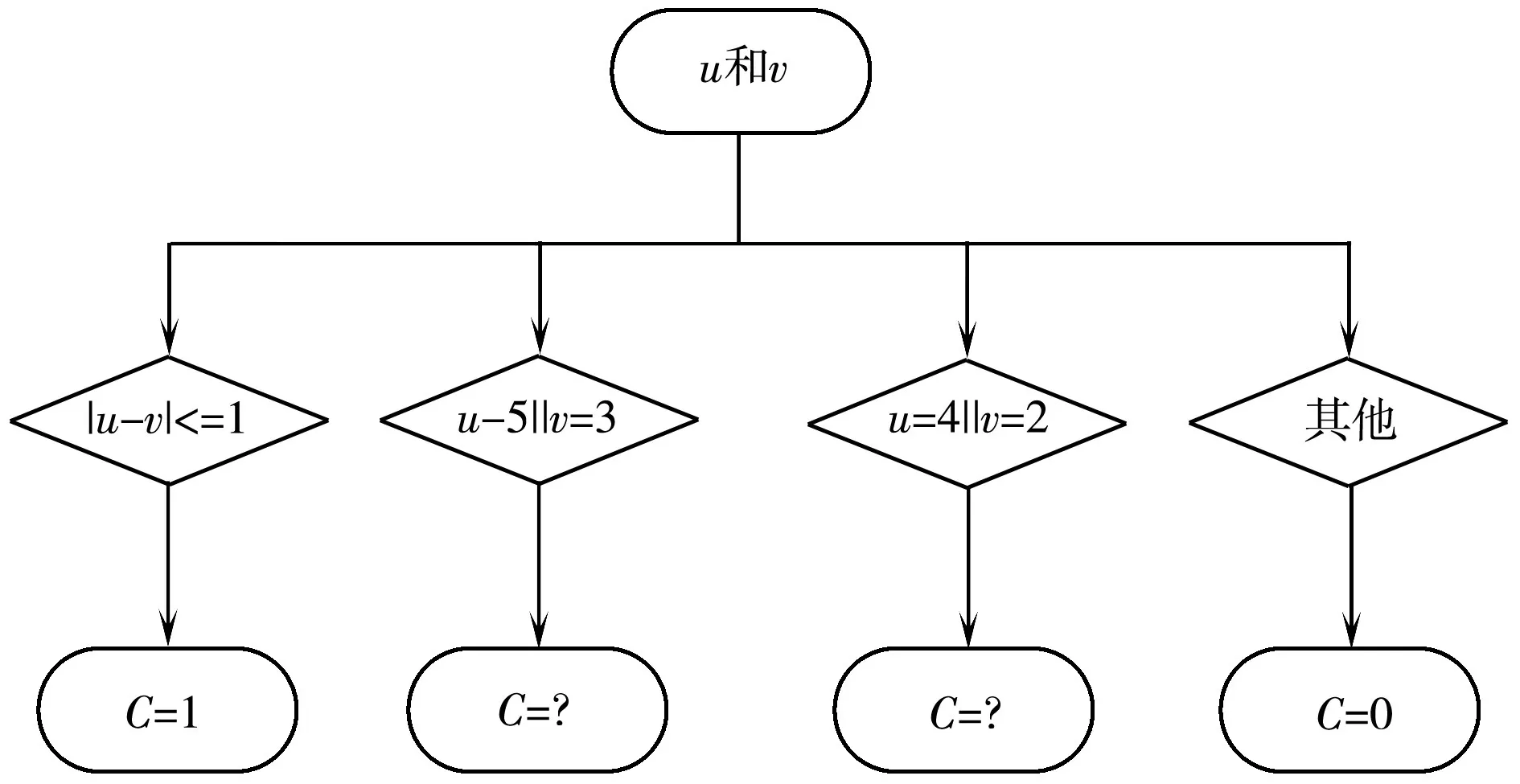
图1 用户评分和共现值关系决策树

2.1.2 改进的时间加权的预测评分模型

传统的协同过滤算法在计算用户的预测评分时并没有对已产生行为物品的历史评分做相应权重处理，也就是说没有考虑时间对用户兴趣的影响。只有当用户在同段时间或相近时间，才能有效的找邻居，进行预测评分推荐，保持推荐的时效性。举个简单的例子，假如一个人在童年时期特别喜欢看儿童类电影，在成长过程中又很少看电影，有一天他去豆瓣看电影，豆瓣会给他推荐什么电影呢？毫无疑问大部分集中在儿童类电影，显然这样是不合理的。为了解决这个问题，必须把时间较久的历史行为权重调低，通过一个动态的时间权重格式化历史行为，使推荐结果的更能反映用户的近期兴趣，达到推荐的时效性。

事实上，人类的遗忘规律和用户兴趣偏移规律是相似的［15］，因此时间模型可以参考遗忘函数给出。德国的著名心理学家艾宾浩斯对记忆的遗忘规律做了深入研究，并且绘制出了著名的“艾宾浩斯遗忘曲线”。该曲线展示了人类记忆保留的非线性递减的规律，本文受其启发提出一个指数的时间模型，来反映用户的兴趣变化，此时间模型定义如下：

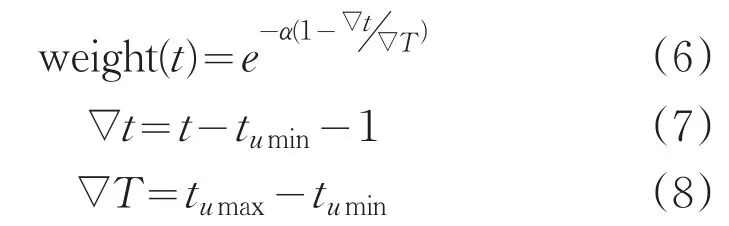
其中，t代表当前时刻，tumin表示用户u对其评价过物品的最小时间，tumax表示用户u对其评价过物品的最大时间，（7）式中减去1是为了避免评分权重为1，α∈（0，1］表示时间权重因子，α越大说明项目评分衰减速度越快，可以通过实验拟定一个合适的值。

将这个时间模型引入到式（5）中，以提高推荐的时效性，使推荐结果更倾向于当前用户的兴趣。改进后的式子如下所示：

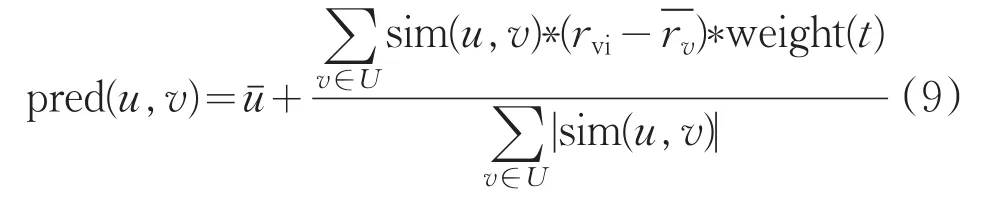
2.2 算法的过程描述

根据上述对Salton相似度的改进和利用时间加权对预测评分的改进，可以总结出改进的基于用户的协同过滤算法（R_UserCF）过程如下：

算法 R_UserCF；

输入 用户集合U，物品集合I，邻居个数K，推荐个数N，历史行为Info；

输出 预测评分矩阵M(U,I)。

Step1 根据Info信息得出用户-项目的评分矩阵R(U,I)，再根据R(U,I)通过改进的Salton相似度计算出用户u和U中其他用户的共现值，最后根据用户彼此之间的共现值就得到了用户-用户的共现矩阵Q(U,U)；

Step2 对每一个u∈U，通过Q(U,U)和改进的Salton相似度计算用户u和U中其他用户的相似度并写入用户相似度矩阵similar(u,v)；

Step3 对每一个u∈U，选取出与u相似度最高的K个用户，组成最近邻Neighbors(u,v,K)；

Step4 选出Neighbors(u,v,K)中所有产生行为的物品集合Iterms(i)，并在Iterms(i)中删除目标用户已经产生行为物品；

Step5 对每个i∈Iterms(i)，通过最近邻集合中的用户i的评分，运用公式（9）计算预测值rui，并将rui更新到M(U,I)；

Step6 返回M(U,I)，算法完成。

3 实验数据和结果分析

3.1 实验数据和评价指标

本实验使用由Grouplens提供的100K的MovieLens数据集。数据集包含了10万条记录，共943名用户对1682部电影进行5个等级的评分，评分数值为1-5。其中1代表“poor”，5表示“perfect”，其他数据则表示中间值，他们代表了用户对电影兴趣的不同程度。在试验中该数据集80%作为训练数据集20%作为测试数据集。

预测准确度是用来衡量一个推荐系统推荐能力的重要指标，本论文采用平均绝对误差（MSE）.假设原始评分集合为M={r1,r2,…,rn}，预测评分集合为N={p1,p2,…,pn}，则MAE的计算公式如下所示：

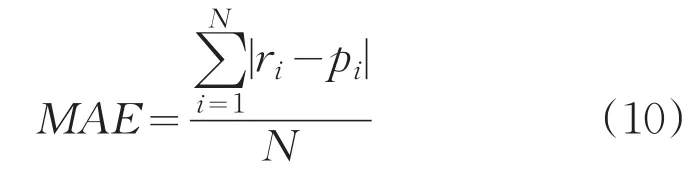
其中，N表示测试集中电影的总数。MAE的值越小，说明预测的准确率越高，产生的推荐效果越好，即推荐结果越准确。

3.2 实验参数设定

3.2.1 选取最优决策树规则

根据前面的分析，需要对三个决策树模型分别测试其平均绝对误差，来选取最优模型，此次试验选取N=20，K=10，试验结果如表3所示。

表3 不同模型及其MAE

其中A，B，C，D分别图1中的根节点值，从上述表中数据MAE值可以得出第二个模型是最优模型。

3.2.2 时间模型中的超参α

此试验主要验证时间权重因子在取何值时推荐效果达到最优，此模型选取上述模型，试验结果如图2所示。

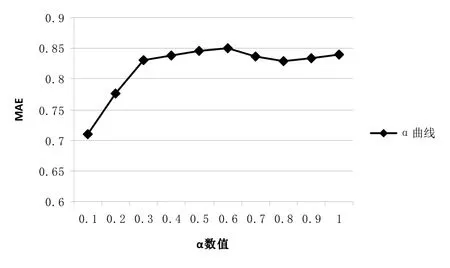
图2 不同α所对应的平均绝对误差

从上图可以明显的看出α为0.1时其平均绝对误差最小，即选取此值推荐系统得到的推荐结果达到最优。

3.3 实验对比和实验结果分析

通过上面对改进基于用户的协同过滤算法（R_UserCF）参数的优化，已经能够得出一个最优模型，下面将在不同邻居下用这个模型和传统算法（UserCF）作对比，如图3所示。

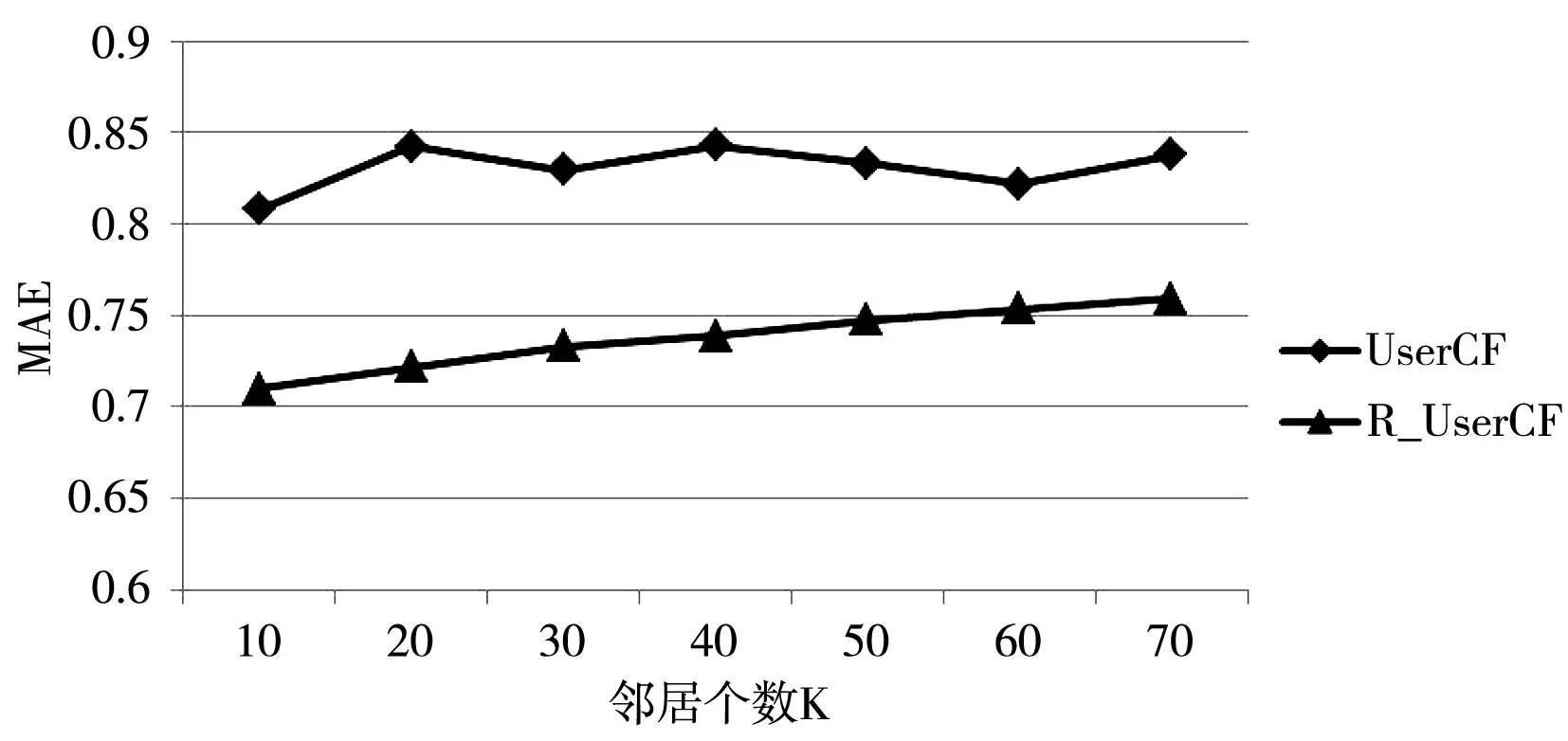
图3 UserCF和R_UserCF算法的比较

从图3可以看出改进的基于用户的协同过滤算法在同等条件下平均绝对误差都小于传统的算法，可见改进的算法在推荐中更加高效实用。

4 结论

本文在计算相似度时增加了人们的态度即通过决策树策略得出了评分和共现值的关系，并且为了应对用户的兴趣迁移问题提出了加权的时间模型，最后通过Movielens数据集验证了改进的算法在整体上都优于传统的算法。但是该算法也有两点不足之处，首先在整个算法过程中涉及到很多矩阵转换问题以及又增加了一个时间维度，因此加大了内存的开销，增加了计算的时间。其次数据集采用的是电影领域，因此该算法在应用场合上有一定的局限性。接下来主要针对这两点不足之处进行改进，尝试加入聚类模型以及选取多个领域的数据集分别进行测试实验。

［1］余力，刘鲁，罗章华.我国电子商务推荐策略的比较分析［J］.系统工程理论与实践，2004，24（8）：96-101.

［2］顾洪博，赵万平.数据挖掘算法性能优化的研究与应用［J］.长春理工大学学报：自然科学版，2010，33（1）：164-166，163.

［3］Linden G，Smith B，York J.Amazon.com Recommendations：item-to-item collaborativefiltering［J］.IEEE Internet Computing，2003（1）：76-80.

［4］邱宁佳，郭畅，杨华民，等.基于MapReduce编程模型的改进KNN分类算法研究［J］.长春理工大学学报：自然科学版，2017，40（1）：110-114.

［5］刘建国，周涛，王秉宏.个性化推荐系统的研究进展［J］.自然科学进展，2009，19（1）：1-15.

［6］Ricci F，Rokach L，Shapira B，et al.Recommender systems handbook［M］.New York：Springer，2011.

［7］黄武汉，孟祥武，王立才.移动通信网中基于用户社会化关系挖掘的协同过滤算法［J］.电子与信息学报，2011，33（12）：3002-3007.

［8］范家兵，王鹏，周渭博，等.在推荐系统中利用时间因素的方法［J］.计算机应用，2015，35（5）：1324-1327.

［9］Lai W，Deng H.An improved collaborative filtering algorithm adapting to user interest changes［C］.Information Science and Service Science and Data Mining.IEEE，2012：598-602.

［10］赵文涛，成亚飞，王春春.基于Logistic时间函数和用户特征的协同过滤算法［J］.计算机应用与软件，2017，34（2）：285-289，312.

［11］郑先荣，曹先彬.线性逐步遗忘协同过滤算法的研究［J］.计算机工程，2007，33（6）：72-73.

［12］Kharrat FB，Elkhleifi A，Faiz R.Improving collaborative filtering algorithms［C］.Proceedings of12th International Conference on Semantics，Knowledge and Grids，2016，36（5）：109-114.

［13］刘江东，梁刚，冯程，等.基于信息熵和时效性的协同过滤推荐［J］.计算机应用，2016，36（9）：2531-2534.

［14］张佳，林耀进，林梦雷等.基于信息熵的协同过滤算法［J］.山东大学学报：工学版，2016，46（2）：43-50.

［15］于洪，李转云.基于遗忘曲线的协同过滤算法［J］.南京大学学报：自然科学版，2010，46（5）：520-527.