基于存储机制的LT码编译码方法

姚渭箐, 易本顺,2

(1. 武汉大学电子信息学院, 湖北 武汉 430072; 2. 武汉大学深圳研究院, 广东 深圳 518057)

0 引 言

数字喷泉码是一种实现二进制删除信道(binary erasure channel, BEC)可靠传输的差错控制编码技术[1]。首先,将源信息均分为k个输入包,每个包长为lbit。随后,编码器源源不断产生编码包发送给接收端。接收端只需从中接收足够数量的编码包,就能实现高效译码,而无需反馈重传。Luby变换(Luby transform, LT)码[2]是数字喷泉码的第一种实现方案,具有码率不受限和编译码复杂度低等特点,现已广泛应用于广播通信、数据分发[3]、认知无线电网络、无线传感器网络[4]、云存储[5]等领域。

国内外诸多学者和科研机构在LT码的设计和优化上做了大量研究工作,并取得一定研究成果。目前的研究主要可归纳为以下几个方面。

一是设计度分布:文献[6-7]基于可译集理论来设计LT码度分布;文献[8]采用启发式算法对LT码进行度分布优化;文献[9]通过调整左度分布来设计更适用BEC的短码长LT码。

二是提出新型喷泉码:文献[10]提出一种部分恢复LT码(partial recovery Luby transform code, PR-LTC),并基于I-SDF(iterative and small degree first)分析方法进行优化；文献[11]提出SC-LT(spatially coupled LT)码,并对其置信传播(belief propagation, BP)译码的渐进性能进行研究。

三是优化编译码方法:文献[12]提出一种独立窗口LT码(independent window LT, IW-LT)不等差错保护方案,采用LT码对不同重要等级的数据分别进行独立选窗和编码;文献[13]基于算术编码理论,提出一种低冗余LT码,并对其保密机制进行优化。

综上所述,合适的度分布和编译码方法可以有效降低译码开销,提高无线通信网中的信息传输可靠性。

本文提出一种基于存储机制的(memory-based, MB)LT码的编译码方法。该方法通过改进LT码的编译码算法,来实现信息在BEC中可靠高效传输。首先,编码器采用泊松鲁棒孤子分布(Poisson-robust soliton distribution, PRSD)[14]编码并构造编码矩阵。基于输入包数量与编码矩阵行数相同这一特性,按照一定规则将源信息存储于编码矩阵中。接着,源源不断发送编码包和“存储包”。经过BEC,如果全部“存储包”都未被删除,则通过重构矩阵中的存储信息可直接得到源信息,无需进行译码过程。否则,如果部分或全部“存储包”被删除,则需结合BP算法进行译码。仿真结果表明,相比LT码的传统编译码方法,采用PRSD-MB编译码方法可以大大降低误比特率(bit error rate, BER),并加快了编译码速度。

1 LT码在BEC中传输原理

1.1 LT码编译码过程

假设k个输入包S=(s1,s2,…,sk)通过以下方法编码生成n个编码包C=(c1,c2,…,cn),n=1,2,3,…。

步骤1从度分布中随机选择一个编码包cn的度d；

步骤2随机且均匀地选取d个输入包作为该编码包的“邻接”；

步骤3将这d个“邻接”进行异或(XOR)生成一个编码包cn。

通过重复步骤1～步骤3,生成n个LT码编码包。

由于LT码是一种稀疏随机线性喷泉码,编码过程也可表示为

C=S·Gk×n

(1)

式中,S=[s1,s2,…,sk]T表示输入包矢量；C=[c1,c2,…,cn]T表示编码包矢量；Gk×n表示编码包到输入包的连接关系,通过特定方式传输给接收端[2],例如,可以将这些连接关系放到编码包的头部位置,或者将产生度和“邻接”的伪随机数发生器的种子事先告知接收端,收发双方可以通过同步来实现成功译码。

当在BEC中传输,一些编码包可能不能被接收到,图1中灰色部分表示删除的编码包以及相应的编码矩阵列。

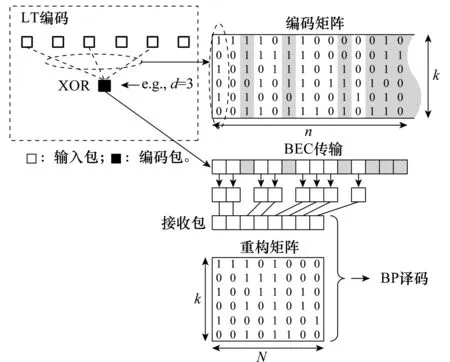
图1 LT码编译码过程Fig.1 LT encoding and decoding process

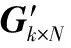
步骤1度数为1(d=1)的编码包直接译码。

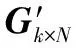
步骤3重复步骤1和步骤2,直至译码完成。

1.2 度分布

根据LT码编译码过程可知,度分布对LT码的性能影响至关重要。文献[2]指出,一个好的度分布需满足两个设计目标:①译码成功所需的平均编码包数量尽可能少,确保LT译码成功的编码包数量对应于确保输入包全部译出的编码包数量；②编码包的平均度数尽可能小,平均度数是生成一个编码包所需的平均XOR运算次数,因此平均度数决定了编码复杂度,而译码复杂度则是平均度数乘以译码成功所需编码包数量。常见的LT码度分布有理想孤子分布(ideal soliton distribution, ISD)和鲁棒孤子分布(robust soliton distribution, RSD)[2]。

(1) ISD

ISD表示的是一种理想情况,即在每次译码迭代中,只有一个度为1的编码包,并且在每次迭代译码之后,只出现一个新的度为1的编码包。其度分布函数为

(2)

式中,d为每个编码包的度；k为输入包数量。

然而,这种度分布的实际性能很差,一个很小的偏差就会导致度为1的编码包消失从而造成译码终止。

(2) RSD

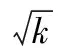
首先,定义一个函数

(3)

然后,将ρ(d)和τ(d)相加,并做归一化处理得到RSD为

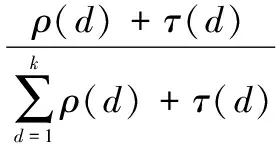
(4)

式中,d为每个编码包的度。

尽管RSD优于ISD,但采用RSD进行LT编码所产生的编码包多为度数较大的编码包,在译码过程中可能会由于缺少足够的度数较小的编码包而导致译码中断。

2 MB机制的LT码编译码方法

2.1 MB编码方法

根据式(1)可知,编码矩阵Gk×n的列数对应产生的编码包的数量n,每一列中的元素“1”可以看作该列对应的编码包与输入包之间存在连接关系;编码矩阵的行数对应输入包的数量k,每一行中的元素“1”可以看作该行对应的输入包与编码包之间存在连接关系。也就是说,编码矩阵中每个为“1”的元素Gi,j表示第i个输入包与第j个编码包之间的连接关系。可以看出,输入包的数量与编码矩阵行数相同。基于这一特性,按照一定规则将源信息存储于编码矩阵中来改进编码算法。

首先,将输入包组成一个k×l的矩阵Sk×l,将其每一列依次作为编码矩阵Gk×n的附加列,生成新的编码矩阵Gk×(n+l)。此时,新编码矩阵的行数仍为k,而列数增加了l列。

随后,为了区分附加列和原编码矩阵列,考虑在编码矩阵Gk×(n+l)的第k行后增加几行作为“标志行”。经过BEC以后,编码包在传输过程中的顺序被打乱,为了能够将输入包的每bit信息正确恢复到各自原始的位置,采用十进制数字对矩阵Sk×l的列顺序进行从低到高标注,然后将十进制转换为二进制。“标志行”的行数由二进制标志的位数确定,将这些二进制标志分别存储于各个“存储列”对应的“标志行”中,而其他列对应的“标志行”的每个元素设置为0。

最后,通过上述存储机制,产生新的编码矩阵G(k+num)×(n+l),其中,num为二进制标志的位数。“标志行”只起到标注作用,而不参与实际编码,也就是说,原来基于Gk×n产生的编码序列保持不变。为了在编码序列中增加“存储列”对应的编码包,直接假设“存储列”对应的编码包中每bit都为1。

为更清楚说明,如图2所示,以输入包长度l=3 bit为例,改进的编码算法如下:

步骤1从度分布中随机选择一个编码包的度d。随机且均匀地选取d个输入包作为该编码包的“邻接”。将这d个“邻接”进行XOR生成一个编码包。同时,这个编码包到输入包的连接关系表示为编码矩阵的对应列。

步骤2重复步骤1产生n个编码包和编码矩阵Gk×n。

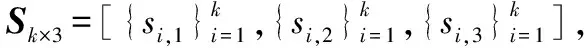
(5)

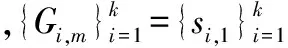
步骤4将“1”“2”“3”作为标志对“存储列”进行排序,其他列标志为“0”。首先,将十进制“0”“1”“2”“3”转换为二进制“00”“01”“10”“11”。然后,将这些二进制标志存储于编码矩阵的附加行,生成新的编码矩阵为

(6)

式中,第k+1行和第k+2行为“标志行”。[G(k+1),m,G(k+2),m]=[0,1]；[G(k+1),(m+1),G(k+2),(m+1)]=[1, 0]；[G(k+1),(m+2),G(k+2),(m+2)]=[1,1],而“标志行”的其他元素设置为0。

步骤5对应于“存储列”的每个编码包中的3 bit都设置为1,称为“存储包”。

2.2 MB译码方法

经过BEC传输,编码数据包的顺序被打乱,一些编码包可能不能被接收到。“存储包”必然也要面临被删除的可能性,尽管“存储包”不用参与译码,但是“存储包”中的存储信息可以恢复输入包中某些bit。

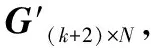
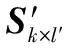
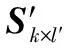
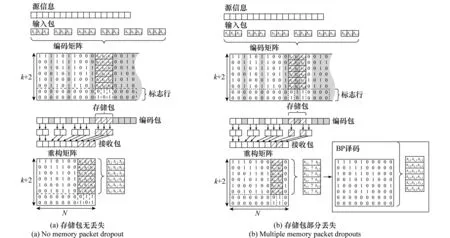
图2 MB编译码方法Fig.2 MB encoding and decoding method

改进的译码算法如下:

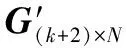
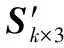
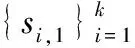
步骤4如果所有标志未被检测出,则表示所有“存储包”丢失,采用BP算法进行译码。

2.3 系统开销分析

接收端的译码器根据“存储包”全部接收、部分接收以及全部丢失的不同情况,分别采取3种不同的方式对输入包进行译码恢复。因此,MB译码复杂度也是随实际情况发生变化。然而,MB编码过程中增加“存储列”和“标志行”的操作增加了稍微的编码复杂度,必会产生一定的耗时。输入包采用RSD-MB方法(参数:k=100,c=0.1,δ=0.5)进行编码,平均一次编码耗时随附加列数增加的变化情况如图3所示。可以明显看出,随着附加列数的增加,平均一次编码耗时也随之略微增大。

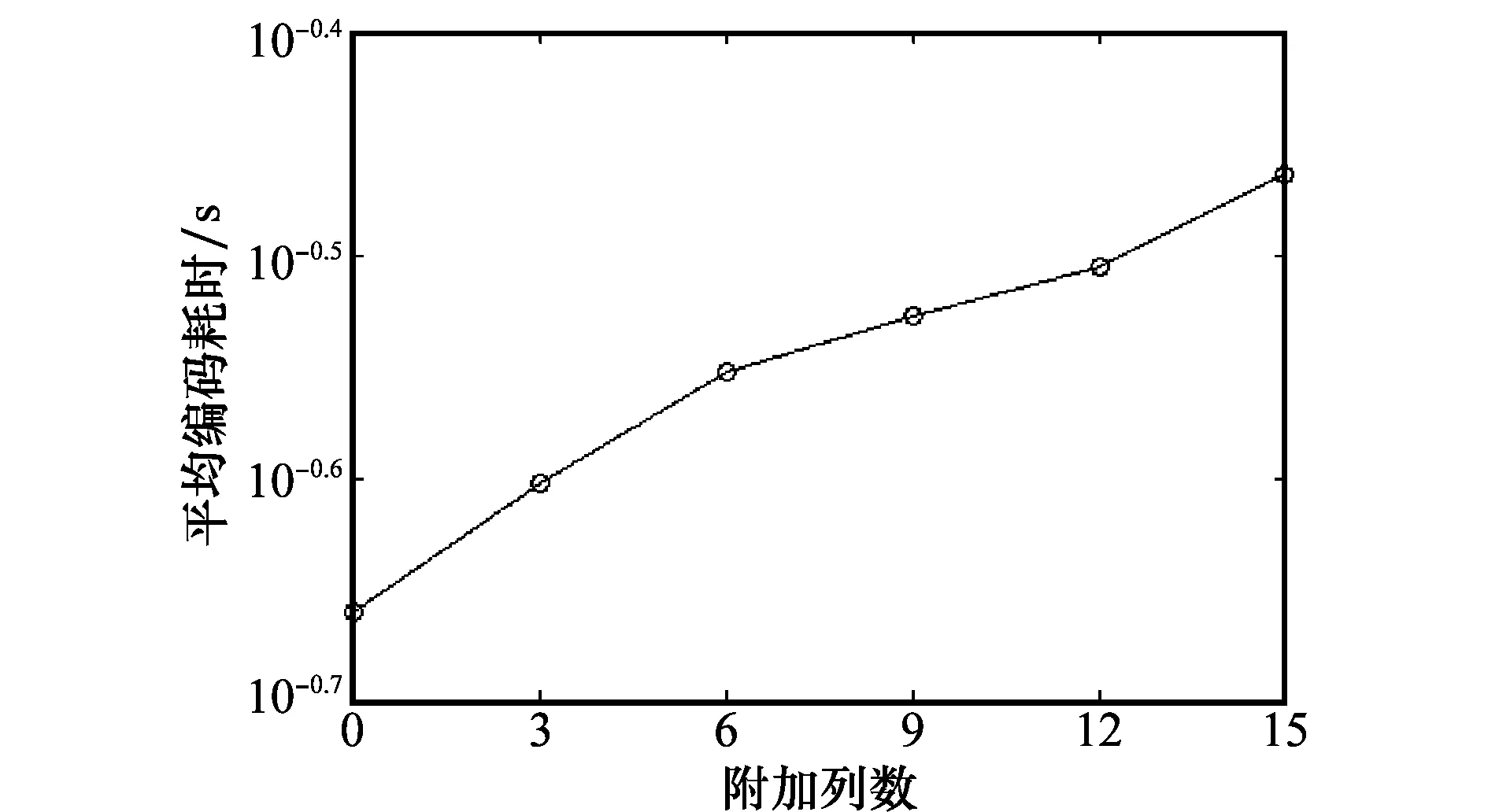
图3 RSD-MB算法平均编码耗时Fig.3 Average consuming time per encoding process ofRSD-MB algorithm

另一方面,当k与l的比例较大时,仅需少量“存储包”就能存储大量甚至全部源信息,MB编译码方法的差错控制性能更强。因此,为获得较高的译码成功率,发送端的编码器需要将源信息均分为尽可能多的输入包。但过多的输入包数量会导致编译码XOR运算次数增多,即编译码复杂度升高,从而牺牲了译码效率,降低编译码速度。

综上所述,为了在保证高译码成功率的同时,又能提高编译码效率,考虑采用文献[14]中提出的PRSD作为编码器的度分布。采用PRSD进行编码能产生大量度数为1的编码包。在译码过程中,度数为1的编码包直接译码,而无需进行任何XOR操作,从而降低了译码复杂度,降低译码耗时。因此,基于存储机制的编译码方法与PRSD相结合,能在译码成功率和编译码效率之间建立一个好的性能平衡。

2.4 PRSD

为进一步提高译码成功率和编译码效率,本文采用性能更优的PRSD[14]。大量的研究工作证实,度分布中某些度数的比例对LT码的可译码性起主导作用。LT码可通过调整这些度数的比例获得良好的性能。度2(d=2)在度分布中所占比例最高。文献[15]研究了LT码在BEC中的性能,并且推导出当BP译码器的误码率趋近于0时度2比例等于1/2。

因此,考虑通过合理地调整泊松分布(Poisson distribution, PD)中度2的比例来改进LT码性能。改进的泊松分布(improved Poisson distribution, IPD)由θ(d)表示为

(7)

θ(d)与RSD中的函数τ(d)进行归一化,得到PRSD函数表达式为

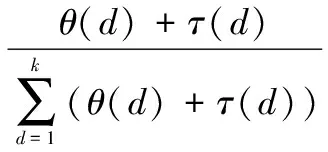
(8)

参数λ是θ(d)函数中的一个正常数。为了满足一个好的度分布的设计需要[2],编码包的平均度数越小越好。因为RSD由ρ(d)和τ(d)构成,PRSD由θ(d)和τ(d)构成,所以平均度数的问题可转换为θ(d)和ρ(d)均值的问题。θ(d)和ρ(d)均值的表达式为

(9)

(10)

ISD表示的是一种理想情况,即在每次译码迭代中,只有一个度为1的编码包,并且在每次迭代译码之后,只出现一个新的度为1的编码包[2]。理想情况下,λ的参数值可通过θ(d)和ρ(d)均值相等来推出。ρ(d)均值将会随k增加而增大。基于PD的数学特性,当k<20时，PD近似于二项分布。因此,从k=20点推导出λ的参数值。根据当k=20时E[θ(k=20)]=E[ρ(k=20)] =3.577,得到λ≈3.04。

RSD产生大量度较高的编码包,能保证所有输入包参与编码,但可能由于度1的编码包消失而导致译码过程某步中断;IPD能够产生足够多的度1的编码包来保证译码持续进行,但可能因为度较高的编码包数量较少而致使输入包不能全部被译出。因此,基于结合RSD和IPD两种度分布的特点,采用PRSD进行LT编码,能同时提高LT码编译码效率和译码成功率。

3 性能仿真及分析

本节对PRSD-MB的性能进行评估。根据表1选择参数,输入包分别采用RSD-BP、PRSD-BP、RSD-MB和PRSD-MB进行编码,然后基于10 000次迭代结果对这4种方法的性能进行分析和比较。

表1 源信息的参数选择

当α=0.2(α为删除概率)时,BER对应译码开销(ε=(N-k)/k)的变化情况如图4所示。

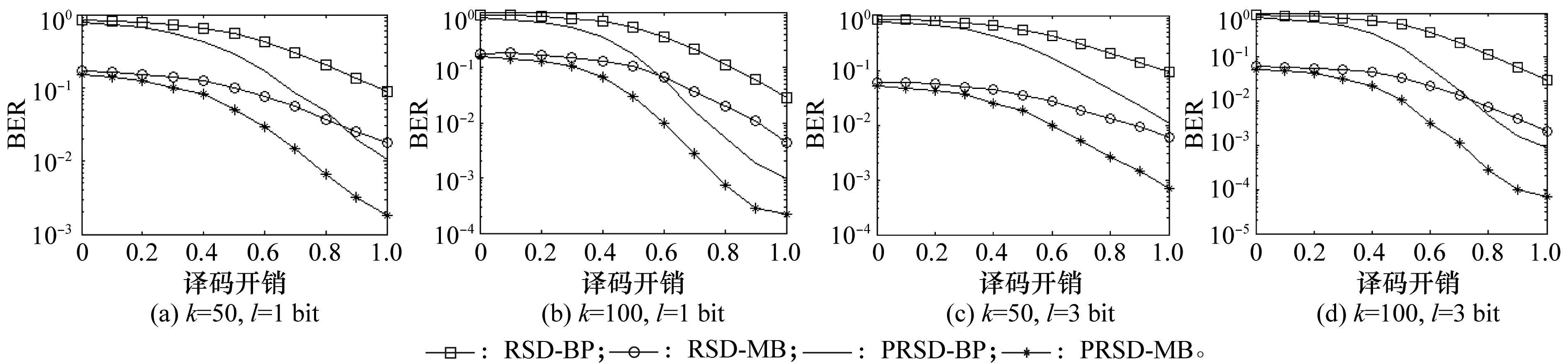
图4 不同译码开销下RSD-BP、PRSD-BP、RSD-MB和PRSD-MB的BER对比(α=0.2)Fig.4 BER versus overhead for RSD-BP, PRSD-BP, RSD-MB and PRSD-MB (α=0.2)

可以看出,相比RSD-BP、PRSD-BP和RSD-MB,PRSD-MB具有更好的差错控制性能。不同k和l下,这4种方法的BER随着ε增加而逐渐降低。当ε相同时,PRSD-MB的BER最低,其次是PRSD-BP和RSD-MB。而删除概率对传统RSD-BP的影响最大。例如,图4(d)中,当ε=0.5时,参数为k=100和l=3 bit的PRSD-MB的BER仅为10-3,比其他3种方法低很多。尤其相比于RSD-BP,PRSD-MB的BER降低了53.5%。

当ε=0.5时,BER对应α的变化情况如图5所示。很明显,随着α增加,BER逐渐升高。相比其他3种方法,PRSD-MB在不同α时,都能获得更好的差错控制性能。当α=0.2,ε=0.5时,编译码平均耗时对应k的变化情况如图6所示。尽管PRSD-BP和PRSD-MB的性能表现很相似,但是他们都优于RSD-BP 和RSD-MB。例如,参数为k=100和l=3 bit时,相比RSD-BP和RSD-MB,PRSD-MB编译码速度分别加快了44.0%和42.5%。

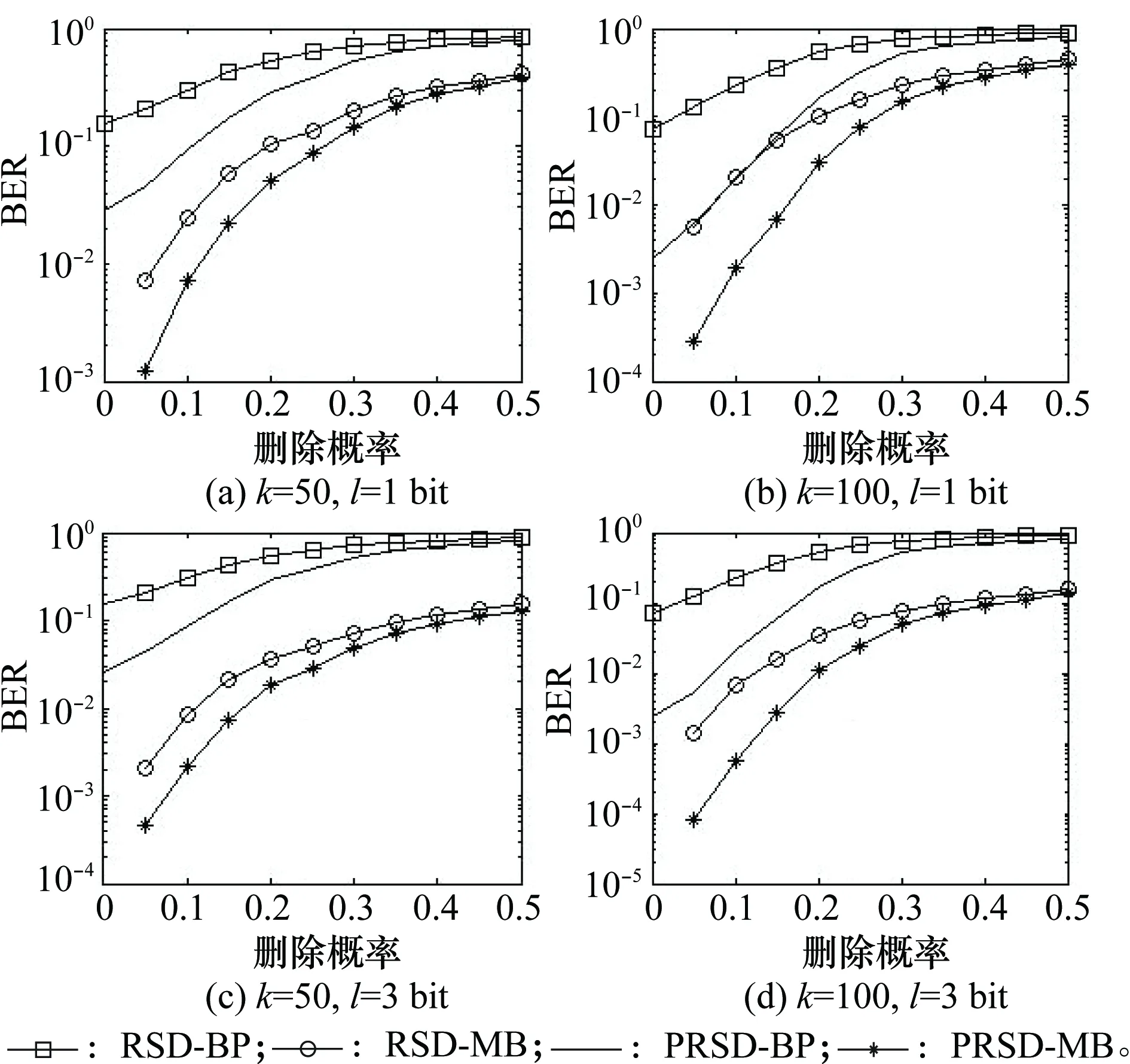
图5 不同删除概率下RSD-BP、PRSD-BP、RSD-MB和PRSD-MB的BER对比(ε=0.5) Fig.5 BER versus erasure probability for RSD-BP, PRSD-BP,RSD-MB and PRSD-MB (ε=0.5)

4 结 论

本文提出一种适用于BEC的基于存储机制的LT码的编译码方法。发送端的编码器采用PRSD产生普通编码包,同时通过将源信息存储于编码矩阵产生一些“存储包”。经过BEC后,接收端的译码器根据“存储包”全部接收、部分丢失以及完全丢失的不同情况,分别采取不同方式进行译码。尽管添加和检测存储信息的操作会轻微增加运算量,但总体上对编译码复杂度的影响很小,提高了译码成功率和编译码效率。仿真结果表明,相比传统方法,PRSD-MB能够提高信息在BEC中传输的可靠性和效率。

[1] MACKAY D J C. Fountain codes[J]. IEEE Proceedings-Communications, 2005, 152(6): 1062-1068.

[2] LUBY M. LT codes[C]∥Proc.of the 43rd Annual IEEE Symposium on Foundations of Computer Science, 2002: 271-280.

[3] LEE K, KIM C, LEE S H, et al. Rateless code based reliable multicast for data distribution service[C]∥Proc.of the IEEE International Conference on Big Data and Smart Computing, 2015: 150-156.

[4] DU W, LI Z, LIANDO J C, et al. From rateless to distanceless: enabling sparse sensor network deployment in large areas[C]∥Proc.of the 12th ACM Conference on Embedded Network Sensor Systems, 2014: 134-147.

[5] ANGLANO C, GAETA R, GRANGETTO M. Exploiting rateless codes in cloud storage systems[J]. IEEE Trans.on Parallel and Distributed Systems, 2015, 26(5): 1313-1322.

[6] YEN K K, LIAO Y C, CHANG H C. Design of LT code degree distribution with profiled output ripple size[C]∥Proc.of the IEEE Workshop on Signal Processing Systems, 2015: 1-6.

[7] YEN K K, LIAO Y C, CHEN C L, et al. Modified robust soliton distribution (MRSD) with improved ripple size for LT codes[J]. IEEE Communications Letters, 2013, 17(5): 976-979.

[8] ZENG M, CALDERBANK R, CUI S. On design of rateless codes over dying binary erasure channel[J]. IEEE Trans.on Communications, 2012, 60(4): 889-894.

[9] HAYAJNEH K F, YOUSEFI S, VALIPOUR M. Improved finite-length Luby-transform codes in the binary erasure channel[J]. IET Communications, 2015, 9(8): 1122-1130.

[10] LIAO J, ZHANG L, LI T, et al. Design of optimised multiple partial recovery LT codes[J].IET Communications,2016,10(9):1053-1062.

[11] AREF V. Rateless codes from spatially coupled regular-LT codes[C]∥Proc.of the IEEE Workshop on Communication and Information Theory, 2015: 1-6.

[12] 陈英,顾术实,焦健,等.基于无码率码的独立窗不等差错保护方案[J]. 系统工程与电子技术,2014,36(5):991-996.

CHEN Y, GU S S, JIAO J, et al. Independent window UEP scheme based on rateless codes[J]. Systems Engineering and Electronics, 2014, 36(5):991-996.

[13] 赵旦峰,司佳希,梁明珅,等. 基于算术编码的低冗余LT码及其在安全通信中的应用[J]. 系统工程与电子技术,2016,38(2):409-414.

ZHAO D F, SI J X, LIANG M S, et al. Low redundancy LT code based on arithmetic coding and its application in secure communication[J]. Systems Engineering and Electronics,2016, 38(2):409-414.

[14] YAO W Q, YI B S, HUANG T Q, et al. Poisson robust soliton distribution for LT codes[J]. IEEE Communications Letters, 2016, 20(8): 1499-1502.

[15] ETESAMI O, SHOKROLLAHI A. Raptor codes on binary memoryless symmetric channels[J]. IEEE Trans.on Information Theory, 2006, 52(5): 2033-2051.