基于联合局域相关向量机的雷达导引头状态预测方法

逯 程, 徐廷学, 王 虹

(1. 海军航空大学岸防兵学院, 山东 烟台 264001; 2. 中央军委联合参谋部第55研究所, 北京 100094)

0 引 言

状态预测技术是视情维修(condition based maintenance, CBM)策略的关键技术之一,它通过整合装备当前及历史状态监测数据,判断其在未来一段时间内的状态发展趋势,从而为维修保障提供决策信息。

目前,装备的退化状态预测方法主要分为3类[1]:基于经验、基于模型和基于数据驱动的预测。基于经验的预测方法通常针对状态信息获取困难的装备,该方法实现简单,但是预测结果往往不够理想;基于模型的预测方法需要对装备状态进行精确的数学建模,而这一点对于复杂的机电装备难度较大;而基于数据驱动的预测方法[2-4]灵活性较强,适用于各类型装备的退化状态预测,具有很可观的工程实用价值。当前,人工神经网络(artificial neural network, ANN)、灰色系统理论(grey system theory, GST)和支持向量机(support vector machine, SVM)已被广泛用于这一领域的研究,并表现出不错的性能。但它们也存在一些固有缺陷,如ANN在优化过程中易陷入局部最优值,且性能受到训练样本量的限制;GST极易受到数据序列波动性的影响,且长期预测精度不佳;SVM模型参数设置复杂,稀疏性有限,输出结果没有概率输出,忽视了预测的不确定性问题。这些不足极大限制了它们在工程上的实际应用。

相关向量机(relevance vector machine, RVM)是文献[5-6]于2001年提出的一种基于稀疏Bayesian学习理论的机器学习算法。与SVM相比,其核函数不受Mercer条件的限制,选取更加灵活;参数设置简单,避免了复杂的附加参数;解的稀疏性也远高于SVM,具有较好的泛化能力;其概率式的输出也能有效提供更多决策信息,降低预测风险[5-6]。目前,已在寿命预测[7]、可靠性预测[8]及时间序列预测[9]等领域取得了不错的应用效果,是当前小样本预测建模问题的研究热点。

所以本文结合装备保障实际,在RVM回归模型的基础上,提出了一种基于联合局域相关向量机(united local relevance vector machine, U-LRVM)的预测方法。通过构建一种方差高斯核函数来提高核函数的全局性能和泛化能力;通过借鉴混沌序列局域预测法中邻近点个数的选取方法,利用Hannan-Quinn(H-Q)准则对训练空间预测嵌入维数进行优化,避免了主观选取的盲目性,完成了改进局域相关向量机(local relevance vector machine, LRVM)模型的构建;针对传统预测方法仅考虑单一性能指标变化趋势的不足,利用具有近似退化规律的同源装备测试数据对LRVM进行了改进,结合Dempster-Shafer (D-S)证据理论在数据融合领域的优良性能,对传统和改进LRVM两种模型进行了融合,建立了U-LRVM模型,如图1所示。

图1 U-LRVM 预测模型Fig.1 Prediction model of U-LRVM

1 RVM预测模型

1.1 RVM回归原理

RVM是一种非线性稀疏Bayesian学习理论,其良好的泛化性能和较少的相关向量使其在预测领域取得了较好的应用,其回归模型原理如下。

ti=y(xi,ω)+εi

(1)

式中,样本高斯噪声εi～N(0,σ2)。类似于SVM的表达式,将式(1)用一系列核函数可以表示为

(2)

式中,ω=[ω0,ω1,…,ωN]T为权参数向量;K(·,·)为核函数。因此可以推断出p(ti|xi)=N(ti|y(xi,ω),σ2),即ti满足ti～N(y(xi,ω),σ2)。为方便表达,引入超参数β=σ-2,则整个训练样本数据组的似然函数表示为

(3)

式中,t=[t1,t2,…,tN]T;Φ∈RN×(N+1)是设计矩阵,定义为Φ=[φ(x1),φ(x2),…,φ(xN)]T,基函数向量。

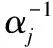
(4)

式中,在超参数α=[α1,α2,…,αN]中的每个αj都相互独立且只与对应的权值ωj相关。利用式(3)和式(4),根据Bayesian公式即可得到ω后验分布的均值矩阵μ和协方差矩阵Σ分别为

Σ=(βΦTΦ+A)-1

(5)

μ=βΣΦTt

(6)

式中,Α=diag(α0,α1,…,αN)。若要得到ω的后验分布,必须对两个影响参数β和αj进行优化,具体方法为最大化边缘似然函数p(t|α,β)。对p(t|α,β)等号两边取对数得到目标函数后,再根据目标函数分别对αj和β求偏导并令导数为0,得到两个参数的迭代计算公式为

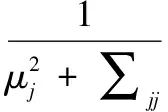
(7)

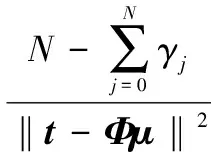
(8)

γj=1-αjΣjj

(9)

式中,μj为μ的第j个元素;Σjj是协方差矩阵Σ第j个对角元。

y*=μTφ(x*)

(10)

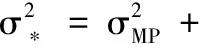
(11)

1.2 RVM预测置信区间计算

(12)

若置信度设为1-θ,则

(13)

式(13)即p{y*-σ*zθ/2,y*-σ*zθ/2}=1-θ,所以t*置信度为1-θ的双侧置信区间为[y*-σ*zθ/2,y*-σ*zθ/2],上位数zθ/2可以通过标准正态分布表查找获取。

2 RVM回归模型参数优化

2.1 高斯核函数的改进

通过在SVM基础上把基于高斯过程中的Bayesian推理应用到核理论上,RVM算法在先验参数的结构下利用自相关判定理论(automatic relevance determination, ARD)移除不相关的样本点,从而实现了模型的稀疏化[10]。虽然与SVM相比,RVM的核函数由于稀疏、较少的超参数而计算量大减,且脱离了Mercer条件的限制,但是预先确定的核函数性能依然会直接影响到RVM回归预测的精度。

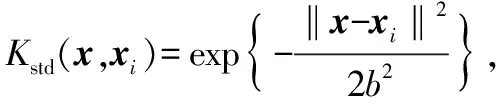
作为一种基于距离方程的核函数,高斯核函数的测试点在由源空间映射到高维特征空间后往往会变得稀疏。只有当核函数不仅能在测试点保持较快的衰减,而且在无限远处也能保持一定的衰减时,上述情况才能得到改变。然而,高斯核函数只满足前者,所以它是一种典型的局部核函数。近年来,很多学者通过构造高斯核函数与全局性核函数组成的混合核来提高核函数的性能[11-16],但在这个过程中又引入了多个参数变量,大大增加了RVM的计算复杂度。本文在高斯核函数的基础上,通过构造一种改进的方差高斯核函数来提高RVM的性能。

在高斯核函数的标准形式里,所有的特征元素都利用相同的尺度因子来衡量,这一特性也使得具有大数值尺度范围的特征要更占优势,这一局限性也严重影响了其在实用中的性能。为克服这一问题,使各特征元素进行零均值归一化并将其标为单位标准差形式，即

(14)

式中,μi和σi是特征向量的均值与标准差。将式(14)代入标准形式,将得到的结果改写成核函数的形式,就产生了一个新的核函数,即

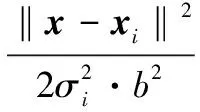
(15)

(16)

这样构造的核函数不仅满足前文提到的两个条件,而且成功避免了未知参数的引入,另外在模型数据的输入前也不需要数据的归一化过程。文献[17]中的研究指出,调整唯一的带宽参数b对提高核函数的性能效果并不明显,可以视为正态分布中的标准差σ。

2.2 训练样本空间维数的优化

实现时间序列{x1,x2,…,xn}预测的关键在于寻找到滑动时间窗口Xt={xt-1,xt-2,…,xt-m}与输出Yt={Xt}之间的准确映射f:Rm→R,其中,t=m+1,m+2,…,n,m为预测嵌入维数。因此,参数m的确定对于预测建模的准确性至关重要。为了克服m选取的主观盲目性,本文基于混沌时序的局域预测法[18-19]中邻近点个数选取的思想,对RVM的训练样本空间最优嵌入维数进行了优化,该方法适合小数据量的情况,具有计算简单和精度高的特点。

在邻近点个数的确定过程中,本文基于H-Q准则[23],过程如下:

对d给定一个宽泛的范围d∈[dmin,dmax],依次计算每个d值下的H-Q准则值:

(17)

(18)

3 基于数据融合的U-LRVM预测模型

3.1 联合相关向量机思想

导弹在进行末制导雷达单元测试后,会得到雷达多个指标的性能测试数据。传统采用RVM对性能参数进行预测是通过该参数的历史测试数据预测其未来时刻的状态参数值,但这种预测模型太过单一,预测结果也并不能十分令人信服。考虑到在导弹的实际贮存过程中,每季度正常情况下往往会对同批次的多个导弹同时进行检测维护,这些同一生产批次导弹来自相同的工业生产厂家,统一列装部队后一直处于相同的贮存环境下,每次进行导弹贮存检测时都会有数枚弹一起参与测试并记录数据,也就是说，它们具有同源相近性的特点,本文统一称其为同源装备。所以，同源导弹往往具有相同的状态退化规律,即其他导弹的性能参数变化也能从一定程度上反映待预测导弹的某一性能参数变化情况。基于以上分析,为充分利用同源导弹的性能退化数据,提出了一种联合相关向量机(united relevance vector machine, U-RVM)的预测模型。

图2 U-RVM 预测模型Fig.2 Prediction model of U-RVM

3.2 D-S证据组合规则

证据融合规则可以使来自不同信息源的证据融合成为更准确可靠的信息,也是D-S证据理论的核心[25]。Dempster证据组合规则如下:设Bel1和Bel2是识别框架U上的两个信度函数,m1和m2分别是其对应的基本概率赋值(basic probability assignment,BPA),焦元分别为A1,…,Ak和B1,…,Br,则有

(19)

3.3 BPA的选取

在预测问题中,以第3.1节提到的两种模型构建识别框架U={f1,f2},若它们进行q次预测则产生证据集E=(e1,e2,…,eq),mk(fj)为第k(k=1,2,…,q)次预测后证据ek对P-RVM或C-RVM预测模型的信任程度,即对第j(j=1,2)种模型的BPA值。本文基于模型预测效果的思想设计BPA计算公式,当模型预测偏差较大时,相对应的BPA值也会越小,基于这一原则,具体计算方法为

(20)

mk(U)=0

(21)

(22)

在预测过程中,基于新陈代谢的思想,每次产生的新证据会与之前的证据进行动态融合,有效增强了模型对新信息的适应能力和利用率。

3.4 权重系数的确定

根据P-RVM和C-RVM的组合模型U-RVM在t+1时刻对性能参数vi进行预测:

(23)

从式(23)可以看出,权重的分配将是影响U-RVM预测结果的关键因素。传统的基于专家经验的权重分配方式具有很大的主观盲目性,所以本文利用D-S证据理论能够根据证据累加来处理不确定性因素的优点,通过证据集的融合处理进行权重分配,具体计算方法为

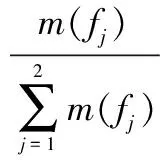
(24)

式中,ωk,j为第k次预测后第j种模型所分配的权重值;m(fj)为证据融合后的第j种模型的BPA值。

3.5 U-LRVM预测算法

将改进的LRVM算法与U-RVM算法进行结合,构成了本文设计的U-LRVM算法,具体步骤如下。

步骤1确定某装备待预测的I种性能指标,给定某性能指标测试序列vi=(vi,1,vi,2,…,vi,N),1≤i≤I,vi,j为j(1≤j≤N)时刻的参数值。同时确定p个同源测试装备的性能指标矩阵

步骤2设定预测步数q。对P-RVM模型,训练数据进行相空间重构得

C-LRVM重构后的训练数据为

步骤5利用式(19)计算本次预测与之前预测的模型融合BPA值。

步骤6对之前的预测步数k进行判断。若达到，则利用式(24)计算得到组合预测模型的权重ωk,j；否则返回步骤4继续下一步预测。

U-LRVM预测算法的流程图如图3所示。

图3 U-RVM算法流程图Fig.3 Flow chart of U-RVM algorithm

4 实例分析

雷达导引头是导弹武器系统中最为复杂的关键设备之一,其性能状态的优劣直接影响到导弹的作战效能能否正常发挥,因而对其进行状态预测是十分必要的。

以某岸导团面向贮存任务的一批同源导弹为基础,选取某导弹雷达导引头为预测研究对象。通过对导弹定期按季度进行雷达单元测试,从2009年初至2016年9月,获得4个关键参数的31组数据,如表1所示。本文限于篇幅,表中只列出了部分数据,同源装备测试数据没有列出。表1中前28组数据用于训练学习,2016年的3组数据用于检验预测效果。

表1 关键指标参数测试数据

确定训练嵌入维数m=3后,将训练预测次数设定为2,运用前28组数据对P-LRVM和C-LRVM进行训练预测,将预测结果代入式(20)、式(21),得到每次预测时两种模型的BPA,进一步利用式(19)得到预测结束后二者的融合BPA值,将其代入式(24),得到U-LRVM中P-LRVM和C-LRVM模型的权重分配,如表2所示。

表2 权重的分配

为验证本文所提预测方法的有效性,针对雷达导引头的4个关键指标分别运用5折交叉验证的最小二乘支持向量机(least squares-support vector machine,LS-SVM)、RVM和本文提出的U-LRVM方法进行预测,预测结果如图4～图7所示。

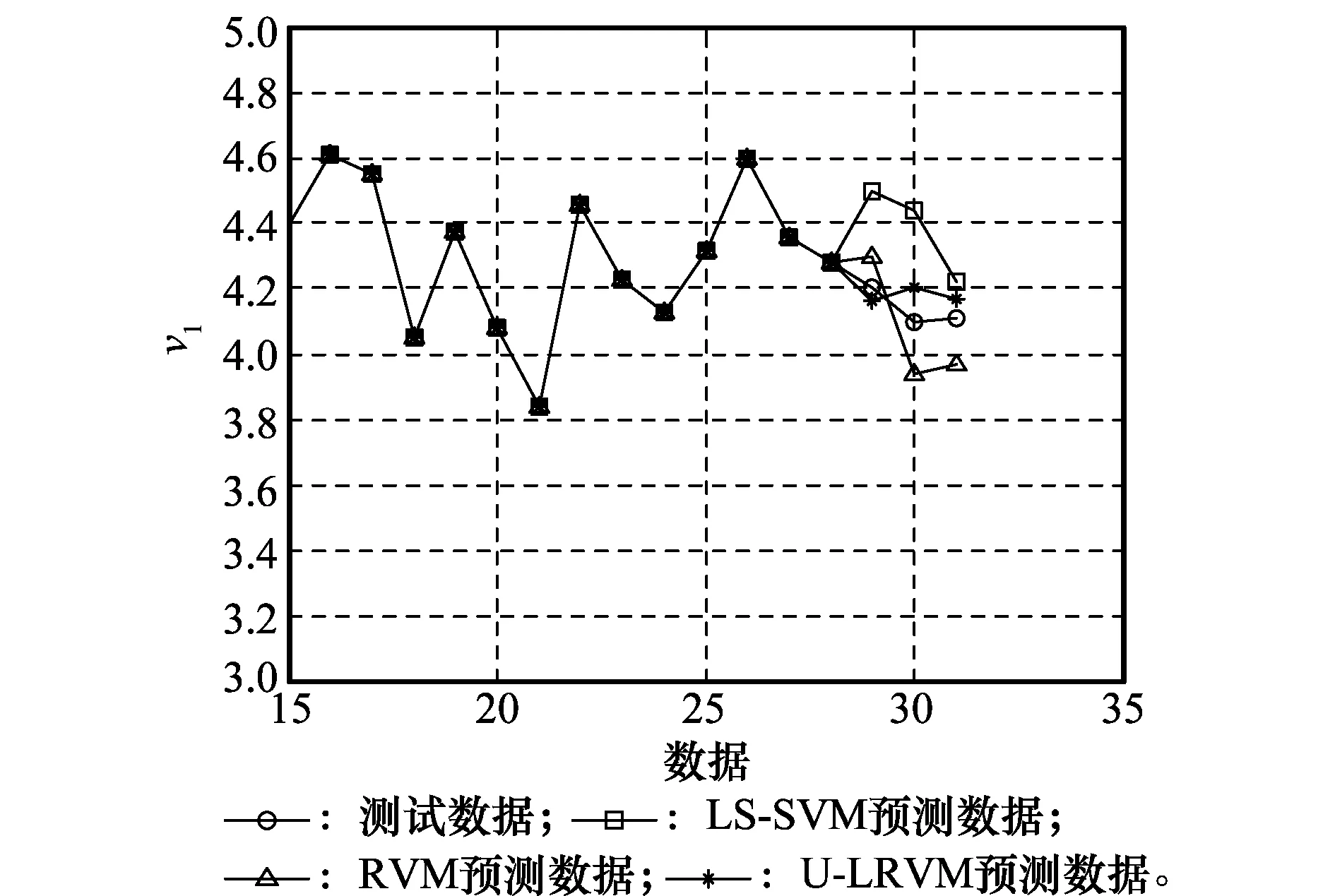
图4 参数v1的预测曲线Fig.4 Prediction curves of parameter v1

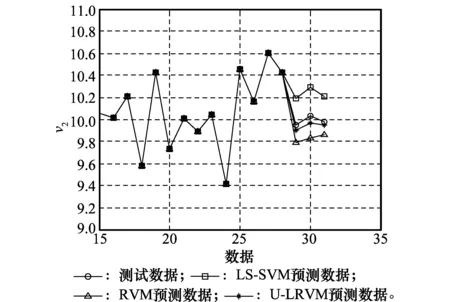
图5 参数v2的预测曲线Fig.5 Prediction curves of parameter v2

为了更直观地观察最后3组数据的预测效果,图4～图7的横坐标从第15组数据开始选取,可以明显看出,针对各关键指标的预测,RVM的性能都要优于LS-SVM,这说明在预测回归领域,RVM是一种比LS-SVM更为先进的智能学习算法。而通过对RVM进行改进并融合同源装备的信息后,U-LRVM较传统RVM取得了更佳的预测效果。为进一步对各方法的预测精度准确地进行分析,采用平均绝对百分比误差(mean absolute percentage error, MAPE)作为预测性能评价指标,该指标避免了求和时的正负抵消问题,且不受量纲的影响,其结果如表3所示。

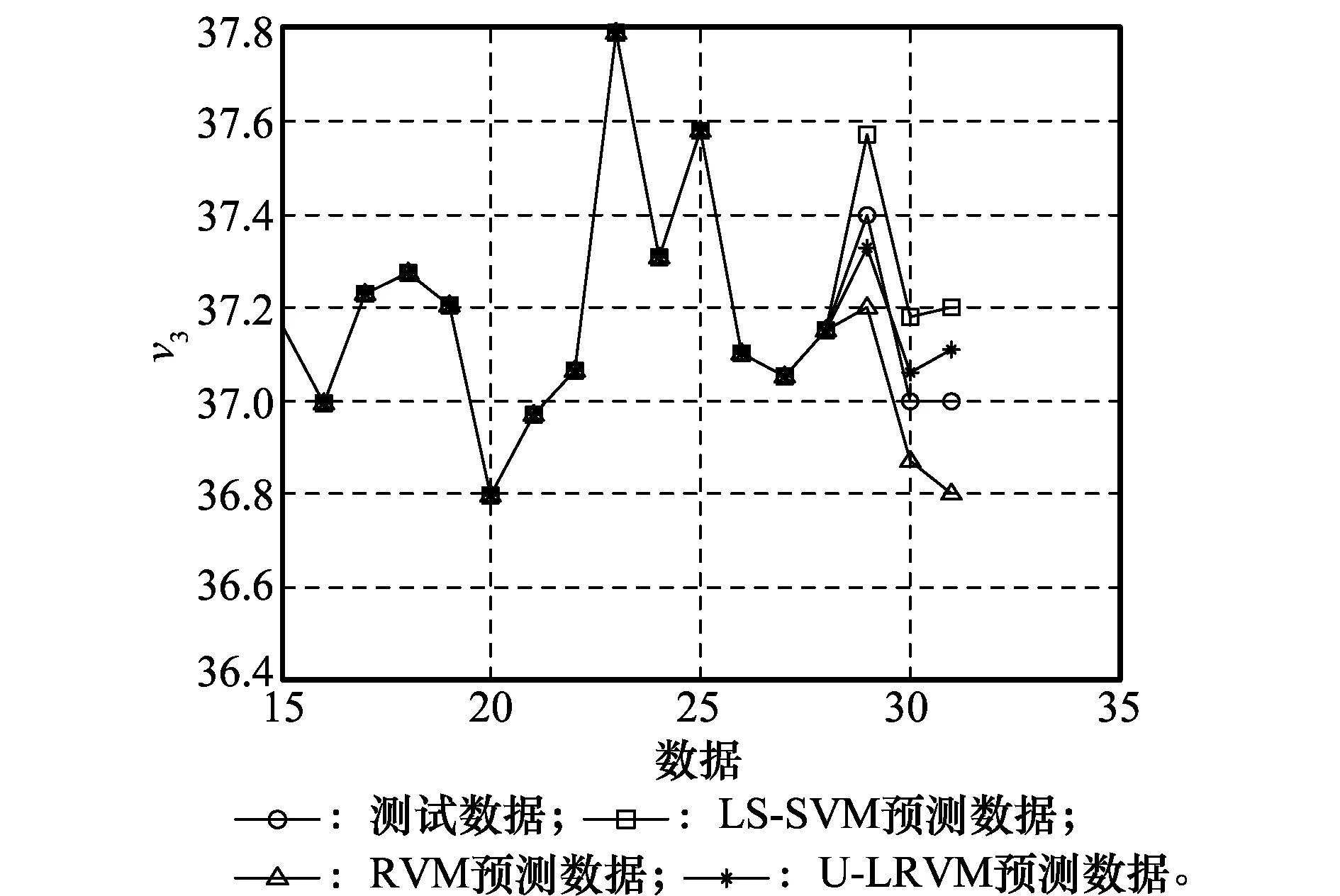
图6 参数v3的预测曲线Fig.6 Prediction curves of parameter v3

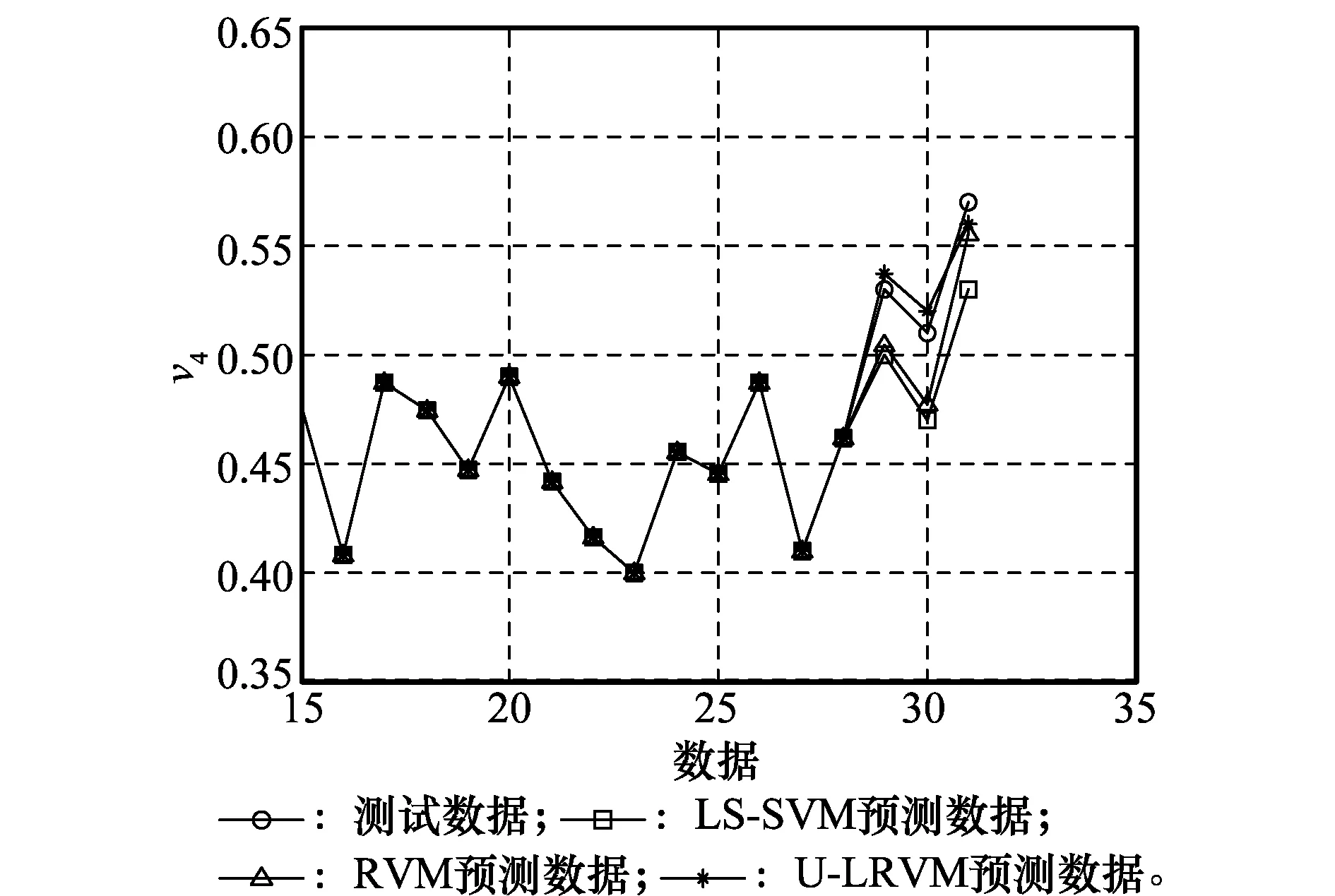
图7 参数v4的预测曲线Fig.7 Prediction curves of parameter v4

由表3可知,针对各状态参数的预测,U-LRVM的结果MAPE都比另外两种方法要低,这说明其预测精度显著高于另外两种方法,从而验证了该预测方法的有效性和优越性。本文设计的U-LRVM模型并没有忽略同源装备信息,具有较好的动态融合性,且计算简便,有很好的工程应用前景。

下面结合预测值的置信区间讨论U-LRVM方法概率式预测的意义。图8为4个指标的预测值与其置信度为90%和95%的置信区间。

从图8中可以看出,指标的测试真实值均落于置信度为95%的区间内,且预测值与参数实际变化趋势也较为一致。针对点预测可能由于不可靠的预测结果而导致欠维修或过维修的严重后果,这种概率式的输出可以有效规避确定性预测风险,为未来雷达导引头健康状态的评估及后续的维修保障决策提供更为合理有效的判断。

图8 各参数的预测值及置信区间Fig.8 Predicted value and the confidence interval of each parameter

5 结束语

通过对雷达导引头关键指标进行准确地预测可以合理计划和优化维修活动,实现导弹的精细化保障目标。在分析当前状态预测技术和相关向量机理论发展的基础上,本文提出了U-RVM模型的雷达导引头装备状态预测方法。通过设计一种新的高斯方差核函数和优化预测训练嵌入维数来增强RVM的泛化能力和非线性拟合能力,构建了LRVM模型。在此基础上,通过D-S证据理论对P-LRVM和C-LRVM模型的预测结果进行了融合,建立了U-LRVM模型。该模型充分利用了具有近似退化特性的同源关联装备丰富的检测信息,基于客观预测误差动态确定模型权重,有效避免了人为因素的干扰。实例分析结果表明,该预测方法精度更高,计算简便,且概率式的输出结果可以为装备健康状态评估提供更为可靠的判断,其应用前景十分广阔。

[1] 赵建忠,欧阳中辉,张磊,等.基于多智能体遗传算法优化的航空电子设备状态组合预测[J].兵工学报,2016,37(4): 727-734.

ZHAO J Z, OUYANG Z H, ZHANG L, et al. Combined prediction on avionics state opimized by MAGA[J]. Acta Armamentarii, 2016, 37(4): 727-734.

[2] 李颖峰. 改进灰色模型在电力负荷预测中的应用[J]. 电网与清洁能源, 2009, 25(3):10-11.

LI Y F. The application of improved grey model in power system load forecast[J].Power System and Clean Energy,2009,25(3):10-11.

[3] DONG Q L. Application of support vector machine regression method in prediction of ship’s price index[J]. Ship & Ocean Engineering, 2009, 38(2): 104-106.

[4] 朱建平. 神经网络在电力负荷预测中的应用研究[J]. 科技资讯, 2015, 13(23): 32-34.

ZHU J P. Research on application of neural network in power load forecasting[J]. Science and Technology Information, 2015, 13 (23): 32-34.

[5] TIPPING M E. Sparse Bayesian learning and the relevance vector machine[J]. Journal of Machine Learning Research,2001,1: 211-244.

[6] SAMUI P, DIXON B. Application of support vector machine and relevance vector machine to determine evaporative losses in reservoirs[J].Hydrological Processes,2012,26(9):1361-1369.

[7] 雷亚国, 陈吴, 李乃鹏,等. 自适应多核组合相关向量机预测方法及其在机械设备剩余寿命预测中的应用[J]. 机械工程学报, 2016, 52(1):87-93.

LEI Y G, CHEN W, LI N P, et al. Adaptive multi kernel combined correlation vector machine prediction method and its application in prediction of residual life of mechanical equipment[J]. Journal of Mechanical Engineering, 2016, 52(1): 87-93.

[8] 冯鹏飞, 朱永生, 王培功,等. 基于相关向量机模型的设备运行可靠性预测[J]. 振动与冲击, 2017, 36(12):146-149.

FENG P F, ZHU Y S, WANG P G, et al. Reliability prediction of equipment based on correlation vector machine model [J]. Vibration and Shock, 2017, 36(12): 146-149.

[9] 范庚,马登武,吴明辉,等.电子系统状态时间序列预测的优化相关向量机方法[J].系统工程与电子技术,2013,35(9):2011-2015.

FAN G, MA D W, WU M H, et al. Optimized correlation vector machine method for prediction of state time series of electronic systems[J].Systems Engineering and Electronics,2013,35(9): 2011-2015.

[10] 周建宝. 基于 RVM 的锂离子电池剩余寿命预测方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2013.

ZHOU J B. Research on prediction method of remaining life of lithium ion battery based on RVM[D]. Harbin: Harbin Institute of Technology, 2013.

[11] YU J. A nonlinear kernel Gaussian mixture model based inferential monitoring approach for fault detection and diagnosis of chemical processes[J]. Chemical Engineering Science, 2012, 68(1): 506-519.

[12] WEI L, WEI B, WANG B. Text classification using support vector machine with mixture of kernel[J]. Journal of Software Engineering and Applications, 2013, 5(12): 55-58.

[13] MIAO S, XIE K, YANG H, et al. A mixture kernel density model for wind speed probability distribution estimation[J]. Energy Conversion and Management, 2016, 126: 1066-1083.

[14] LIU K H, LIN Y Y, CHEN C S. Linear spectral mixture analysis via multiple-kernel learning for hyperspectral image classification[J]. IEEE Trans.on Geoscience and Remote Sensing, 2015, 53(4): 2254-2269.

[15] YU J, CHEN K, MORI J, et al. A Gaussian mixture copula model based localized Gaussian process regression approach for long-term wind speed prediction[J].Energy,2013,61(6):673-686.

[16] OHISHI Y, MOCHIHASHI D, KAMEOKA H, et al. Mixture of Gaussian process experts for predicting sung melodic contour with expressive dynamic fluctuations[C]∥Proc.of the IEEE International Conference on Acoustics, Speech and Signal Processing, 2014: 3714-3718.

[17] REMAKI L, CHERIET M. KCS-new kernel family with compact support in scale space: formulation and impact[J]. IEEE Trans.on Image Processing, 2000, 9(6): 970-981.

[18] LI H C, ZHANG J S. Local prediction of chaotic time series based on support vector machine[J]. Chinese Physics Letters, 2005, 22(11): 2776-2779.

[19] 杜杰,曹一家,刘志坚,等.混沌时间序列的局域高阶Volterra滤波器多步预测模型[J].物理学报,2009,58(9):5997-6005.

DU J, CAO Y J, LIU Z J, et al. A multi-step prediction model of local high order Volterra filters with chaotic time series[J]. Acta Physica Sinica, 2009, 58(9): 5997-6005.

[20] MENG Q F, CHEN Y H, FENG Y H. Small-time scale network traffic prediction based on a local support vector machine regression model[J]. Chinese Physics B, 2009, 18(6): 2194-2199.

[21] BING Q, GONG B, YANG Z, et al. Short-term traffic flow local prediction based on combined kernel function relevance vector machine model[J]. Mathematical Problems in Engineering, 2015, 154703: 1-9.

[22] MENG Q F, CHEN Y H, FENG Y H, et al. Nonlinear prediction of small scale network traffic based on local relevance vector machine regression model[J]. Acta Physica Sinica, 2013,62(15):150-189.

[23] HANNAN E J, QUINN B G. The determination of the order of an autoregression[J].Journal of the Royal Statistical Society, Series B (Methodological), 1979，41(2): 190-195.

[24] 孟庆芳, 彭玉华, 曲怀敬, 等. 基于信息准则的局域预测法邻近点的选取方法[J]. 物理学报, 2008, 57(3): 1423-1430.

MENG Q F, PENG Y H, QU H J, et al. Local information criterion prediction selection method based on the adjacent point[J]. Acta Physisc Sinica, 2008, 57 (3): 1423-1430.

[25] 苏晓燕. 关联证据融合研究[D]. 上海:上海交通大学, 2014.

SU X Y. Study on correlation evidence fusion[D]. Shanghai: Shanghai Jiaotong University, 2014.