基于改进型PASTd双基地MIMO雷达角度跟踪算法
张正言, 张剑云
(国防科技大学电子对抗学院, 安徽 合肥 230037)
0 引 言
随着战场环境的日益复杂,传统雷达性能难以充分发挥,越来越难以适应战争需求。因此近年来越来越多的新体制雷达被提出,多输入多输出(multiple input multiple output, MIMO)雷达是新体制雷达中的典型代表,引起了众多研究机构和学者的重点关注,公开发表了大量的研究成果。MIMO雷达有多个发射和多个接收雷达,发射雷达发射相互正交的信号,经目标反射后到达接收雷达,经过匹配滤波器后得到了多个路径的信号。MIMO雷达充分利用了多个传感器的优势,与经典的相控阵雷达不同,MIMO雷达能够明显地提高目标检测、定位、跟踪等性能[1-5]。双基地MIMO雷达在MIMO雷达体制中工程实现性最强,因此本文针对双基地MIMO雷达展开研究。双基地MIMO雷达是通过估计目标的发射角度(direction of departure, DOD)和接收角度(direction of arrival, DOA)来确定目标位置,因此有大量关于双基地MIMO雷达收发角度估计的算法[6-13]。
上述算法都是针对静止目标收发角度的估计,需要大量的快拍数据,并且复杂度较高,当目标运动时,每个快拍数据对应的目标角度不同,因此上述算法性能急剧下降甚至失效。实际战场环境中,目标往往不是静止的,运动目标相邻时刻角度是相关的,相应的接收数据对应的角度不同,因此角度估计算法无法解决跟踪问题,成为制约双基地MIMO雷达实际应用的关键问题。目前公开发表跟踪方面的文献多是关于统计MIMO雷达的,而双基地MIMO雷达跟踪问题研究还较少,仍然没有得到很好的解决。
关于MIMO雷达跟踪方面的公开发表的文献较少,文献[14]中给出的单基地MIMO雷达跟踪算法,算法复杂度较低,但是代价是跟踪性能的降低。文献[15]将Kalman引入到紧缩投影近似子空间跟踪(projection approximation subspace tracking deflation, PASTd)算法,用Kalman滤波技术实现数据相关,并且算法收敛速度快。上述文献都是关于单基地MIMO雷达目标跟踪问题。
双基地MIMO雷达与单基地MIMO雷达不同,由收发基地组成,对应的接收角和发射角不相等,因此联合导向矢量更加复杂,上述文献算法无法解决双基地MIMO雷达目标跟踪问题。文献[16]针对地面干扰源定位问题,建立了新的信号模型,利用分数阶模糊函数峰值点搜索实现速度估计,结合投影近似子空间跟踪(projection approximation subspace tracking, PAST)算法实现对飞机运动状态的实时估计,但是算法不具有一般性。文献[17]推导了相邻时刻协方差矩阵差公式,从中提取与角度差的关系式,进而实现目标角度跟踪。该算法计算量小,但跟踪性能差。文献[18]提出了基于自适应非对称联合对角化(adaptive asymmetric joint diagonalization, AAJD)目标角度跟踪算法。算法不需要额外的关联算法,但是求解角度时利用了上一时刻的估计角度,降低了算法的性能。
文献[19]将阵列信号中的PASTd算法引入到双基地MIMO雷达,成功解决了双基地MIMO雷达目标跟踪问题。该算法跟踪性能优于文献[17]和文献[18],但需要额外的数据相关运算,并且不能跟踪相同收发角的目标。
因此本文针对文献[19]存在的问题,提出了相邻时刻收发角度自动关联算法,同时实现了收发角度自动配对,利用估计出的目标收发角度,得到收发导向矢量,作为下一时刻跟踪寻优算法的初始矢量,因此能够成功跟踪相同接收角或发射角的目标。
1 信号模型
本文用双基地MIMO雷达观察空中运动目标,目标与基地距离较远,符合点目标模型。双基地MIMO雷达有M个发射阵元和N个接收阵元组成,收发阵元平均分布,间隔相同且为波长λ的一半。双基地MIMO雷达的配置如图1所示。

图1 双基地MIMO雷达收发阵元配置Fig.1 Bistatic MIMO radar transceiver element configuration

假设第m个发射阵元的发射窄带正交信号为sm(t)·exp(j2πfct),sm(t)为基带信号,fc为载波的频率。m个发射阵元发射的信号辐射到P个目标,散射后到达接收阵元的信号为

(1)
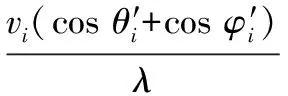
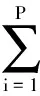
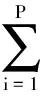
(2)
式中,εiexp(jωit)与εi的统计特性相同,ε=[ε1exp(jω1t),…,εPexp(jωPt)]T仍满足SwerlingⅡ模型;n(t)均值为零,协方差矩阵为σ2IMN。
进一步简化式(2)得
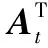
(3)
对式(3)进行取直操作
x(t)=At(φ)⊙Ar(θ)vec(diag(ε))+n(t)=
W(φ,θ)ε+n(t)
(4)
式中,W(φ,θ)=[at(φt,1)⊗ar(θt,1),at(φt,2)⊗ar(θt,2),…,at(φt,P)⊗ar(θt,P)]为MN×P维的收发方向矢量;⊙和⊗分别代表Khatri-Rao积和Kronecker积。
2 算法描述
PASTd算法通过求解目标函数最小值求出估计特征矢量,结合旋转不变子空间(estimation of signal parameters via invariance techniques, ESPRIT)算法估计出目标收发角度。PASTd算法的计算复杂度低,估计精度能满足跟踪要求。但是算法不能实现角度自动关联,且当目标发射角或接收角相同时,算法将失效。
改进PASTd算法在原算法的基础上,通过PASTd算法的求优过程,估计出目标的特征矢量,然后增加目标角度的关联算法,关联算法同时实现了同一目标收发角度的自动配对。通过目标角度自动关联配对算法估计出此时的目标角度,利用得到的目标收发角度,代入收发导向矢量公式,得到准确的收发导向矢量,替代求优过程估计出的特征矢量,作为下一时刻求优过程的初始矢量。
因此,改进PASTd算法将跟踪过程分为两步,第一步通过目标函数寻优算法估计出目标特征矢量,第二步利用得到的特征矢量结合自动关联配对算法,实现对目标角度的估计,配对及关联运算,然后求出收发导向矢量,值得注意的是求出的收发导向矢量比第一步估计出的特征矢量更接近真实方向矢量,并且满足收发导向矢量的标准形式,因此用来更新特征矢量,作为下一时刻跟踪算法的初始矢量。
文献[20]指出PASTd算法的基础是投影降维,每一次循环迭代相当于对一个目标的收发导向矢量进行更新,从而完成跟踪过程。本文中的改进PASTd算法t时刻的初始矢量是通过t-1时刻算法步骤2得到的,即特征矢量的每一列对应于一个目标,因此经过PASTd算法求出的特征矢量的每一列也对应于一个目标。
2.1 特征矢量的估计
改进PASTd算法的最小目标函数与PASTd算法的最小目标函数相同[20],其表达式为
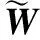
(5)
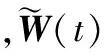
(6)
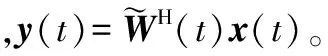

(7)

(8)

(9)

y(t)=WH(t-1)x(t)
(10)
y(t)=W-1(t-1)x(t)
(11)
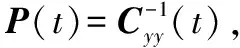
(12)

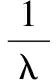
(13)
然后给出估计误差
e(t)=x(t)-W(t-1)y(t)
(14)
由递归最小二乘法可得特征矢量的更新,即
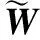
(15)
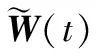
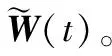
2.2 目标收发角度的估计、配对及相关算法
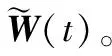
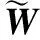
(16)
此时,存在一个唯一的非奇异矩阵T(t),使得
(17)
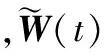
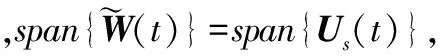
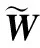
(18)
式(18)等式两边同时乘以y(t)得
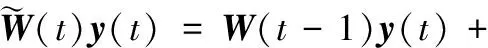

(19)
为了表达方便,令α=yH(t)PH(t-1)y(t),简化式(19)得
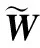
(20)
进一步化简得
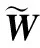
(21)
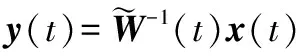
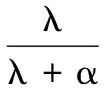
(22)
化简得
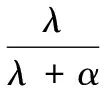
(23)
对比式(23)两边可以得出
(24)
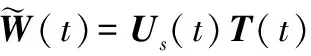
Us(t)T(t)=Us(t-1)T(t-1)
(25)
PASTd算法假设相邻时刻角度变化较少,即Us(t)≃Us(t-1)代入式(25)得
T(t)=T(t-1)=T
(26)
W(t-1)是t-1时刻改进PASTd算法第二步得到的收发导向矢量,则W(t-1)与Us(t-1)仅仅是经过列变换,经过t时刻跟踪算法得到W(t),不改变列的顺序,W(t)与W(t-1)两个矩阵每一列都对应一个相同的目标。由此可知T=QE,Q为比例因子矩阵,E为列交换矩阵。
证毕
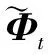
值得注意的是当t=1时,命题一不成立,因此本文算法在t=1直接利用ESPRIT算法估计角度,确定估计目标角度的顺序。
下面给出目标收发角度自动关联配对算法。
Ift==1
对Ψr进行特征值分解:Ψr=TΦrT-1
取Φr的对角线元素组成ωr
取Φt的对角线元素组成ωt
Else
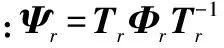
令Tr每一行的最大值为1,其余元素为零,得到了Er


令Tt每一行的最大值为1,其余元素为0,得到Et
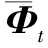
End
2.3 特征矢量的更新
根据第2.2节的算法得到包含角度信息的矩阵ωr和ωt,利用公式
求出θ(t),φ(t)。将其代入收发导向矢量公式得
at(φt,i)=[1,ejπsin φt,i…,ejπ(M-1)sin φt,i]
(27)
ar(θt,i)=[1,ejπsin θt,i,…,ejπ(N-1)sin θt,i]
(28)
W(t)=[at(φt,1)⊗ar(θt,1),…,at(φt,P)⊗ar(θt,P)]
(29)
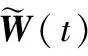

表1 改进PASTd算法流程
3 实验仿真及结果分析
双基地MIMO雷达收发阵元间距为波长的一半,采用高斯白噪声。发射信号的载波频率为1 GHz,脉冲重复频率为10 kHz,脉冲宽度为10 ms,发射信号为哈达码脉冲信号。
定义
RMSE(θ)=
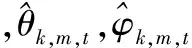
实验1验证算法有效性
首先对比PASTd算法和改进PASTd算法定位固定目标,验证算法的有效性及优势。假设空中有4个感兴趣的点目标,目标为静止目标,收发阵元数M=N=3,信噪比(signal-to-noise ratio, SNR)SNR=10 dB 时,遗忘因子λ=0.95。4个目标的位置为(θ1,φ1)=(30°,-40°),(θ2,φ2)=(40°,20°),(θ3,φ3)=(-50°,30°)和(θ4,φ4)=(-20°,-10°),所有目标的收发角度都不相同,仿真定位结果如图2所示。4个目标的位置为(θ1,φ1)=(30°,-40°),(θ2,φ2)=(40°,20°),(θ3,φ3)=(-50°,20°)和(θ4,φ4)=(-50°,-20°),目标三的收发角分别与目标二发射角、接收角相同,定位结果如图3所示。
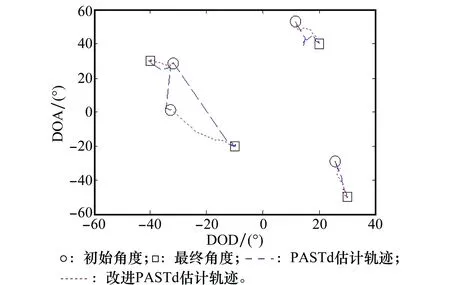
图2 算法定位收发角度不同目标结果Fig.2 Positioning results of target of different Transceiver angle

图3 算法定位收发角度相同目标结果Fig.3 Positioning results of target of same Transceiver angle
从图2可以看出,PASTd算法与改进PASTd算法最后的估计角度与真实角度相同,说明两种算法的有效性,当目标收发角度都不同时能够成功定位目标。但是改进PASTd算法估计轨迹近似成直线,收敛速度较快,而PASTd算法估计轨迹分散,收敛速度慢,这是因为改进PASTd算法增加步骤2,更新了估计的特征矢量并作为下一时刻的初始矢量。从图3仿真结果可以看出,改进PASTd算法仍然有效,而PASTd算法已经失效,不能成功定位相同角度的目标,验证了理论的有效性。
设空中有5个运动点目标,目标为非匀速运动并且相互独立,其中的两个目标的发射角在脉冲数为319时重合,收发阵元数为M=N=4,SNR=10 dB,跟踪脉冲数为K=500,遗忘因子λ=0.85,AAJDd算法跟踪结果如图4所示,改进AAJDd算法跟踪结果如图5所示。

图4 PASTd算法目标跟踪结果Fig.4 Target tracking results based on PASTd algorithm
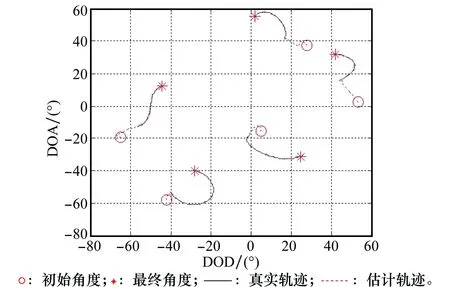
图5 改进PASTd算法目标跟踪结果Fig.5 Target tracking results based on improved PASTd algorithm
图4给出了PASTd算法跟踪运动目标的结果。PASTd算法估计的最后角度与目标角度重合,说明算法成功跟踪了目标。估计轨迹与真实轨迹基本重合,但是在K=319附近算法失效,这是因为脉冲数为319时,两个目标的发射角相同。图5中改进PASTd算法跟踪轨迹与真实轨迹完全重合,说明改进PASTd算法解决了PASTd算法不能跟踪相同发射角或接收角的目标的问题,并且PASTd算法初始角度到真实目标初始角度之间的连线为直线,能够更快的跟踪目标。
为了更好地比较PASTd算法与改进PASTd算法性能,给出跟踪误差定义:
仿真实验的条件与上一实验相同,仿真结果如图6所示。
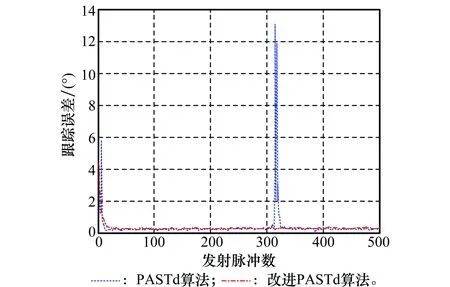
图6 两种算法的跟踪性能比较Fig.6 Comparison of tracking performance of two algorithms
从图6可以得出结论:PASTd算法和改进PASTd算法在K>50时跟踪误差较小,能够成功的跟踪目标,跟踪误差性能较好,说明两种算法在K>50都成功跟踪到了目标,算法收敛性较好。在脉冲数为319时,目标角度相同时,PASTd算法跟踪误差较大,算法失效,而改进PASTd算法仍能够成功的跟踪目标,验证了理论的正确性。
为了进一步说明本文算法的性能,设5个目标的运动模型不变,但是脉冲数分别设为200和400,即相当于目标运动速度发生改变,其余条件与上个实验相同,仿真结果分别如图7和图8所示。
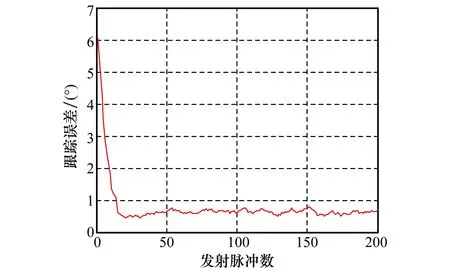
图7 脉冲数为200时本文算法跟踪结果Fig.7 Algorithm tracing result with the number of pulses is 200

图8 脉冲数为400时本文算法跟踪结果Fig.8 Algorithm tracing result with the number of pulses is 400
从图7和图8可以看出,脉冲为200和400时本文算法都能够成功跟踪目标,但是算法的性能和稳健性都随着脉冲数的减小而变差。这是因为随着脉冲数的降低,相当于目标运动速度变大,相邻两个时刻角度差变大,而本文算法假设相邻时刻目标角度变化较小,因此跟踪性能随着脉冲数的降低而变差,与理论分析一致。
实验2两种跟踪算法RMSE随SNR的变化关系
为了充分说明本文算法性能,将本文算法与PASTd算法的RMSE进行比较。假设空中存在角度相同的运动目标。设遗忘因子λ=0.85,收发阵元数都为5,发射脉冲数仍设为500,SNR=-5~20 dB。非稳定跟踪下的性能比较是没有意义的,因此选取100≤K≤500用于计算算法性能。仿真结果如图9所示。
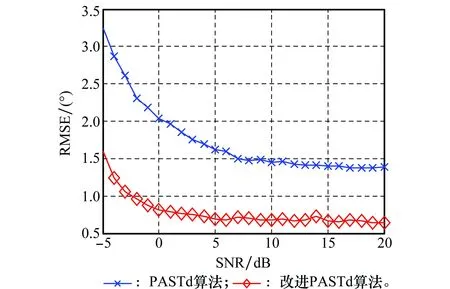
图9 RMSE随SNR的变化Fig.9 The change of RMSE along with SNR
从图9可以看出,改进PASTd算法RMSE低于PASTd算法,而且PASTd算法跟踪误差较大,说明改进PASTd算法已经失效,而改进PASTd算法能够成功跟踪相同角度的目标。改进PASTd算法与PASTd算法的RMSE差随着信噪比的降低逐渐增大,这是因为信噪比较低时,由于噪声的影响,PASTd算法中估计的特征矢量误差更大。
4 结 论
基于PASTd的双基地MIMO雷达目标跟踪算法不能跟踪相同角度的目标,并且无法完成目标收发角度配对及相关运算,影响算法的实用性。本文针对PASTd算法存在的问题,提出改进PASTd算法。改进PASTd算法在PASTd算法的基础上增加了目标角度自动关联配对算法,在此基础上利用得到的目标收发角度,求出的收发导向矢量,更接近真实的信号方向矢量,并且用其代替改进PASTd算法步骤一求出的特征矢量,用于下一时刻跟踪算法的初始矢量。本文算法解决了PASTd算法的问题,同时实现目标角度自动配对与关联运算,并且本文算法具有一般性,适用于所有基于PASTd算法的一大类跟踪算法。
[1] 陈浩文,黎湘,庄钊文.一种新兴的雷达体制——MIMO雷达[J].电子学报,2012,40(6),1190-1198.
CHEN H W, LI X, ZHUANG Z W. A rising radar system—MIMO radar[J].Acta Electronica Sinica,2012,40(6):1190-1198.
[2] FISHER E, HAIMOVICH A, BLUM R S, et al. Spatial diversity in radar-models and detection performance[J]. IEEE Trans.on Signal Processing, 2006, 54(3):823-838.
[3] ZHENG Z D, ZHANG J Y. Fast method for multi-target localization in bistatic MIMO radar[J]. IEEE Lectronics Letters, 2011, 47(2):138-139.
[4] ZHENG G M, TANG J, YANG X. ESPRIT and unitary ESPRIT algorithms for coexistence of circular and noncircular signals in bistatic MIMO radar[J].IEEE Access,2016,4:7232-7240.
[5] ZHANG Y, ZHANG G, WANG X H. Computationally efficient DOA estimation for monostatic MIMO radar based on covariance matrix reconstruction[J].Electronics Letters,2017,53(2):111-113.
[6] 张秦,张林让,郑桂妹,等.任意阵列双基地MIMO雷达的半实值MUSIC目标DOD和DOA联合估计[J].系统工程与电子技术,2016,38(3):532-538.
ZHANG Q, ZHANG L R, ZHENG G M, et al. Joint DOD and DOA estimation for bistatic MIMO radar with arbitrary array using semi-real-valued MUSIC[J]. Systems Engineering and Electronics, 2016, 38(3):532-538.
[7] TAN J, NIE Z P, WEN D B. Low complexity MUSIC-based direction-of-arrival for monostatic MIMO radar[J]. Electronics Letters, 2017, 53(4):275-277.
[8] ZAHERNIA A, DEHAHANI M J, JAVIDAN R. MUSIC algorithm for DOA estimation using MIMO arrays[C]∥Proc.of the Sixth International Conference on Telecommunication Systems, Services, and Application, 2011:149-153.
[9] 李建峰,张小飞.MIMO雷达嵌套平行阵下基于子空间的目标二维波达角估计[J].系统工程与电子技术,2017,39(3):522-528.
LI J F, ZHANG X F. Two dimensional direction of arrival estimation based on subspace for MIMO radar using nested parallel array[J]. Systems Engineering and Electronics,2017,39(3):522-528.
[10] ZHENG G M. DOA estimation in MIMO radar with non-perfectly orthogonal waveforms[J]. IEEE Communications Letters, 2017, 21(2):414-417.
[11] WANG X P, WANG L Y, LI X M, et al. An efficient sparse representation algorithm for DOA estimation in MIMO radar system[J]. IEEE Access 17th International Workshop on Signal Processing Advance in Wireless Communication, 2016:1-4.
[12] KHOMCHUK P, STAINVAS I, BILIK I. Pedestrian motion direction estimation estimation using simulated automation MIMO radar[J]. IEEE Trans.on Aerospace and Electronic Systems, 2016, 52(3):1132-1145.
[13] LI J F, JIANG D F, ZHANG X F. DOA estimation based on combined unitary ESPRIT for coprime MIMO radar[J]. IEEE Communications Letters, 2017, 21(1):96-99.
[14] YU H X, ZHANG X F, CHEN X Q, et al. Computationally efficient DOA tracking algorithm in monostatic MIMO radar with automatic association[J]. International Journal of Antennas and Propagation, 2014(12): 1-10.
[15] ZHANG X F, LI J F, FENG G P, et al. Kalman-PASTd based DOA tracking algorithm for monostatic MIMO radar[C]∥Proc.of the International Conference on Information, Services and Management Engineering, Beijing, 2011: 220-224.
[16] 李丽,邱天爽.双基地MIMO雷达目标参数估计及跟踪新算法[J].信号处理,2014,30(2):155-162.
LI L, QIU T S. A novel algorithm for target parameter estimation and dynamic tracking in bistatic MIMO radar system[J]. Signal Processing, 2014, 30(2):155-162.
[17] 张正言, 李小波, 徐旭宇, 等. 双基地MIMO雷达角度快速跟踪算法[J].信号处理, 2016,32(6):701-706.
ZHANG Z Y, LI X B, XU X Y, et al. Target angle rapid algorithm for bistatic MIMO radar[J]. Signal Processing,2016,32(6):701-706.
[18] ZHANG W T, LOU S T, LI X J, et al. Tracking multiple target in MIMO radar Via adaptive asymmetric joint diagonalization[J]. IEEE Trans.on Signal Processing, 2016, 64(11): 2880-2893.
[19] WU H L, ZHANG X F. DOD and DOA tracking for bistatic MIMO radar using PASTd without additional angles pairing[C]∥Proc.of the 5th IEEE International Conference on Advanced Computational Intelligence, 2012, 1132-1136.
[20] YANG B. Projection approximation subspace tracking[J]. IEEE Trans.on Signal Processing, 1995, 43(1): 95-107.

