基于高拉伸度遗传算法的相关干涉仪测向算法

王占刚, 王大鸣, 巴 斌, 张彦奎

(信息工程大学信息系统工程学院, 河南 郑州 450001)

0 引 言

信号到达角(direction of arrival, DOA)估计在目标定位、目标跟踪等领域中发挥着重要的作用[1-3]。而干涉仪测向体制结构简单,测向精度高,被广泛应用于到DOA估计[4-17]。但这种测向方法存在一个严重的问题,即当天线间基线长大于半波长时,测量相位差值分布在(-π,π),可能与理论值产生2π整数倍的相位模糊,导致测向结果失效。所以近年来国内外研究机构先后开展了解模糊算法的研究,力求解决干涉仪测向技术面临的这一难题。

解模糊算法一般分为基于线性天线阵[4]和基于立体天线阵[7]的测向算法,其中基于立体天线阵的解模糊算法具有天线阵排布灵活、精度较高的特点,但存在复杂度高的问题。文献[8]从解模糊入手,给出一种立体天线阵相关干涉仪测向方法,该方法能较好解决模糊问题,且适用于二维阵,测向精度较高,成为干涉仪测向研究的热点。然而,在利用这种方法进行结果搜寻时,方位角与俯仰角的取值范围内会存在多个局部最优值,因此,针对相关干涉仪测向算法的研究中,相位差模糊导致的强非线性问题成为研究的重点。

强非线性问题解决方法分为4大类,主要包括遍历法、随机搜索法、逐步渐进法、聚类法。遍历法的典型方法之一是网格法[9],该类方法搜索结果虽然比较可靠,但其复杂度较高,不利于结果快速收敛;随机搜索法的典型方法包括粒子群优化(particle swarm optimization, PSO)算法[10]、遗传算法(genetic algorithm, GA)[13]等,该类方法虽然具有一定的全局寻优能力,但搜索结果具有一定的随机性,且对初值的选取要求较高,对于这种极值较多的情况,需要进行较多代数的搜寻才能得到测向的最优值;逐步渐进法主要包括非线性最小二乘[14]、最速下降[15-16]等,这类算法在解决单峰问题时可以得到理想的结果,但在解决多峰问题时极易收敛到局部极值上,导致测向失效;聚类法包括基于径向基神经网络的相关干涉仪测向方法[17],该算法降低了算法复杂度,但是计算量为网格法的三分之一,仍比较大。综上所述,现有的寻优算法在搜索全局最大值时均存在一定的不足,因此,需要开展进一步研究,寻求适应性强、精度高且复杂度低的最大值搜索算法。

本文针对相位差模糊导致的强非线性问题,提出一种基于相关干涉仪模糊相位差的高拉伸度GA算法。该算法采用适应度处理机制,定义拉伸度的概念,通过改变目标位置附近适应度函数的拉伸度,增大全局最大值与其他值的差异,使选择结果更偏向于最大值,优化下一代。最后经过交叉、变异等过程得到精确的测向结果。

1 数学模型

相关干涉仪测向示意图在空间直角坐标系中,O为圆心处的观测天线,m表示以R为半径的圆上的观测天线,信号从俯仰角为θ,方位角为φ的方向射入,发射信号的波长为λ,如图1所示。

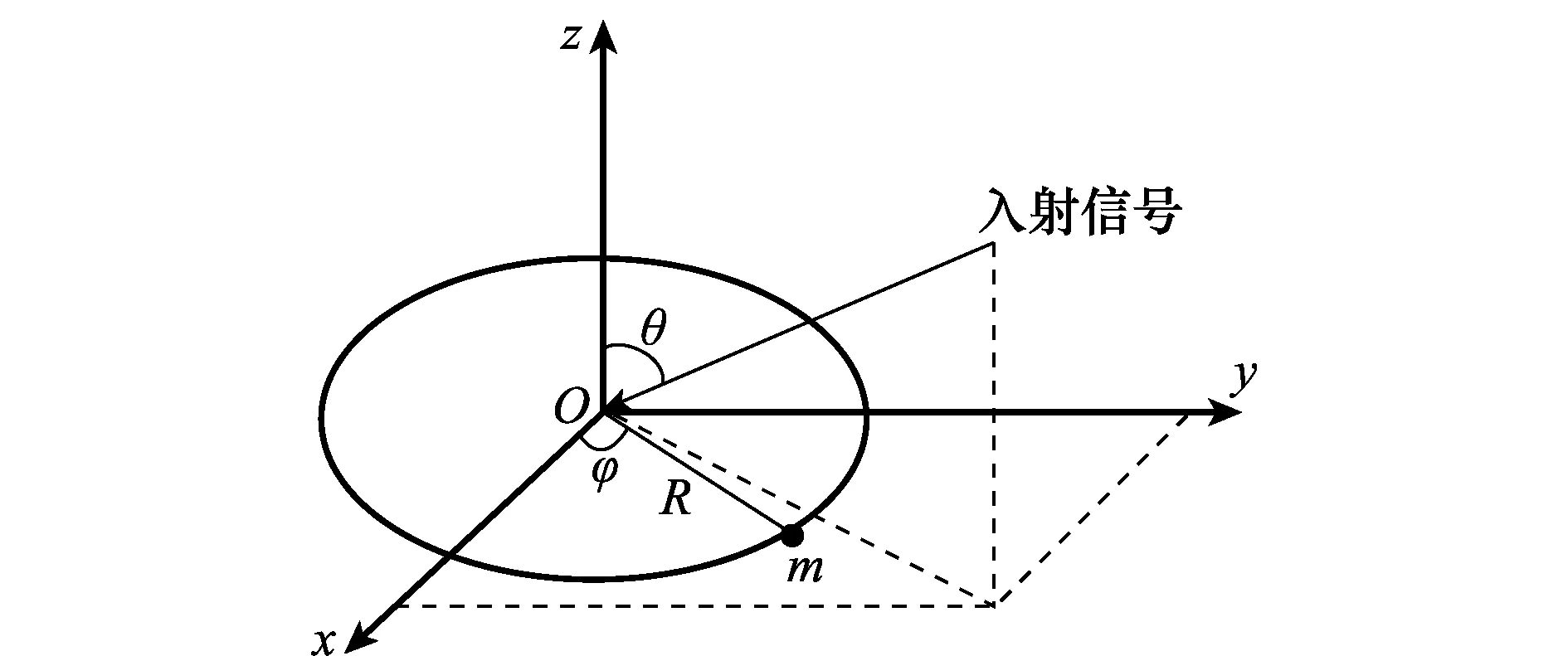
图1 相关干涉仪测向示意图Fig.1 Schematic diagram of correlative interferometer

根据圆阵列的几何性质,可得圆心处观测天线与圆上的天线之间相位差的理论值表达式如式(1)所示,以此建立方位角、俯仰角关于相位差的指纹库。

(1)

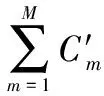
(2)

由于测量相位差的周期模糊效应,相关处理后多次测量得到的相关值C′(θ,φ)具有多峰特性,如何从众多局部最优值中选出全局最大值,是影响测向精度及复杂度的关键。

2 高拉伸度GA算法

通过对GA算法的原理分析可知,该算法本质上是根据个体适应度的不同,选择优秀的个体进入下一代,经过交叉、变异逐步得到最优解。所以本文从择优机制的设计入手,提出一种具有广泛适用性的高拉伸度遗传算法(genetic algorithm with high degree of stretching, HDS-GA)定义拉伸度的概念,通过提高在目标位置附近点的拉伸度,拉开全局最大值与局部最大值的差距,提高全局最大值周边节点的被选概率,从而实现子代优化,使算法能尽快收敛到全局最大值。

2.1 适应度函数设计

在本文研究中,将相关函数的相关值作为GA算法的适应度指标,从而将GA算法的适应度调整转化为对相关函数的相关值调整。主要包括模糊数处理与相关值处理两部分。

2.1.1 模糊数处理

为了表达出测量相位差与理论相位差之间的差值关系,消除测量值与理论值之间存在的2π相位差模糊的影响,用余弦函数来建立相关函数,即

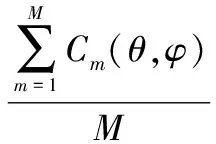
(3)

图2 相关干涉仪测向相关函数变化趋势Fig.2 Trend of related function in correlative interferometer

观察图2,此时相关函数存在多个峰值,起伏较大,直接搜索结果容易收敛到局部最优值。

2.1.2 适应度处理

为更好地描述本文算法,在以相关值作为适应度的基础上给出拉伸度的定义。

拉伸度:函数对其自变量的偏导数大小。函数在某一位置附近的拉伸度越大,表明与其他位置适应度的差距越大。

本文所提算法首先设计方便处理的适应度函数,然后求其偏导,根据在目标方向时适应度函数与其偏导趋于0的性质,设计新的适应度函数,使其在目标方向附近时拉伸度增大,从而扩大在目标方向与其他方向时适应度的差距,使结果更容易收敛。具体步骤如下:

步骤1适应度函数初步处理。为了方便得到角度估计结果,使全局最大值最接近于0,将适应度函数值都变为负数,整体减1,得到初步的适应度函数为

(4)

此时C0(θ,φ)的取值范围为(-2,0),含有多个峰值,且目标位置点为最大值点,适应度值接近于0。

步骤2初级适应度函数在目标方向附近时拉伸度求取。用初步得到的适应度函数对俯仰角求偏导,得

(5)

(6)

步骤3高拉伸度适应度函数求取。根据多重函数求偏导的性质,若想得到需要的目标适应度函数的偏导函数,可以通过将现有的适应度函数与其偏导函数的组合来实现。

(7)

C(θ,φ)=ln[-C0(θ,φ)]

(8)

适应度函数的变化趋势如图3所示。

图3 自然函数适应度函数变化趋势Fig.3 Trend of related function after preliminary

观察图3,虽然此时全局最大值附近拉伸度较大,全局最大值与其他局部最优值有所区分,但是区分程度并不明显。为了增大最大值与其他值的区分程度,增大分母中0的阶数,使目标位置附近的拉伸度更加接近于∞。将适应度函数的导数变为

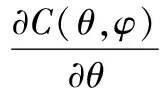
(9)

则适应度函数为

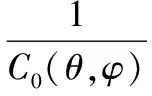
(10)

图4为最终适应度函数变化趋势。

图4 最终适应度函数变化趋势Fig.4 Trend of final related function

由图4可以很清晰地看出,目标方向附近拉伸度较大,全局最大值与局部最优值区分明显,达到了算法要求的目标。

在这里适应度函数的偏导中分母取初等函数C0(θ,φ)的平方时,基本可以达到本文的要求。若在其他情况下,处理结果仍不理想,可以通过增大分母中初等函数C0(θ,φ)的幂来调整适应度函数。需要特别注意,在进行上述分析时,用的是初等适应度函数在目标位置点接近于0的自身的性质,是一种不需要先验信息分析的优良算法。

2.2 高拉伸度遗传算法步骤

综上所述,本文所提的高拉伸度遗传算法流程如下:

步骤1随机产生数量为n的初始种群;

步骤3根据在目标位置处初等函数本身与其偏导数的性质,设计新的在目标位置附近偏导数趋近于无穷的适应度函数,增大目标位置处适应度函数的拉伸度。本文中推导出的高拉伸度适应度函数为

步骤4运用轮盘赌的方法选择下一代;

步骤5按照一定交叉概率进行单点交叉,随机选取一个点,以其为交叉位进行交叉,产生新的个体;

步骤6按照一定变异概率进行变异,随机产生一个变异位,产生变异的新个体;

步骤7由交叉和变异产生新一代种群,若此时达到了最大遗传代数或者本代种群最优值与前5代种群最优值坐标差小于10-3,输出结果;否则返回到步骤3。

3 仿真实验

本节假设在平地上用十元天线阵进行仿真,仿真场景:入射方位角与俯仰角均为20°,目标信号频率1.62 GHz,圆阵半径0.5 m,俯仰角的取值范围为0～90°,方位角的取值范围为0～360°。

3.1 性能分析

3.1.1 测向结果对比

遗传算法中取种群基数为500,遗传代数为50代,遗传精度为0.001,交叉概率为0.9,变异概率为0.1,分别用GA算法、高拉伸度GA算法做100次蒙特卡罗实验,对比测向结果,结果如表1所示。

表1 测向结果对比

由仿真结果可以看出,应用遗传算法寻优时,大部分结果都收敛到了局部最优值,这是因为局部最优值的适应度大小与全局最优值的适应度大小相差不大,在每一代中选择的下一代个体不能聚集于最优值所在峰上,在有限的遗传代数内导致结果收敛到局部最优值。而运用高拉伸度GA算法进行搜索,由于主峰适应度远远高于其他峰值,所以在选择时本文算法能很好地收敛到全局最优值,实现精确测向。

3.1.2 本文算法中种群基数对测向结果的影响

本文假设的条件下,遗传代数为30代,目标位置点随机生成,将种群基数分别取100、200、300、400、500的时候进行100次蒙特卡罗实验,计算测向误差,得到结果如图5所示。

图5 无模糊测向次数随种群基数的变化Fig.5 Unambiguous finding times with the change of thecardinality of population

由图5可以看出,本文算法实现无模糊测向次数随种群基数的增加而增加,这是因为当种群基数大时,随机取的初始点有的位于主峰内,不需要变异即可到达主峰;而种群基数小时,随机取的初始点不容易撒到主峰内,需要经过大量交叉变异才能到达主峰进而实现测向,但遗传代数有限,导致结果早熟,测向失效。且当为500时，基本可以保证实现准确测向,所以本文选定种群基数为500。

3.1.3 算法精度仿真

由于相关干涉仪测向算法不同于波束成形类算法与子空间类算法,其原理是利用鉴相器直接测量两天线间的相位差,然后遍历所有的俯仰角与方位角区间,根据距离关系得到理论相位差的指纹库,最后对比鉴相器得到的相位差与理论相位差之间的差距,最相近的相位差对应的俯仰角与方位角为角度估计结果。所以相关干涉仪测向方法在进行仿真加噪声时，都会直接加到相位差上。在角度均方误差为5°～25°的相位测量误差条件下,分别进行100次蒙特卡罗实验,评估算法测向精度。仿真中PSO算法种群基数取2 000个,代数取30代;网格法网格间距为0.1°;本文算法种群基数取500个,遗传代数取40代,得到测向误差结果如图6所示。

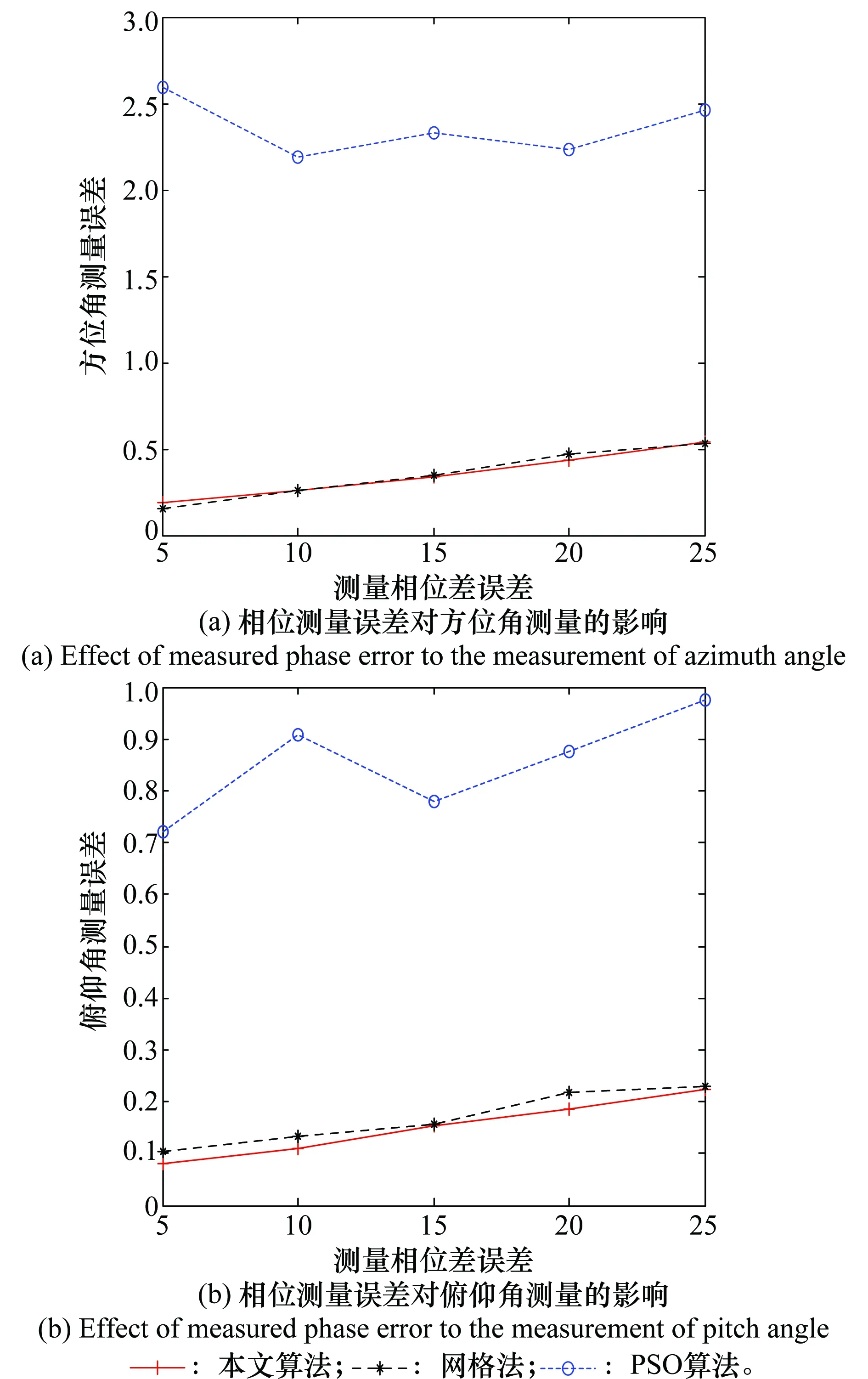
图6 相位测量误差对测向精度的影响Fig.6 Effect of measured phase error to direction finding accuracy

由图6可以看出,本文所提出的HDS-GA算法测向精度远远优于可以实现全局寻优的PSO算法,且接近于精度较高的网格法,这是因为PSO算法通过随机地跳变寻找全局最优值,在最大值附近时跳动幅度过大,导致精度相对较低;网格法通过遍历比较每一个相关函数值来寻找全局最大值,所以精度高;本文所提HDS-GA算法通过变换相关函数降低其他局部最大值的适应度,增加了主峰内的值被选择的概率,优化下一代,通过交叉变异逐步收敛到最大值,测向精度略优于网格法,具有良好的全局寻优性能。

3.2 复杂度分析

本节对本文算法、网格法、PSO算法分别作100次仿真实验进行性能对比,结果如表2所示。

表2 不同方法性能对比

对于网格法、PSO算法、本文算法来说,复杂度主要体现在适应度的计算上,通过仿真时间表明，算法中的对比、交叉、变异、飞跃等操作相对于大量的适应度计算来说占很小的比重,所以只考虑适应度的运算量。对于网格法,普通相关干涉仪测向网格划分的宽度为0.1°,相关处理次数为3 600×900次,需要3 600×900×10次余弦运算以及大量对比运算,最后比较全部数值得到最优值,计算复杂度极高,平均计算一次需要629.60s,但测向精度较高;本文中提出的高拉伸度GA算法在本文参数条件下最多计算500×40次适应度,共500×40×10次余弦运算以及500×40次除法运算,复杂度降低,且得到结果的精度较高,平均误差为0.34°。最后又用可以进行全局搜索的PSO算法进行了对比仿真,这种算法具有良好的全局寻优能力,在本文参数条件下最多共计算2 000×30次适应度,共2 000×30×10次余弦运算,复杂度适中,但其精度不高,平均误差为2.26°,且有4次测向失效。

4 结 论

本文针对相关干涉仪测向方法中存在的全局最大值搜索问题,给出了一种基于高拉伸度的改进GA算法。该算法根据GA算法的选择机制,优化适应度函数,利用适应度函数及其偏导数在目标位置点附近趋近于0,而在其他位置点适应度函数的值离0较远的特性,提升了主峰附近点的拉伸度,增大全局最大值点与其他点的差距,提高主峰个体被选择的概率,加快算法的收敛速度。最后通过仿真表明,相对于网格法和PSO算法,本文所提出的算法不需要遍历全部目标区域,可以逐步逼近最大值,在保证精度的同时降低了运算量,且算法稳定,测向精度高。所提算法高拉伸度的思想也可以应用于其他求解最大值的问题中,具有广泛的适应性。

[1] YANG R, FOO P H, NG B P, et al. RF emitter geolocation using amplitude comparison with auto-calibrated relative antenna gains[J]. IEEE Trans. on Aerospace & Electronic Systems, 2011, 47(3): 2098-2110.

[2] MACPHIE R H, YOON T H. On Using the compound interfe-rometer to obtain the power pattern of a conventional receiving array[J].IEEE Trans.on Antennas & Propagation，2009,57(10):3356-3359.

[3] 张敏,郭福成,周一宇,等.时变长基线2维干涉仪测向方法[J].电子与信息学报,2013,35(12):2882-2888.

ZHANG M, GUO F C, ZHOU Y Y, et al. Direction finding method for two-dimension interferometer using the time varying long baseline[J]. Journal of Electronics&Information Technology, 2013,35(12): 2882-2888.

[4] 毛虎, 杨建波, 刘鹏,等. 干涉仪测向技术现状与发展研究[J]. 电子信息对抗技术, 2010, 25(6):1-6.

MAO H, YANG J B, LIU P, et al. The actuality and development of phase interferometer technology[J]. Electronic Information Warfare Technology, 2010, 25(6): 1-6.

[5] 曲志昱,司锡才.基于虚拟基线的宽带被动导引头测向方法[J].弹箭与制导学报,2007,27(4): 92-95.

QU Z Y , SI X C . Direction finding method of wideband passive radar seeker based on virtual baseline[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2007, 27(4): 92-95.

[6] 韩永泉. 余数定理解干涉仪模糊初步研究[J]. 电子信息对抗技术, 2008, 23(4): 46-47.

HAN Y Q. Preliminary study on defuzzification using remainder theorem[J]. Electronic Information Warfare Technology, 2008, 23(4): 46-47.

[7] 张春杰, 李智东. 非均匀圆阵天线模型解模糊误差研究[J]. 系统工程与电子技术, 2012, 34(8): 1525-1529.

ZHANG C J, LI Z D. Research on solving ambiguity error of nonuniform circular antenna array model[J]. Systems Engineering and Electronics, 2012, 34(8): 1525-1529.

[8] 李淳, 廖桂生, 李艳斌. 改进的相关干涉仪测向处理方法[J]. 西安电子科技大学学报:自然科学版, 2006, 33(3): 400-403.

LI C, LIAO G S, LI Y B. A DF method for the improved corre-lative interferometer[J].Journal of Xidian University,2006,33(3):400-403.

[9] CHEN Y, CHENG L, LI M, et al. Multiscale grid method for detection and reconstruction of building roofs from airborne LiDAR data[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2014, 7(10): 4081-4094.

[10] CHEN S M, CHIOU C H. A new method for multiattribute decision making based on interval-valued intuitionistic fuzzy sets, PSO techniques and evidential reasoning methodology[J]. IEEE Trans. on Fuzzy Systems, 2015, 1(6): 403-409.

[11] SCOTT-HAYWARD S, GARCIA-PALACIOS E. Channel time allocation PSO for gigabit multimedia wireless networks[J]. IEEE Trans. on Multimedia, 2014, 16(3): 828-836.

[12] ALIK B, TEGUAR M, MEKHALDI A. Minimization of ground-ing system cost using PSO, GAO, and HPSGAO techniques[J]. IEEE Trans. on Power Delivery, 2015, 30(6): 1-1.

[13] CHENG Y F, SHAO W, ZHANG S J, et al. An improved multi-objective genetic algorithm for large planar array thinning[J]. IEEE Trans. on Magnetics, 2016, 52(3): 1-4.

[14] ZHANG L, LI K, BAI E W, et al. Two-stage orthogonal least squares methods for neural network construction.[J]. IEEE Trans.on Neural Networks & Learning Systems,2014,26(8):1608-1621.

[15] WU Y M, JIANG L J, SHA W E I, et al. The numerical steepest descent path method for calculating physical optics integrals on Smooth conducting quadratic surfaces[J]. IEEE Trans.on Antennas & Propagation,2013,61(8):4183-4193.

[16] QIN X, YAN Z, HE G. A near-optimal detection scheme based on joint steepest descent and Jacobi method for uplink massive MIMO systems[J]. IEEE Communications Letters, 2015, 20(2): 276-279.

[17] 赵雷鸣. 基于RBF神经网络的相关干涉仪测向方法[J]. 无线电工程, 2011, 41(1):15-17.

ZHAO L M .The DF method of correlative interferometer based on RBF neural network[J]. Signal and Information Processing, 2011,41(1): 15-17.