外壁转速对圆环扇形截面流道内流动特性的影响
王宗勇, 王舒婷, 崔艳军, 陈科昊
(1.沈阳化工大学 能源与动力工程学院, 辽宁 沈阳 110142 2.中国石油天然气第八建设有限公司, 辽宁 抚顺 113006)
现有文献大多对矩形及扇形流道内的流场进行分析,而针对周向雷诺数对流体速度场及涡流分布的影响缺乏系统清晰的阐述.为此,本文基于前人研究结果运用数值模拟方法探究周向雷诺数对内壁固定外壁旋转的环扇形截面直流道内流体的三维速度分布及涡流区域变化规律的影响.
1 数值模拟
1.1 物理模型
建立一个圆环扇形截面流道,如图1所示.
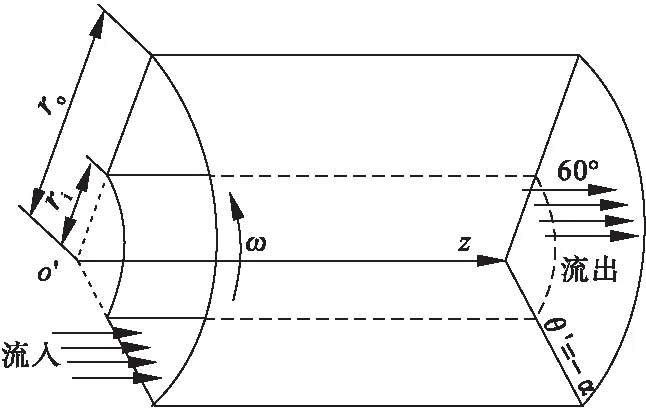
图1 圆环扇形流道横截面结构及其边界条件
该流道由2个同轴圆柱面及2个通过圆柱面轴线的平面构成,平面夹角2α=60°,外圆柱面半径ro=50 mm,内圆柱面半径ri=25 mm,外圆柱面以恒定角速度ω旋转,内圆柱面及其余2个平面固定不动,流体由入口面流入,由出口面流出.流体在轴向压力及外圆柱面旋转作用下在流道内螺旋流动,忽略流道长度对流动特性的影响,假定流体沿轴向充分发展.为便于分析,对该流道建立圆柱坐标系,以圆柱面轴线作为z轴,角度坐标起始位置o′位于圆环扇形截面的角平分线上.
1.2 网格划分及边界条件
在Fluent的前处理软件Gambit中对该圆环扇形流道进行网格划分,采用六面体网格,为确定最佳网格尺寸,以摩擦因子f=2dhΔp/(Lρu2)为指标,对不同网格间距进行网格无关性验证,其中Δp为压力降,ρ为流体密度,L为环扇形流道轴向长度,u为入口平均速度,水力直径dh=4S/C,S为环扇形截面面积,C为环扇形截面周长.通过网格无关性验证,确定面网格间距为0.6 mm.
采用周期性边界条件对充分发展的流体流动特性进行模拟.在模拟过程中取轴向雷诺数Rez=ρudh/μ=10保持不变,而外圆柱面旋转速度分别取多个值进行模拟,分析不同旋转速度下流动特性的变化规律.定义周向雷诺数Reθ=ρωro2/μ,表征流体周向流动状态,在Reθ=0.1~500范围内模拟15个周向雷诺数工况.
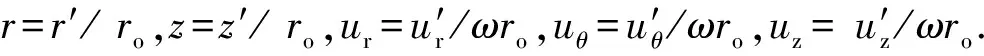
2 各速度分量分布
2.1 轴向速度
由于流体在流道内充分发展,各截面速度分布相同,因此任取某一截面的模拟结果进行分析,探究外圆柱面转速对环扇形截面流道内流体的速度分布影响,结果如图2所示.
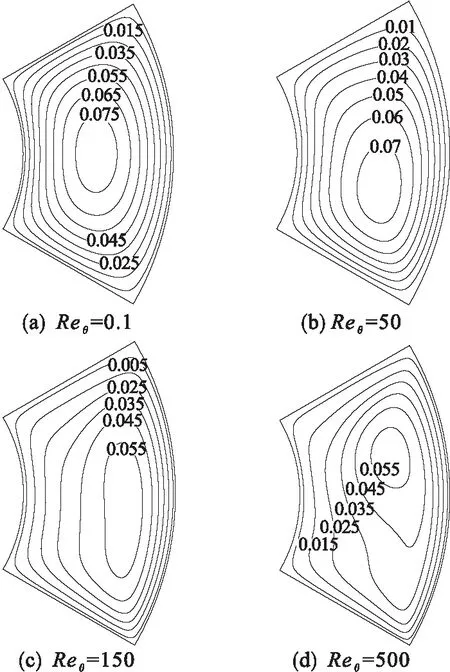
图2 轴向速度等值线
由图2(a)~(d)可以看出:在周向雷诺数很低的情况下,轴向速度以环扇形夹角平分线为对称轴呈对称分布状态,轴向速度中心(最大轴向速度位置)位于对称轴上,随着外圆柱面转速的增大,轴向速度中心逐渐发生偏移,起始其周向偏移方向与外圆柱面旋转方向相反即顺时针偏移,径向偏移方向为由内向外,轴向速度不再呈现对称状态;当外圆柱面转速继续提高到某一程度时,轴向速度中心开始出现反向偏移即向内逆时针偏移直至保持不动.
为进一步定量确定轴向速度中心位置与外圆柱面转速即周向雷诺数的关系,对不同周向雷诺数下的轴向流动特性进行数值计算,绘制轴向速度中心径向位置和周向位置与周向雷诺数的关系图,如图3所示.由图3(a)可以看出:当Reθ<110时,轴向速度中心与周向雷诺数成线性规律向外圆柱壁面靠近;当Reθ=110~150时,虽然中心位置依然向外圆柱面偏移,但变化幅度极小;在Reθ>150后,周向速度中心偏移方向发生变化,逐渐向内圆柱面偏移.由图3(b)可知:轴向速度中心先是顺时针偏转,当Reθ>90后轴向速度中心开始逆时针偏转;当Reθ>300后轴向速度中心的周向位置几乎保持不变.
层次分析法是解决多目标、多层次复杂问题的常用方法,通常总目标下设若干子目标,子目标又由多个层次构成,通过专家评分法模糊量化各级指标的排序,以此结果作为决策依据[20]。过程如下:
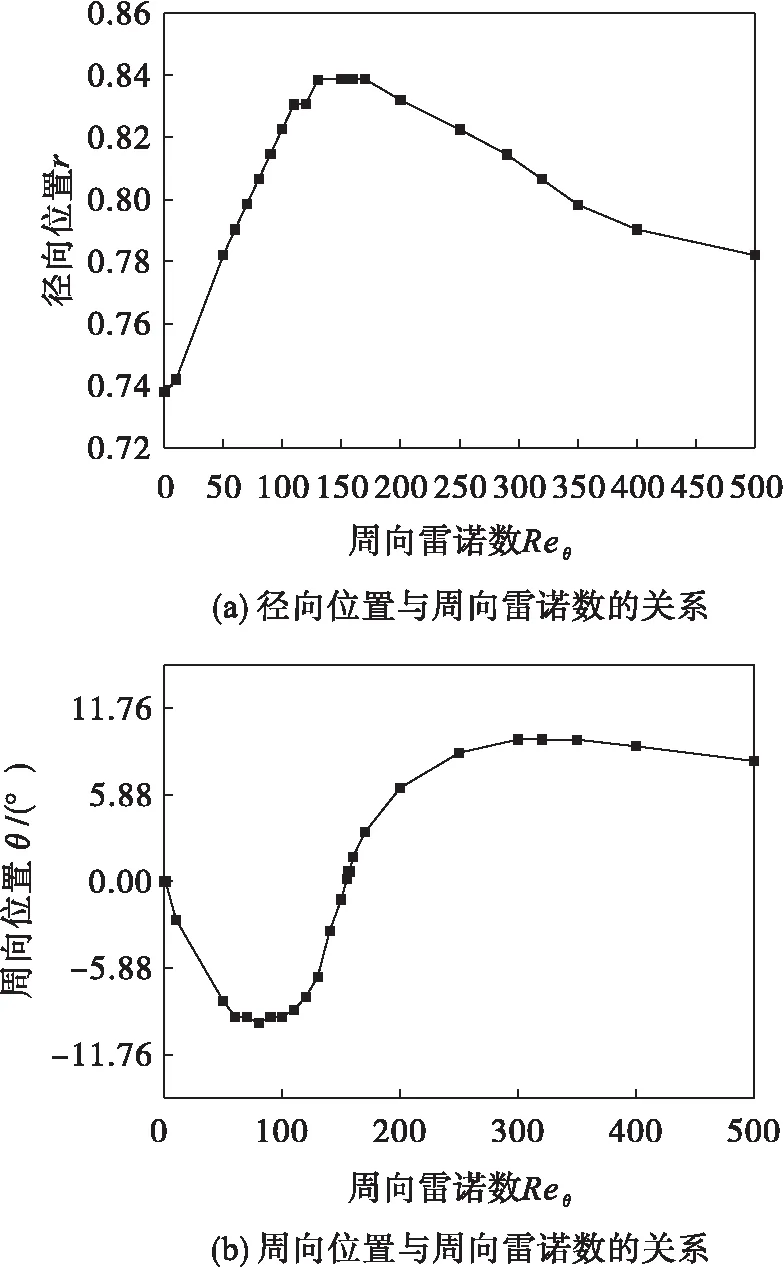
图3 周向雷诺数对轴向速度中心位置的影响
2.2 径向速度
流道内流体的径向流动对于流体的对流传热具有重要作用,掌握其分布规律有助于具有该类流动特性流道的换热器或反应器的工业化应用.
如图4(a)所示,当周向雷诺数很低时,径向速度关于中心线呈反对称分布,对称线两侧流体的径向流动方向相反,外圆柱面两侧角点处径向速度值最大.随着周向雷诺数不断增大,流动方向相反的径向速度分界线(零值线)发生扭曲并向逆时针方向偏移,径向速度等值线也相应产生形状变化.当Reθ=160时,下部的径向流动区域出现了另外一个径向速度中心,如图4(c)所示.随着周向雷诺数的进一步增大,靠近内圆柱面下角点处径向流动区域的面积开始明显增大,致使下半部的径向流动区域具有3个速度中心,这种流动现象说明随着外圆柱面旋转速度的增大,强化了流道内流体的径向流动,径向速增大、径向流动区域增多.

图4 径向速度等值线图
2.3 周向速度
流道内流体的周向运动是由外圆柱面对流体的黏滞作用在其旋转带动下产生的,外圆柱面的转速对于流道内流体的周向流动规律具有决定性的影响.由图5(a)可知:外圆柱面旋转速度较低时,周向速度与流道角平分线呈对称分布状态,速度等值线主要由两部分组成,一部分是靠近外圆柱面的与其旋转方向相同的正值区域,另一部分是靠近内圆柱面与外圆柱面旋转方向相反的负值区域,这两部分的分界线代表周向速度为零.由图5(b)可以看出:随着周向雷诺数的增加,正负周向流动区域分界线发生扭曲变形,上部向内下部向外偏转,同时顺时针周向流动(等值线值为负数)的速度中心沿逆时针方向产生偏移,并且等值线的形状随着雷诺数的增大越来越偏离流道外壁轮廓,见图5(c).当Reθ=500时,出现了多个较为明显的周向速度中心,代表流道内流动周向运动更为强烈,分布区域更为广泛.

图5 图5 周向速度等值线图
3 不同径向位置速度对比
为详细探究流道内的速度分布,选取不同周向雷诺数下将流道沿径向4等分了3条弧线(r=0.625、0.75、0.875)上的速度进行对比分析,将弧线上各点的轴向速度、径向速度和周向速度以外壁旋转线速度为基准进行无量纲化处理.如图6所示,各图中速度表示无量纲处理后的量.
由图6(a)可以看出:当周向雷诺数很低时周向速度和轴向速度与流道角平分线成对称分布关系,角平分处速度最大,而径向速度与流道角平分线成反对称关系,靠近两侧平板壁面处角速度最大,与前面速度等值线图分析结果一致,同时由该图还可知径向速度和周向速度属于同一个量级,而轴向速度与其相比要小一个量级.
由图6(b)可以看出:不同径向位置的速度分布曲线扭曲,速度分布的对称性明显下降,另外个别位置速度大小也发生明显改变,比如靠近外圆柱面的轴向速度增大,说明外圆柱面转速提高不仅增强了流体周向流动,同时也强化了近壁面的轴向流动.
由图6(c)可以看出:轴向速度中心周向位置产生反向偏移,说明周向雷诺数大于某一值后,外圆柱面诱导产生的惯性力占据主导地位,致使轴向速度中心偏心其转动方向一侧.而径向速度变化最为明显,由内向外运动的流体速度提高并出现在流道角平分线附近,说明当外圆柱面转速达到一定程度后,流道内流体径向流动强度得到明显强化,满足该条件可以强化流道内的对流传热或混合.此外由图6(c)可知流道中径圆弧上的周向速度随着外圆柱面转速的提高而相应降低,说明外圆柱面所输入的流体周向流动的驱动力和固定壁面所产生的摩擦力处于相对平衡状态,两者控制的流动区域范围大体相当.
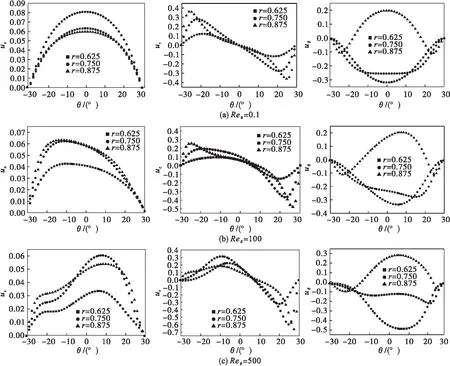
图6 不同径向位置速度对比
4 涡流特性
在上述速度分布的等值线图中可以看出当外圆柱面转速达到某一值后,径向速度和周向速度明显出现多个速度中心,在一定程度上代表可能具有多个涡流区域.但要确定流道内的涡流特性必须采用流线来分析流体质点的流动轨迹,为此本文绘制出了不同周向雷诺数下流道横截面内的流线等值线图,如图7所示.
由图7(a)可知:当周向雷诺数很小时,横截面内被一个主涡流区域几乎完全占据,仅在内圆柱面上下两个角点处存在两个极其微小的Moffatt涡,这两个Moffatt涡主要取决于流道截面形状,即与流道的扇形角度和内圆柱面半径密切相关.当周向雷诺数Reθ=150时,可以看出主涡流区域中心产生逆时针偏移,流线形状也发生一定改变,两个Moffatt涡也有所增大但不是十分明显.当周向雷诺数进一步增大后,主涡流区域中心位置变化微小,核心区的流线形状椭圆度降低,更加趋近于圆,此外更为重要的特征是两个Moffatt涡所占区域面积随着外圆柱面转速的提高显著增大,特别下角点处的Moffatt涡的面积增加幅度更为突出,Reθ=300与Reθ=150时左下角Moffatt涡面积相比增大8倍左右.当Reθ=500时,可以明显看到左下角Moffatt涡的流线为顺时针,而主螺旋涡为逆时针旋转,由此可以判断左上角的Moffatt涡应是顺时针旋转.
流道内的主螺旋涡是在外圆柱面旋转带动下形成的,外圆柱面的转速影响着主螺旋涡形态,在高转速下主螺旋涡中心偏向右上角,从而导致离其较远的左下角静压减小,左下角的Moffatt涡由于低压的牵引作用向外扩张,形成一个较大的顺时针旋转流动区域.流道内螺旋涡增多有助于流体的对流传热及近壁流体更新,可以将具有这种流动特性的流道应用到换热器或混合器之中.
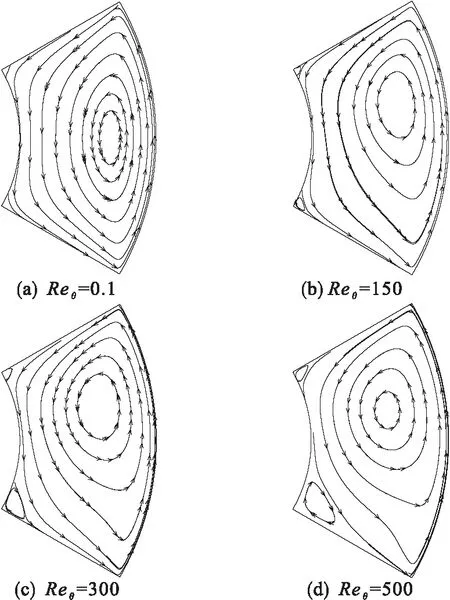
图7 横截面流线图
5 结 论
(1) 扇形流道内的流体在轴向压降及外圆柱壁面旋转作用下形成三维螺旋流,螺旋流速度分布规律与外壁转速密切相关.
(2) 在较低的外壁转速下,周向速度和轴向速度与扇形流道截面角平分线成对称关系,而径向速度与角平分线成反对称关系.随着外壁转速的提高三维速度分量的对称或反对称关系遭到破坏,速度中心的径向及周向位置随外壁转速产生有规律变化.
(3) 外壁旋转的圆环扇形流道内具有3个涡流区域,其中靠近外圆柱面的主螺旋涡旋转方向与外壁面旋向相同,而靠近内圆柱面上下角点的两个Moffatt涡旋向与外壁面转动方向相反.主螺旋涡在外圆柱面带动下向其旋转方向偏移,而距离主螺旋涡中心较远的Moffatt涡在低压作用下涡流区域随外壁转速的提高而显著增大.
[1] SAATDJIAN E,RODRIGO A J S,MOTA J P B.Stokes Flow Heat Transfer in an Annular,Rotating Heat Exchanger [J].Applied Thermal Engineering,2011,31(8):1499-1507.
[2] BOZEMAN J D,DALTON C.Numerical Study of Viscous Flow in a Cavity[J].Journal of Computational Physics,1973,12(3):348-363.
[3] GÜRCAN F,GASKELL P H,SAVAGE M D,et al.Eddy Genesis and Transformation of Stokes Flow in a Double-Lid Driven Cavity[J].Journal of Mechanical Engineering Science,2003,217(3):353-364.
[4] GALAKTIONOV O S,MELESHKO V V,PETERS G W M,et al.Stokes Flow in a Rectangular Cavity with a Cylinder[J].Fluid Dynamics Research,1999,24(2):81-102.
[5] KELMANSON M A,LONSDALE B.Eddy Genesis in the Double-Lid-Driven Cavity[J].The Quarterly Journal of Mechanics and Applied Mathematics,1996,49(4):635-655.
[6] 孟俊苗,邓子辰,王艳.矩形空腔内Stokes流的状态空间有限元法[J].计算力学学报,2014,31(2):205-211.
[7] 何士华,张立翔,胡吉敏,等.哈密顿体系下求解矩形域Stokes流的端部效应研究[J].昆明理工大学学报(自然科学版),2013,38(4):95-101.
[8] KHAKHAR D V,FRANJIONE J G,OTTINO J M.A Case Study of Chaotic Mixing in Deterministic Flows:The Partitioned-Pipe Mixer [J].Chemical Engineering Science,1987,42(12):2909-2926.
[9] KHAKHAR D V,MCCARTHY J J,OTTINO J M.Mixing and Segregation of Granular Materials in Chute Flows[J].Chaos,1999,9(3):594-610.
[10] 刘仁昇,程铎.静态混合器的设计和应用〈KENICS 螺旋型叶片〉[J].化学反应工程与工艺,1986,2(3):79-91.
[11] 张小艳,姜芳芳.螺旋管换热技术的研究现状综述[J].制冷与空调,2014,28(1):75-80.
[12] KHURI S A.Biorthogonal Series Solution of Stokes Flow Problems in Sectorial Segions[J].SIAM Journal on Applied Mathematics,1996,56(1):19-39.
[13] KRASNOPOLSKAYA T S,MELESHKO V V,PETERS G W M,et al.Mixing in Stokes Flow in an Annular Wedge Cavity[J].European Journal of Mechanics-B / Fluids,1999,18(5):793- 822.
[14] GÜRCAN F,BILGI H.Bifurcations and Eddy Genesis of Stokes Flow Within a Sectorial Cavity[J].European Journal of Mechanics-B/Fluids,2013,39:42-51.
[15] WANG Z Y,ZHAO J Y,WU J H.Stokes Flow Characteristics in a Cylindrical Quadrant Duct with Rotating Outer Wall[J].Journal of Fluids Engineering,2014,136 (11) :111-202.
[16] 王宗勇,赵家瑜,吴剑华,等.扇形流道内Stokes流动特性的数值模拟[J].沈阳化工大学学报,2015,29(1):37-42.
[17] 王宗勇,赵家瑜,吴剑华,等.扇形截面流道Stokes流速度场的解析解[J].机械工程学报,2014,50(18):193-202.
[18] 王艳,邓子辰.Stokes流问题的环向辛对偶求解方法[J].机械科学与技术,2008,27(3):374-378.
[19] 王艳,邓子辰.Hamilton体系下环扇形域的Stokes流动问题[J].计算力学学报,2008,25(2):144-149.
[20] 麻剑锋,沈新荣,章本照,等.旋转环形偏心圆截面弯管内流动特性分析[J].浙江大学学报,2005,39(11):1829-1832.

