类比思想解决立体几何问题

■郑州市第十一中学1 8 0 5班 曹雪源

类比思想解决立体几何问题

■郑州市第十一中学1 8 0 5班 曹雪源

类比思想是一种十分重要的数学思想,对于高考中出现的立体几何问题,利用类比可以给我们提供新的思路和方法。利用类比思想解决立体几何问题的思路:二维平面→三维立体;直线→平面;平面圆→空间球。遵循着这三条路线,可以发现新结论,解决新问题。

下面以平面中点到直线的距离公式类比空间点到平面的距离公式为例进行说明。

类比1：二维直线方程→三维空间平面方程。平面中直线l的普通方程为A x+B y+C=0,由此类比,空间中平面α的普通方程为A x+B y+C z+D=0。

类比2：平面中点到直线的距离公式→空间中点到平面的距离公式。平面中点P(x0,y0)到直线l:A x+B y+C=0的距离公式为d=,由此类比,空间中点P(x,0y0,z0)到平面α:A x+B y+C z+D=0的距离公式为(此处涉及高数内容,证明略)

例题 (2 0 1 7年文科数学卷改编)如图1,四棱锥PA B C D中,侧面P A D为等边三角形且垂直于底面A B C D,∠B A D=∠A B C=9 0°。

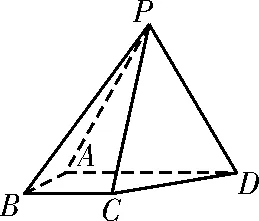
图1

(1)证明:直线B C∥平面P A D;

(2)求点B到平面P C D的距离。

解析：(1)因为∠B A D=∠A B C=9 0°,所以B C∥A D且A D⊂平面P A D,所以B C∥平面P A D。

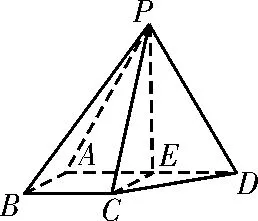
图2

(2)解法1:(常规解法)如图2,设A D的中点为E,连接P E,C E,所以四边形A B C E是边长为1的正方形,所以因为△P A D是正三角形,平面P A D⊥平面A B C D,E为A D的中点,所以P E⊥平面A B C D。所以中,由余弦定理得所以点B到平面P C D的距离d解法2:(利用类比公式求解)以A D的中点E为原点建立如图3所示的空间直角坐标系E-x y z。设平面P C D的方程为A0x+B0y+C0z+D0=0,将点P(0,0,3),C(1,0,0),D(0,1,0)的坐标代入得令D0=-3,得A0=B0=3,C0=1,故平面P C D的方程为3x+3y+z-3=0。所以点B(1,-1,0)到平面P C D的距离为d=

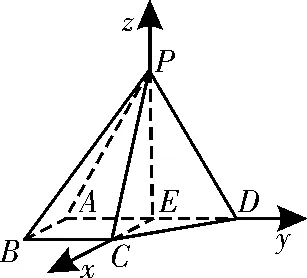
图3

可以看到,立体几何问题在引入空间直角坐标系后,在类比思想的帮助下,点到平面的距离问题迎刃而解。

(责任编辑 刘钟华)