数学试题中的数学文化与赏析

■河南省南阳市第一中学 王红武

数学试题中的数学文化与赏析

■河南省南阳市第一中学 王红武

近年来,数学试题中关于数学文化方面的考题屡见不鲜。大多是从中国古代数学著作中选取材料片段,结合当前高中数学教学背景,体现了中华古代文明与现代文明的交相辉映。重在考查考生的阅读能力和数学学科素养,强调数学知识体系与实际应用。本文选取部分数学文化题目,供读者参考。

一、以数学史为背景的数学文化题

例1 正方形A B C D内的图形来自中国古代的太极图,如图1。正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称。在正方形内随机取一点,则此点取自黑色部分的概率是( )。

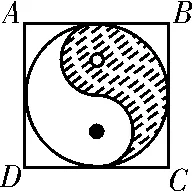
图1

解析：设正方形边长为2,则圆的半径为1,正方形的面积为2×2=4,圆的面积为π×12=π,图中黑色部分的面积为,则此点取自黑色部分的概率为故选B。

例2 图2所示的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为1 4,1 8,则输出的a为( )。

A.0 B.2 C.4 D.1 4

解析：由题意知输出的a是1 8,1 4的最大公约数为2,选B。

评注:此题源于《九章算术》卷第一《方田》之[六]:“又有九十一分之四十九。问约之得几何。可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也。以等数约之”。后人称之为“更相减损术”,它是求最大公约数的伟大创举。

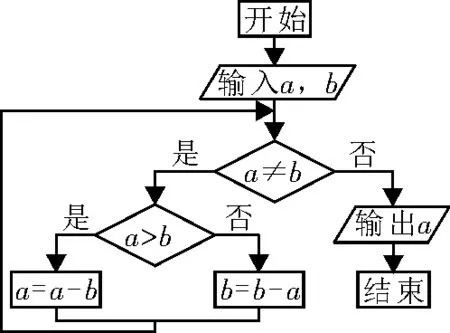
图2

二、以数学应用为背景的数学文化题

例3 小敏打开计算机时,忘记了开机密码的前两位,只记得第一位是M,I,N中的一个字母,第二位是1,2,3,4,5中的一个数字,则小敏输入一次密码能够成功开机的概率是( )。

解析：开机的密码可能有(M,1),(M,2),(M,3),(M,4),(M,5),(I,1),(I,2),(I,3),(I,4),(I,5),(N,1),(N,2),(N,3),(N,4),(N,5),共1 5种,则小敏输入一次密码能够成功开机的概率是,故选C。

评注:本题以生活实际为背景,考查对古典概型的理解应用。

例4 甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩,老师说,你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩,看后甲对大家说:我还是不知道我的成绩。根据以上信息,则( )。

A.乙可以知道两人的成绩

B.丁可能知道两人的成绩

C.乙、丁可以知道对方的成绩

D.乙、丁可以知道自己的成绩

解析：由甲的说法可知乙、丙一人优秀一人良好,则甲、丁一人优秀一人良好,乙看到丙的结果则知道自己的结果,丁看到甲的结果则知道自己的结果,故选D。

评注:本题以生活实际为背景,考查数据处理能力和数理逻辑推理能力。从众多数据中,挑选关键数据进行分类讨论,一般利用反证法、类比法、分析法得到结论。

数学的历史告诉我们数学从哪里来,将要去哪里,数学的发展历史中贯穿着一种探索精神和治学之道,在数学学习中适时、适当地引入数学文化知识,可以帮助同学们合理构建知识体系,培养同学们的数学素养。

(责任编辑 刘钟华)