概率统计知识结构与拓展

■河南省南阳市第一中学 王喜朝

概率统计知识结构与拓展

■河南省南阳市第一中学 王喜朝

编者的话：基本知识和基本技能是高中数学的核心,同学们一定要高度重视。本期特约河南省南阳市第一中学王喜朝等几位老师为同学们解读相关知识。河南省南阳市第一中学是河南省名牌高中,多年来高考成绩一直在全省名列前茅。愿同学们通过阅读,能从中感悟知识的结构与拓展,把握高考命题特点与趋势。

一、知识结构框架

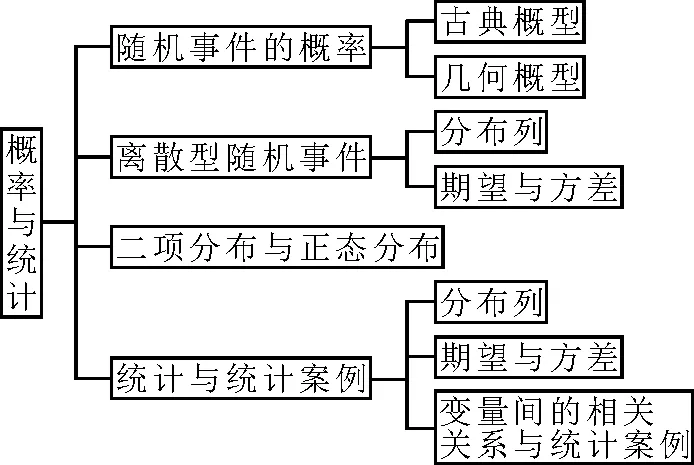
二、结构分析

在大量的不确定数据中隐藏着确定性的规律,这便是概率统计的核心内容,人们发现并利用这些规律为生产实践活动服务则是概率统计的核心价值,概率统计从诞生之日起便带有很强的应用性。统计数据需要进行随机抽样,进而计算这些数据的数字特征,并根据茎叶图与频率分布直方图用样本去估计总体。数据显示,有些变量之间存在着相关关系,人们用列联表计算变量的相关程度,用最小二乘法找到了具有线性相关关系的两个变量的回归直线方程。人们还发现了一些有用的概率模型,掌握了一些随机变量的分布列及数字特征。

三、实例分析

1.计数背景下的概率。

例1 某市公租房的房源位于A,B,C三个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,求该市的任意4位申请人中:

(Ⅰ)恰有2人申请A片区房源的概率;

(Ⅱ)申请的房源所在片区的个数ξ的分布列与期望。

分析：这是等可能性事件的概率计算问题,属古典概型。

解：(Ⅰ)所有可能的申请方式有34种,恰有2人申请A片区房源的申请方式有种,所以恰有2人申请A片区房源的概率为

(Ⅱ)ξ的所有可能值为1,2,3。

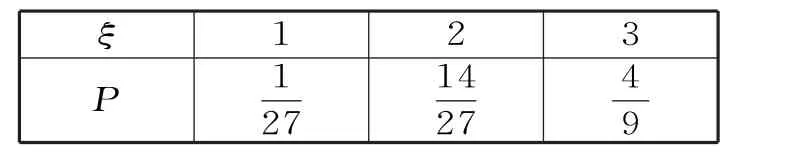
表1

小结：(1)计算古典概型的基本事件数量时要确保彼此是等可能的;(2)求分布列时应先弄清变量的所有可能取值,还要注意到概率之和为1。

2.概率模型的直接考查。

例2 根据以往统计资料,某地车主购买甲种保险的概率为0.5,购买乙种保险但不购买甲种保险的概率为0.3,设各车主购买保险相互独立。

(Ⅰ)求该地1位车主至少购买甲、乙两种保险中的1种的概率;

(Ⅱ)X表示该地的1 0 0位车主中,甲、乙两种保险都不购买的车主数,求X的期望。

分析：计算较复杂事件的概率常用方法有:(1)将其分成若干互斥事件的和;(2)正难则反,先计算其对立事件的概率。而认准概率模型则往往一击中的,简化计算。

解：记A表示事件“该地的1位车主购买甲种保险”;B表示事件“该地的1位车主购买乙种保险但不购买甲种保险”;C表示事件“该地的1位车主至少购买甲、乙两种保险中的1种”;D表示事件“该地的1位车主甲、乙两种保险都不购买”。

(Ⅰ)P(A)=0.5,P(B)=0.3。因为C=A+B,所以P(C)=P(A+B)=P(A)+P(B)=0.8。

小结：二项分布与超几何分布的区别在于,前者是独立重复实验,强调事件每次发生的概率不变,而后者则是对有限产品的次品抽查检验,是一种典型的古典概型。

3.线性回归分析。

例3 一台机器可以按各种不同的转速运转,其生产的物件有一些会有问题,每小时生产有问题物件的多寡,随机器转速而变化,表2中的数据是几次试验的结果。那么,当转速为1 0 r/s时,是否可以预知每小时生产有问题物件数呢?若实际生产中所允许的每小时最大有问题物件数为1 0,那么机器的转速不得超过多少?

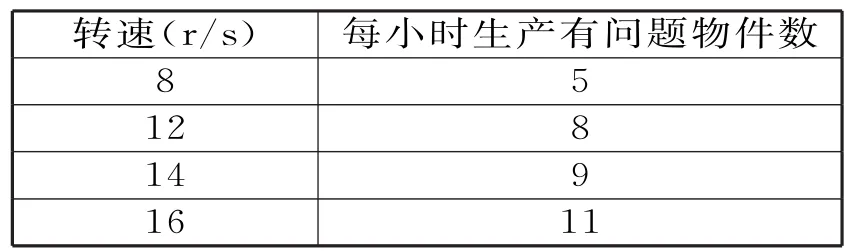
表2

分析：判断两个变量是否线性相关,在高中阶段主要靠画散点图观察。

解：用x表示机器转速,y表示每小时生产有问题物件数,那么4个样本数据为(8,5)、(1 2,8)、(1 4,9)、(1 6,1 1),画出散点图(图略)观察可知这四个点大致分布在一条直线上,可以认为这两个变量具有线性相关关系,于是回归直线的斜率0.7 2 86,a==,所以所求的回归直线方程为y=0.7 2 86x-0.8 5 75。

x=1 0时,y≈6.4,即当转速为1 0r/s时,可以预知每小时生产有问题物件数大约为6.4件;根据公式y=0.7 2 86x-0.8 5 75,要使y≤1 0,则需要0.7 2 86x-0.8 5 75≤1 0,解得x≤1 4.9 0 19,即机器的转速不能超过1 4.9 0 19r/s。

4.独立性检验。

例4 在对人们的休闲方式的一次调查中,共调查了1 2 4人,其中女性7 0人,男性5 4人。女性中有4 3人主要的休闲方式是看电视,另外2 7人主要的休闲方式是运动;男性中有2 1人主要的休闲方式是看电视,另外3 3人主要的休闲方式是运动。

(1)根据数据建立一个2×2列联表;

(2)判断性别与休闲方式是否有关系。

参考公式及临界值表(表3)如下:

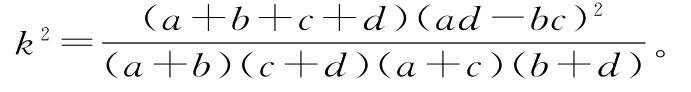
表3

分析：独立性检验是用调查数据来确定甲、乙两个事物是否相关的一种方法,解题关键是要整理出4个数据,即“甲且乙”,“甲且非乙”,“非甲且乙”,“非甲且非乙”。

解：(1)如表4所示的2×2列联表。

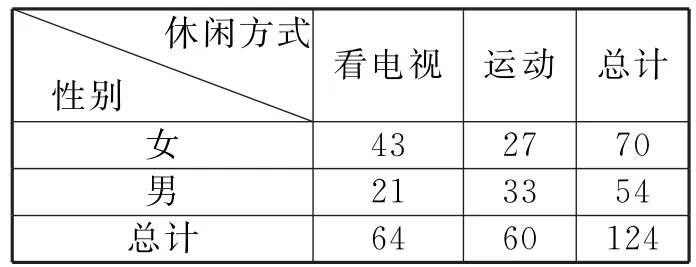
表4

因为k≥5.0 2 4,所以有理由认为假设“休闲方式与性别无关”是不合理的,即有9 7.5%的把握认为“休闲方式与性别有关”。

小结：独立性检验只能得出甲、乙是否相关,以及有多大把握认为其相关,但得不出甲发生时乙发生的概率。

(责任编辑 刘钟华)