复数知识结构与拓展
■河南省南阳市第一中学 郑书芬
复数知识结构与拓展
■河南省南阳市第一中学 郑书芬
一、知识结构

二、结构分析
复数内容在高考中一般会以选择题的形式单独命题,重点是代数运算,属于容易题。高考考纲要求:(1)理解复数的概念,理解复数相等的充要条件;(2)了解复数的代数表示法及其几何意义;(3)能进行复数代数形式的四则运算,了解两个具体复数相加、减的几何意义。复习时重视“化虚为实”的思想方法,切忌盲目拔高要求。
三、典例分析
题型一:复数的有关概念
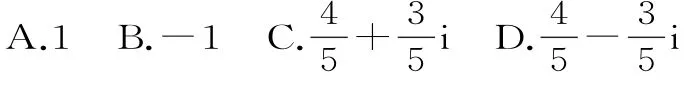
方法规律:(1)复数的分类、复数的相等、复数的模及共轭复数的概念都与复数的实部和虚部有关,所以解答与复数相关概念有关的问题时,需把所给的复数化为代数形式,即a+bi(a,b∈R)的形式,再根据题意列出实部、虚部满足的方程(组)即可。(2)求复数模的常规思路是利用复数的有关运算先求出复数z,然后利用复数模的定义求解。
题型二:复数代数形式的四则运算
例2 已知a,b∈R,i是虚数单位,若(1+i)(1-bi)=a,则
答案解析:因为(1+i)(1-bi)=1+b+(1-b)i=a,又a,b∈R,所以1+b=a且1-b=0,得a=2,b=1,所以
方法规律:复数的加法、减法、乘法运算可以类比多项式的运算,除法关键是分式的分子和分母同乘以分母的共轭复数,注意要把i的幂写成最简形式。
题型三:复数的几何意义
例3 设复数z1,z2在复平面内的对应点关于虚轴对称,已知z1=2+i,则z1z2=( )。
A.-5 B.5 C.-4+i D.-4-i
答案解析:因为z1=2+i在复平面内的对应点的坐标为(2,1),又z1与z2在复平面内的对应点关于虚轴对称,则z2在复平面内的对应点的坐标为(-2,1),即z2=-2+i,所以z1z2=(2+i)(-2+i)=i2-4=-5。
易错防范:(1)判定复数是实数时,仅注重虚部等于0是不够的,还需考虑它的实部是否有意义。(2)两个虚数不能比较大小。(3)利用复数相等a+bi=c+di列方程时,应注意a,b,c,d∈R的前提条件。(4)注意不能把实数集中的所有运算法则和运算性质照搬到复数集中来。例如,若z1,z2∈C,就不能推出z1=z2=0;z2<0在复数范围内有可能成立。
(责任编辑 刘钟华)

