算法框图知识结构与拓展
■河南省南阳市第一中学 马东宇
算法框图知识结构与拓展
■河南省南阳市第一中学 马东宇
一、知识结构

二、结构分析
算法思想作为数学的一种基本思想,就是探求解决问题的一般性方法,并将解决问题的步骤用具体化、程序化的语言加以表述,主要作用是使计算机能代替人完成某些工作,这也是学习算法的重要原因之一。本部分高考的命题思路是:(1)求程序框图的执行结果;(2)确定条件结构中的条件与循环结构中的控制变量,完善程序框图。另外,本部分命题背景新颖,重点内容突出,如程序框图的执行结果与条件判断等,但题目难度不超过中等程度,复习时应重基础,控制好难度。
三、典例分析
题型一:程序框图的基本结构
例1 (2 0 1 7年福州调研)阅读如图1所示的程序框图,运行相应的程序,若输入x的值为1,则输出y的值为( )。
A.2 B.7
C.8 D.1 2 8

图1
方法规律:(1)对条件结构,无论判断框中的条件是否成立,都只能执行两个分支中的一个,不能同时执行两个分支。(2)利用循环结构表示算法,第一,确定是利用当型循环结构还是直到型循环结构;第二,准确表示累计变量;第三,注意从哪一步开始循环。弄清进入或终止的循环条件、循环次数是做题的关键。
题型二:程序框图的识别与完善
例2 执行如图2所示的程序框图,若输出k的值为8,则判断框内可填入的条件是( )。
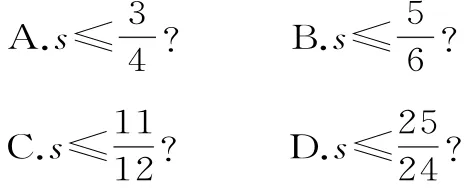
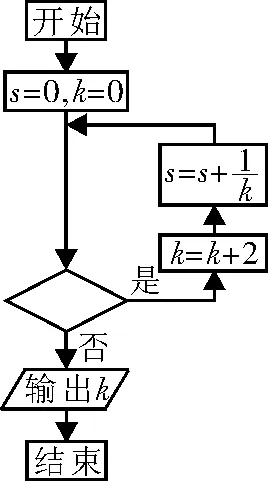
图2
方法规律:(1)要明确程序框图的顺序结构、条件结构和循环结构;(2)理解程序框图的功能;(3)要按框图中的条件运行程序,按照题目的要求完成解答。
题型三:基本算法语句
例3 根据图3所示的算法语句,当输入x的值为6 0时,则输出y的值为( )。
A.2 5 B.3 0 C.3 1 D.6 1

图3
方法规律:(1)本题主要考查条件语句、输入语句、输出语句与赋值语句,要注意赋值语句一般格式中的“=”不同于等式中的“=”,其实质是计算“=”右边表达式的值,并将该值赋给“=”左边的变量。(2)解决此类问题关键要理解各语句的含义,以及基本算法语句与算法结构的对应关系。
易错防范:(1)赋值号左边只能是变量(不是表达式),在一个赋值语句中只能给一个变量赋值。(2)注意条件结构与循环结构的联系:循环结构有重复性,条件结构具有选择性,没有重复性,并且循环结构中必定包含一个条件结构,用于确定何时终止循环体。(3)当型循环与直到型循环的区别:直到型循环是“先循环,后判断,条件满足时终止循环”;而当型循环则是“先判断,后循环,条件满足时执行循环”。两者的判断框内的条件表述在解决同一问题时是不同的,它们恰好相反。
(责任编辑 刘钟华)


