让数学学习插上理想的翅膀——数形结合在教学中的运用

薛 武

（福建福清市江镜玉桂小学，福建福清 350316）

让数学学习插上理想的翅膀
——数形结合在教学中的运用

薛 武

（福建福清市江镜玉桂小学，福建福清 350316）

小学生普遍存在动手能力不强、理解能力差、注意力不集中，上课容易分心的情况，在教学中如果能采用数形结合的思想进行授课，充分利用数形结合的形象性、灵活性、综合性的特点，使学生加深对知识的理解，就能更好地为数学的学习打好基础，提高数学的应用能力。

数形结合；透彻；清晰；创造；全面

引言

在许多人眼中，数学是用数字和符号来演绎，给人一种陌生、抽象、枯燥的感觉，因而他们对数学望而生畏。但是数学是有用的，每个人的生活和学习都离不开数学。好的数学教学可以使学生产生兴趣，进而不懈地探索数学的奥秘，而不好的数学教学可能把学生的学习兴趣扼杀在学习的初级阶段。由此可知，小学数学教育对学生学习起始阶段的重要性尤为重要。让每个学生对数学学习产生兴趣，感受数学的价值和数学的魅力，这对于小学数学教师来说，既是一种挑战也是一份责任。而纵观小学教材的各个学段和各个领域，适合渗透数形结合的思想方法比比皆是。

一、数的认识教学利用数形结合——变肤浅为透彻

数的认识分为认识整数、分数、小数三块，可以说小学生对数的认识既熟悉又陌生，熟悉是它的表现形式，陌生的是它所表示的意义。为此对于数的认识这一教学内容，我个人理解为是以理解数的意义为重点，教学时把抽象的数学知识与具象的图形相结合，挖掘和利用其包含的直观成分，就能有效地促进数学的发展。

在《分数的意义》教学中，我们可以创设分苹果的情境：1个苹果平均分给2个人，每人分到这个苹果的多少，你能把它表示出来吗？再让学生根据自己表示“一半”的，说一说你是怎么想的？从而体会到一半也就是分数1/2的表示含义，既把一个苹果平均分成2份，取其中一份。学生通过经历“一半”的创造过程，从而自然而然地引出“一半也可以用1/2来表示”。再让学生在图形中涂出1/2，并让学生说一说你是怎样得到这个图形的1/2的。模仿表示分数1/2的学习过程，用折、涂等方法学习其他分数，直观体会分数表示意义。这样我们利用数形相结合就能将抽象、枯燥的数学，演绎成学生感兴趣的，乐于接受的，又不失数学本质和数学价值的形式，并展示给学生。老师作为辅助者在一旁观察学生学习进度并为有疑惑的学生进行解答，不仅使学生学会了内容，也保护了其自尊心。

二、概念学习时利用数形结合——变模糊为清晰

在小学数学教材中有关数学概念就有一百多个，几乎在每个新知识的起始课都是概念课，可以肯定地说数学概念是基础知识的核心部分，在数学教学中占有极其重要的地位，它的教学不容我们忽视。而在平时教学和教研中我们发现，很多老师对概念教学普遍存在浮光掠影、过于仓促、死记硬背的现象，学生没有真正理解和体会概念真正的内涵，造成效率低下。如果利用数形结合，为学生搭建开放的平台，就会收到意想不到的精彩。

如《乘法的初步认识》教学时出示主题图，通过看图列式，加深了图式的对应思想。一方面通过观察2+2+2+2+2+2+2=14，感知到相同数连加算式很累，甚至说不清楚，从而体验学习乘法的必要性。另一方面让学生通过观察，讲一讲发现了什么以及算式的表示含义，进而明确加数都是2及有7个2相加，此时，建立乘法概念水到渠成。求几个几相加的和是多少，从而引出求几个相同加数的和可以用乘法来表示，再让学生模仿例题来举乘法例子并说明含义，一方面利用数形结合思想，采取学生易于接受的直观、形象、生动的特点展现出乘法的初始状态。另一方面，也适当降低了教学难度，明确乘法是表示求几个几相加的和的意义，这样就可以更直接、更清晰地让学生明确并灵活掌握“乘法”的概念。

三、在解决问题时利用数形结合——变定式为创造

在平时练习和考试中，让学生感到最头疼的问题就是解决问题。在平时教学中，我们经常会发现在解决此类问题时，不管教师怎么努力分析讲解，学生怎么努力，总有那么一部分学生一直感到困惑和迷茫。解决问题由于抽象程度高，学生难以理解，在教学中我们如果“按图索骥”，难以取得良好的教学效果。如采用以形助教，形为手段，数为目的，根据数量之间内在联系，勾勒出相对应的几何形体，把原来抽象、枯燥、复杂的数量关系，变得形象、可视，使问题形象化、简单化，就能更好帮助学生理解和创造。

比如，学校图书馆上午被借出45本书，下午被借出的书比上午多1/5，图书馆一天被借出多少本书？如果单单从题目中去分析数量关系，对大部分学生来说有比较大的难度。如果在审题时，引导学生利用画线段图来帮助分析数量关系，会起到事半功倍的效果。

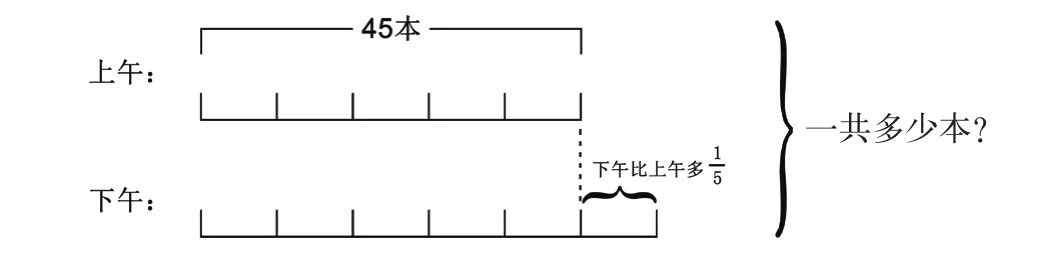
引导学生观察图形，学生很容易弄清题目中的数量关系，学生很容易得到：45+45×1/5，45×（1+1/5），45÷5+45×2，45÷5×(5+6)……利用线段图进行数形转化，将枯燥抽象的问题简单形象化，让看不见的问题为看得见的图形，达到提炼数据、降低难度、排除障碍，变复杂为单一，这样经过一段时间的引导和学习，学生就会意识到图形在解决问题中的“神奇作用”，意识到如果用图来阐述，解题思路就会豁然开朗。

四、在突破重难点时利用数形结合——变片面为全面

数学是一门系统性、逻辑性非常强的学科，一堂课的成功与否，要看教师如何对重点的突破、对难点的解决，学生对重难点的掌握程度，最后评价教师教学质量的优劣。为此我们要提供一切有利的条件、抓住新旧知识联系，使数形结合思想如春雨润物一般，潜入学生思维中，让他们静静地思考，让他们的学习有所触动、感悟，使学生拥有一双火眼金睛，从而养成能找到正确思维的快速通道，让他们的思维闸门得以打开，那么学生的创新灵感就会不断闪现，我们的教学也会收到意想不到的效果。

如平行四边形的面积教学时，先让学生猜：平行四边形的面积可能怎么求？学生猜平行四边形的面积等于两条邻边相乘，教师用PPT演示把平行四边形变成长方形的过程（如图1），进一步引导学生比较，长方形面积与平行四边形面积的大小，从而得出平行四边形面积不能用两条邻边相乘。

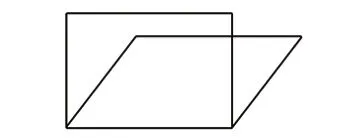
图1

教师进一步引导怎样才能把平行四边形转化成我们已经学过的图形？迫使学生去转化，然后充分让学生表达自己是如何转化的——要通过剪拼把它转化成长方形。在这一个过程中，剪拼的方法很关键，要让学生充分汇报“怎么剪”，再让学生动手按正确方法进行剪拼，这样可以加深转化过程的认识与理解，进一步感知公式的推导过程，有效地培养了学生的探究意识和探究能力。

结语

俗话说：农民光有爱种不出庄稼，还要懂得种庄稼的方法。数形结合就是一种很好的学习方法，它可以丰富学生想象，启迪学生思维，起到“一图抵百语”的效果，它可以让学生展开想象，让学生学习插上理想的翅膀。

[1]张艳红.数形结合思想在小学数学教学中的应用[D].山东师范大学，2016.

[2]张启凤.“数形结合”思想在小学数学教学的应用研究[D].四川师范大学，2016.

[3]胡玉静.数形结合思想在高中数学教学中的应用与分析[D].信阳师范学院，2015.

薛武（1978），男，党员，1996年毕业于福州师范，本科学历。数学中级教师，福州市第十四期骨干教师，福建省骨干教师。工作至今历任过教研员、教导主任、总务主任，并多次被评为福州市、福清市教育系统先进工作者、华罗庚金杯少年数学邀请赛优秀辅导员。