挖掘考题本源，衔接习题求解

张小青

[摘  要] 中考中的一些复合问题与教材内容存在极大的关联，其命题素材来源于教材习题，所以对习题的解题策略进行整合，有助于复合问题的求解. 同时，可以依据教材习题策略对综合问题进行转化. 本文以一道中考几何函数综合题为例，详细讲解衔接习题求解综合题的策略，与读者交流、学习.

[关键词] 几何;函数;综合;图像;提炼;习题

考题呈现

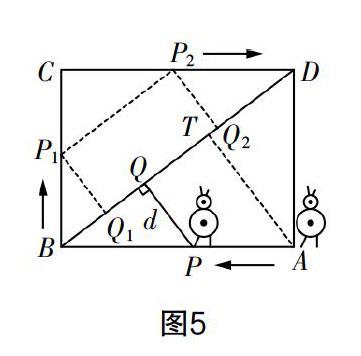
（2017年江苏苏州中考）学校机器人兴趣小组在图1所示的矩形场地上开展机器人操作训练. 已知机器人将从场地的A点出发，在矩形ABCD的四条边上沿着A→B→C→D匀速运动，当机器人到达点D时停止运动. 机器人在运动过程中的速度为每秒1个单位长度，且每当机器人运动至矩形的拐角处都需要1 s的调整时间（在矩形的点B，C拐角处分别需用1 s），设机器人运动过程中的用时为t（s），运动过程中的位置为P，P到矩形的对角线BD的距离（垂线段PQ的长）为d个单位长度，图2为其运动过程中d关于运动时间的函数图像.

（1）试求矩形的边AB，BC的长.

（2）图2曲线上的点M，N分别在线段EF，GH上，已知MN平行于坐标系的横轴，设点M，N的横坐标分别为t₁，t₂，机器人到达P₁处用时为t₁（s），到达P₂处用时为t₂（s）. 如果CP₁+CP₂=7，试求t1和t2的数值.

考题剖析

1. 问题本源剖析

本题从出题形式上来看，为几何材料题，但深度剖析可知问题内容主要由几何图形和函数图像两部分组成，实质上是一道结合了函数图像的动态几何问题，函数图像是对几何运动轨迹的描述. 求解时需要结合函数曲线来深入分析点的运动，然后利用几何性质来求解.

从问题拆分的角度来看，可以将问题内容分为基本的几何图形和函数图像两个部分. 衔接教材习题，可以发现问题的命制来源于苏科版数学教材中的几何问题和函数问题.

几何问题：如图3，在△ABC中，∠BAC=90°，AB=15，AC=20，AD⊥BC，垂足为点D，求AD和BD的长.

原问题虽为矩形内点的运动，但从局部来看依然是一个直角三角形，问题的研究依然需要借助直角三角形的相关性质，其中的垂线段PQ在某些特殊时刻可以看作习题中△ABC斜边上的高AD，求解时需要利用勾股定理建立相关线段的数量关系，这是基于问题几何模型的分析.

函数问题：图4的图像是小红离家后的距离图像，若x表示时间，y表示离家的距离，试说明曲线的实际变化意义.

原问题给出了d关于时间t的图像，这实际上是一次函数图像解决实际问题的应用. 根据点的具体坐标我们完全可以求解出相关一次函数的解析式. 当然，也可以从一次函数的斜率變化情况直接分析线段的长度变化，如图2中EF段所代表的一次函数的斜率为正，则d的长度是增大的过程，分析时就需要对应几何动点d增大的轨迹，而FG是一条平行于坐标横轴的直线，所表示的含义为此时间段内d的长度没有变化，而GH段所代表的一次函数的斜率为负，则表示在该时间段内d的长度在减小，其同样需要对应几何上的相关轨迹.

2. 问题解法剖析

本题有两个小问，第（1）问求的是矩形ABCD中相邻两边的长;第（2）问是求解函数曲线上的对应点的时间值. 解题时单纯地依靠几何性质来求解是不能获得解题思路的，需要从运动角度结合函数图像来分析几何图形，再利用几何图形的性质来求解.

上述求解过程是基于对问题本源的探索，即问题是基本几何和函数图像相结合的综合题，从而实现了动点的定量和定性描述. 几何图形是对动点的轨迹描述，而函数曲线建立了时间与垂线段距离之间的关系. 两个问题分别从几何和函数两个方面进行了设问，对问题的分析也就需要充分结合代数与几何知识. 上述第（2）问的两种解法，解法1是利用几何中的三角形相似性质来求边长，然后求时间;解法2则是直接针对函数图像求解解析式，进而确定点的坐标，根据点的坐标来求时间，它们虽然解法思路不同，但从求解的本质上来看，依然是几何与代数的有效结合，是数形结合思想的应用.

解后思考

1. 深度剖析问题，衔接习题探究

上述题目为几何与函数的综合题，其中涉及基本的几何图形和函数的图像，利用点的运动将两者有机结合起来，建立了问题研究的模型，因此可以将其拆分为教材中常见的两个模型，一是矩形上的垂线段模型，二是函数中长度与时间的曲线模型. 解题时也就需要认真回顾教材模型的研究策略，如矩形的研究可以利用三角形全等、三角形相似，以及勾股定理，而函数的研究需要结合函数的变化趋势、特殊点的坐标等. 另外，教材“一次函数的解决实际问题”章节中给出了一次函数与实际问题的解题策略，即理解函数曲线及变化所代表的实际意义. 这些模型的研究策略对于本题的分析求解有着极为重要的启示作用，因此在平时的学习中，我们要特别注重对教材习题模型的研究策略总结，以用于考题的分析和研究.

2. 全面整合内容，分离提炼问题

本题是一道综合题，涉及众多几何与图形领域的基本知识，如垂线、平行线、三角形的性质和判定、矩形的性质和判定等，同时涉及函数领域中一次函数的图像，两大知识领域是通过动点进行综合的. 而实现问题的求解首先需要充分掌握图形的这些性质特征，并能基于知识联系性对其进行融合，建立起完整的知识体系. 然后是掌握图形的分离策略，能够从复杂图形中基于特定条件分离出基本的图形，或合理地构建基本图形，尤其是动态几何问题，需要化动为静，分离图形. 图形分离的过程需要具备较强的观察能力，该能力的培养可以采用对比分析问题的方式，即把具有类同性的几个问题整合在一起，通过对问题的基本形式和转化条件进行分析，逐步提升自己的数学核心能力.

3. 多角度分析问题，提升思想素养

数学中的综合题不仅仅是知识内容的多重整合，其中也涉及众多的构建思路，即问题知识内容的融合方式，所以从不同的角度分析问题，必然能获得不同的解题信息. 如本题是几何与函数的综合题，从几何角度分析就是几何的动点问题，点运动到图形上的不同位置，必然可以构建不同的模型，如本题第（2）问分别从几何、函数角度进行问题分析，几何角度构建的是关于图形线段长度的关系式，而函数角度构建的是代数方程，解题的思路不同，使用的指导思想也不相同，构造思想和方程思想是其中的思想方法. 思想方法是指导解题思路构建的灵魂所在，是实现问题转化的思想基础，因此，在数学学习中领悟思想方法，促进思想的内化，是学习的关键.

总结

几何、函数综合题是数学几何内容与函数知识的有机结合，其求解策略同样也是两者的综合. 从不同的角度对问题进行思考，在不同的指导思想下可以构建不同的解题思路，获得不同的研究模型. 强化几何综合题的解题策略，不仅需要深度剖析问题本质，还需要全面整合几何与代数的知识内容，掌握复合问题的分离方法，提升数学素养.