注重思维训练 促进分层教学
汤双

[摘 要] 分层走班制教学模式下如何培养C层(优秀)、D层(更优秀)学生的数学思维能力,挖掘潜力,关键是教学策略的选择. 本文从课本一道引题入手,深入浅出地描述了“自主思考,重点展开,分步推进”策略在数学教学中的运用.
[关键词] 数学教学;数学思维;分层教学;教学策略
2015年,笔者所在的学校积极响应《国家中长期教育改革和发展规划纲要(2010-2020年)》中提出的注重因材施教的教育方针,结合学校实际,率先进行了基础教育前瞻性教学改革,开展分层走班制教学活动,力求每位学生在最适合自己的环境中获得基础性学力、发展性学力、创造性学力的最佳发展.
本文以新人教版七年级下册课本第65页“平面直角坐标系”中一道练习题为引,简述开展分层走班制教学模式后,笔者对C层(优秀)、D层(更优秀)学生数学思维能力培养的教学策略.
教学案例
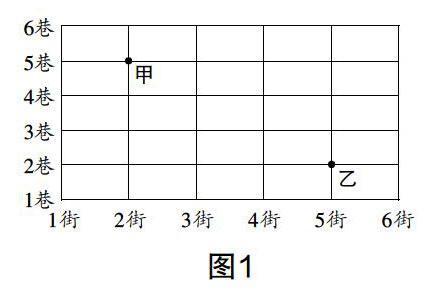
原题:如图1,甲处表示2街与5巷的十字路口,乙处表示5街与2巷的十字路口. 如果用(2,5)表示甲处的位置,那么“(2,5)→(3,5)→(4,5)→(5,5)→(5,4)→(5,3)→(5,2)”表示从甲处到乙处的一种路线. 请你用这种形式写出几种从甲处到乙处的路线.
课例解读:著名的数学大师G·波利亚在探讨教学论时曾经说过:“学习动机的形成有各种各样的原因,其中最重要的是学生‘在学习中寻得快乐.”本题难度低、易理解、发散性强,多数学生能结合圖形找到路线,并通过有序数对将路线描述出来. 在解题过程中,每个层次的学生都享受到成功的快乐,激发出他们研究知识内在联系的欲望.
教学变题
师:如果将引题变为:如图1,若行走路线只能沿线向下和向右运动,则从甲处到乙处有多少种不同的路线?
师:(C层、D层学生)先独立思考2分钟,再以小组为单位,合作完成解答过程.
生1:我们组把满足条件的路线一条条数出来,一共找出18条.
师:这种方法在数学中称为“枚举法”或“穷举法”.
生2:我们组用的也是枚举法,但是我们一共数出20条路线.
师:是吗?两个小组都用了枚举法,结果却不一样. 这是什么原因?
生3:因为枚举法适用于简单问题的求解.
师:很好!本题还有其他解法吗?
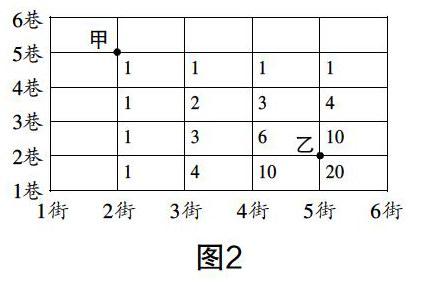
生4:首先,我找出经过每个点的路线,那么能从甲处到乙处的所有路线就是直接到达乙处的各点路线数之和. 详细解法如图2.
师:思考:在这个过程中,解题的关键是什么?
生4:确定能直接从甲处到乙处的点.
师:你的回答真棒!
课例解读:著名的数学大师G·波利亚说:学东西最好的途径是亲自发现它,也就是说最富有成效的学习是学生自己去探索、发现.
变题的起点提高,需要团队合作,思维的火花在合作与碰撞间绽放. 在学生讨论出结果后,教师“画龙点睛”,将学生的回答升华到理论层次,完成新知建构. 这种“自主思考,重点展开,分步推进”的策略成功引领学生在组内、组间开展思考、探究活动,让每个人的注意力都集中在解题中,深刻体验思维结晶.
教学拓展
分层教学的目的是满足不同层次学生的学习需求,让每个层次的孩子“吃饱”“吃好”,最终实现学生的学力提升. 面对C层、D层的学生,教学中,更需要我们精准备课,甄选题目,充分挖掘孩子的学习潜力.
师:如果将引题中“街与巷”的范围扩大,你能找出每列每个节点处满足条件的路线数的规律吗?(要求:C层选做,D层必做)
生5:我们发现,2街一列相邻两个节点间路线都是1,3街越往下走,相邻节点处路线依次增加1,4街越往下走,相邻节点处路线依次增加2,3,4,…5街越往下走,相邻节点处路线依次增加3,6,10,…
师:如果到第n行,各街节点处满足条件的路线分别有多少条?
(大家各自思考1分钟,然后小组讨论)
生7:3街第n行节点的数字是n.
课例解读:著名数学家华罗庚曾说:“就数学本身来说,是壮丽多彩、千姿百态、引人入胜的……”入迷才能叩开思维的大门,智力和能力才能得到发展. 拓展后的引题,难度更大,此时,C层学生已无力招架,D层学生不由自主地沉迷变题,不能自拔. 解答中,同学们围绕变题在组内、组间展开了激烈的讨论,学生的数学素养在激情和体验中得到升华,课堂上呈现了一场精彩绝伦的思维盛宴.
师:如果将“教学拓展”中的变题再加一个条件:如图3,若只能沿线向下和向右运动,则从甲处到乙处的路线中经过丙处的有多少条?
有了刚才一问的铺垫,同学们对此类变题已驾轻就熟,解法如泉水般涌来:
生10:第一段,观察图4,运用加法原理发现从甲处到丙处的路线有3条.
生11:第二段,观察图5,运用加法原理发现从丙处到乙处的路线也有3条.
目前,分层走班模式已在我校开展三年. 三年的课改实践中,我们发现:分层走班模式让数学课堂教学变得更自由、更灵活. “自主思考,重点展开,分步推进”策略在数学课堂教学中的运用让学生的数学思维变得更活跃、逻辑变得更清晰. 学生喜欢这样的课堂,家长认同这样的课堂,教师愿意参与这样的课堂. 笔者有理由相信:这样的教育才是最适合学生的教育,是最好的教育!

