组合荷载作用下输电线路掏挖基础承载特性数值分析

高宇聪，郝冬雪，陈 榕

(东北电力大学 建筑工程学院，吉林 吉林 132012)

组合荷载作用下输电线路掏挖基础承载特性数值分析

高宇聪，郝冬雪，陈 榕

(东北电力大学 建筑工程学院，吉林 吉林 132012)

输电掏挖基础的承载特性是输电线路基础设计和施工中的一个关键问题，它通常会承受上拔与水平荷载的共同作用，现有的理论研究已不能满足工程实际应用的需要。利用有限元软件ABAQUS对在H-V荷载平面内输电线路掏挖基础与周围地基土体共同作用体系的弹塑性有限元模型进行数值计算分析，在改变土参数条件下，研究了3组埋深比的输电掏挖基础的承载力特性与破坏模式，绘制H-V荷载平面内的破坏包络线，研究其变化规律与趋势，并给出破坏包络线的具体方程。

输电线路掏挖基础；组合荷载；承载力特性；破坏包络线

掏挖式基础是将基础的钢筋骨架和混凝土直接浇入由人工掏挖成型的土胎内的一种基础形式，其以天然土构成的抗拨土体与基础自重相互作用而保持基础的上拨稳定。研究试验表明，掏挖基础主要适用于无地下水的硬塑、可塑性黏性土的土质条件，并且掏挖基础具有开挖量小、土体抗力与位移小、节约成本、对周遭地区环境不带来负面影响的众多优点，因此，掏挖基础在输电线路施工中得到广泛应用[1]。

输电塔由于行业特性，所受到的加载相对复杂，输电塔除了要承受自身的重力荷载，还有导线、风等引起的水平荷载，这些荷载最终由塔身传到输电塔基础，导致输电塔基础需同时承受竖向荷载V、水平荷载H的组合加载作用。《架空输电线路基础设计技术规程》[2]中通过添加水平影响系数γE，来应对计算基础上拔荷载时水平荷载对其的影响，而在实际工程施工中，此种方法早已无法满足当前复杂的设计需求。国内学者对掏挖基础的承载力特性也展开了积极的研究：杨剑，高玉峰[3]等人通过数值模拟对输电线路竖向和倾斜式掏挖基础在不同倾角荷载作用下的承载特性和内力分布进行分析；郝冬雪，陈榕[4-5]等人针对掏挖基础极限上拔承载力问题，建立静力学平衡方程，求解不同加载条件下基础的极限上拔承载力，并基于有限元软件ABAQUS建立了有限元数值分析模型，研究了掏挖基础上拔过程中基础底板周围土体的大变形问题。鲁先龙，程永锋[6-9]等人通过大量现场试验，研究在不同原状土体内的掏挖基础的抗拔特性，绘制基础上拔荷载—位移曲线，并选用双切线交法确定基础上拔极限承载力。对于掏挖基础的研究大部分都集中在单向荷载作用下的承载特性，而针对组合加载模式下掏挖基础的承载特性研究仍然较少。崔强[10]基于“m”法，对加翼掏挖基础在水平荷载作用下的承载特性进行力学分析，推导出基础水平位移及基础内力弯矩计算公式。

本文通过大型有限元通用软件ABAQUS，采用荷载-位移法进行加载，研究输电掏挖基础在上拔V与水平荷载H联合作用下的承载力特性与破坏模式。通过变参数计算分析土体模量、抗剪强度指标和基础埋深比对地基基础承载特性的影响，绘制H-V荷载平面内的输电掏挖基础破坏包络线，为输电线路掏挖基础设计提供理论参考。

1 掏挖基础有限元模型

1.1 模型参数

图1 掏挖基础有限元模型

考虑到结构与荷载具有对称性，对整体结构与计算区域的一半建立有限元模型，如图1所示。基础尺寸为：基础埋深为L，主柱直径d=0.8 m，扩底直径D=2 m，扩底高度h=1 m。为消除边界效应的影响，计算域以基础底板中心铅直线向左向右分别取扩底半径的10倍，向下取基础埋深2.75倍[11-13]。模型底部位移全部约束(U1=U2=U3=0)，对称面上约束条件为U3=UR1=UR3=0，模型周围约束水平位移和绕竖轴的转动(U1=U3=UR2=0)。整个计算模型采用三维8节点减缩积分实体单元(C3D8R)。基础周围土体为硬质黏性土，采用Mohr-Coulomb理想弹塑性模型，土体重度为19 kN/m3，弹性模量取值在后面讨论，泊松比取为0.3，根据《架空输电线路基础设计技术规程》中硬质黏性土参数范围，抗剪强度指标c取值在18 kPa～50 kPa，内摩擦角φ在10°～25°内变化，剪胀角为内摩擦角的一半。掏挖基础一般为刚性短桩，因此假设在加载范围内桩身不产生破坏，采用弹性模型，弹性模量取3.25×104MPa，泊松比为0.3。基础—土之间的接触型式定义为摩擦接触，根据规范[2]中坚硬黏性土与混凝土接触面间摩阻系数取值，系数为0.3，桩顶面与刚性表面Tie连接，荷载施加在刚性面的参考点上。采用位移和荷载-位移法进行加载。

1.2 数值模拟与试验结果对比

为了验证数值结果的准确性，利用该建模方法对室内缩比尺模型试验[14]进行能模拟。其中模型尺寸为：D=228 mm，D/d=2.0，L/D=2.0，θ=45°。土体抗剪强度指标由固结快剪试验获得，c=16 kPa，φ=20°，剪胀角ψ=10°，γ=17.7 kN/m3，E=20 MPa。图2为荷载-位移曲线和变形破坏模式的对比。由图可见，数值计算所得极限上拔力较试验结果高约17%。从有限元模拟的地基土体变形破坏模式与试验观测对比发现，变形从基础边缘开始逐渐向外向上扩展至土体表面，地表变形影响半径接近底板半径的3倍，有限元模拟的地基土体变形破坏模式与试验观测接近。此对比表明，该数值模拟能很好地预测掏挖基础的承载力及地基破坏变形模式。

图2 试验与数值模拟结果对比

图3 竖向荷载作用下典型荷载-位移曲线

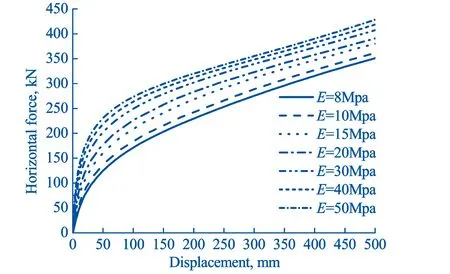
图4 不同土体模量E的水平力-位移曲线

图曲线

图曲线

图7 破坏包络线的绘制

1.3 极限承载力判别方法与弹性模量的影响

从承载能力极限状态上讲，基础极限承载力为其所能承受的最大荷载，即随着荷载的增加，位移增大，当达到一定程度时，微小的荷载增量即会导致很大位移或位移无限开展，此时对应的荷载为极限承载力。但在实际工程中，可能不会允许出现这种程度的变形，一般以达到一定位移作为控制标准。建筑地基基础设计规范[15]与电力行业规范[2]尚未明确给出掏挖基础极限承载力的判断方法。2013年鲁先龙[8]等人通过试验得出，基础在承受上拔荷载作用时，其荷载—位移曲线基本可分为三种类型，如图3所示，三种类型的曲线分别为A、B、C，其中A为“骤降型”，B为“陡变型”，C为“缓变型”。本文中掏挖基础在承受上拔荷载时的荷载—位移曲线为B型，所以采用B型曲线判别方法作为本文判别基础的极限上拔承载力的方法，即：采用曲线的陡变点或陡变后曲线的延长线所对应的荷载值F1作为基础的极限上拔承载力Vult。

以L/D=1，c=32 kPa，φ=20°为例，不同土体弹性模量E时水平力-位移曲线绘于图4。由图4可见，加载初期，随着位移增大，荷载快速增大，当位移达到一定值时，荷载增量减小，荷载位移曲线出现拐点。与上拔情况不同，拐点出现之后，基础仍具备一定的承载能力，即有一定的荷载增量，位移是可控的，并未出现非常大的位移增量。随着土体模量增加，达到拐点所需位移减小。

(1)

式中：Fult为单项上拔、水平极限承载力；γ为土的重度；L为基础埋深；A为基础扩底端面积。

(2)

式中：δu为基础位移；E为弹性模量；D为基础扩底端直径；其他符号同前。

采用相同的判别方法确定基础水平极限承载力。将图4曲线归一化后绘于半对数坐标中，如图6所示，不同弹性模量E时的水平荷载—位移曲线出现陡变点之前基本重合，在陡变点之后，曲线才出现较明显的分散，故弹性模量E的取值对极限水平承载力的确定影响很小。因此，本文在归一化的对数荷载-位移曲线上采用“陡变点”判别方法判定基础水平极限承载力。

2 数值计算与分析

2.1 加载方法与破坏包络线的绘制

为获得竖向与水平荷载空间掏挖基础地基破坏包络线，采用荷载位移法控制方法[11-13]加载，即首先在一个方向施加小于极限值的荷载(水平力H或竖向力V)，保持该荷载不变，然后在另一个方向施加位移(竖向位移uv或水平位移uh)，直至达到此方向极限承载力的标准。由于当基础顶端承受竖向荷载V值接近其极限值Vult时，V-uh加载所绘制的V-H荷载平面内的破坏包络线并不理想，所以为了能够准确的搜寻出Vult附近的破坏包络线，同时进行H-uv反向加载后，与V-uh加载得出的破坏包络线进行比较，考虑施工安全设计，选取两条荷载路径中处在包络线内部的点，作为最后完整的破坏包络线。以L/D=2，黏聚力c=18 kPa，内摩擦角φ=20°为例，如图7所示。

2.2 黏聚力的影响

图8 黏聚力对破坏包络线的影响

图9 45°直线与破坏包络线交点

如图9所示，以内摩擦角φ=20°，埋深比=2为例，在破坏包络线图中做一斜率为45°直线，直线与破坏包络线交点坐标即为水平与上拔荷载，模拟分析45°倾斜荷载作用下掏挖基础的破坏模式。

当基础承受的斜拉荷载达到极限时，如图10所示。基础周围土体局部产生塑性应变：上部土体的塑性应变集中在基础顶部左侧，即承受荷载一侧，塑性应变的形状类似三角形；下部土体的塑性应变集中于基础的扩大端两侧端头，同受力方向一侧的端头对土产生下压荷载，此处端头周围土体的塑性应变集中于端头处，并向下扩散，另一侧对土产生向上的荷载，此处端头周围土体的塑性应变集中于端头，但向上扩散，可见，掏挖基础扩大端对掏挖基础抗倾覆与抗拔起到了关键的作用。综上所述，当保持土体摩擦角φ不变，随着土体黏聚力c的变大，其塑性应变区域减小。

图10 基础等效塑性应变云图

2.3 内摩擦角的影响

为分析土体内摩擦角φ对基础承载力的影响，保持L/D和黏聚力c不变，变化φ=10°、15°、20°和25°进行计算。图11为黏聚力c=32 kPa，某一埋深比时不同内摩擦角对应的V-H荷载空间破坏包络线。随着内摩擦角的增加，破坏包络线外扩，基础抵抗V-H组合荷载的能力增强。在埋深比L/D=1时，随着内摩擦角增加，破坏包络线形状水平向伸长比例稍比竖向大，其它埋深比时，随着内摩擦角增加，破坏包络线基本不改变形状外扩。

图11 内摩擦角对破坏包络线的影响

以埋深比=2，45°倾斜荷载为例，分析其破坏模式。如图12所示，其土体塑性应变变化趋势与2.2基本相同，当保持土体黏聚力c不变，随着土体摩擦角φ的变大，其塑性应变区域减小。

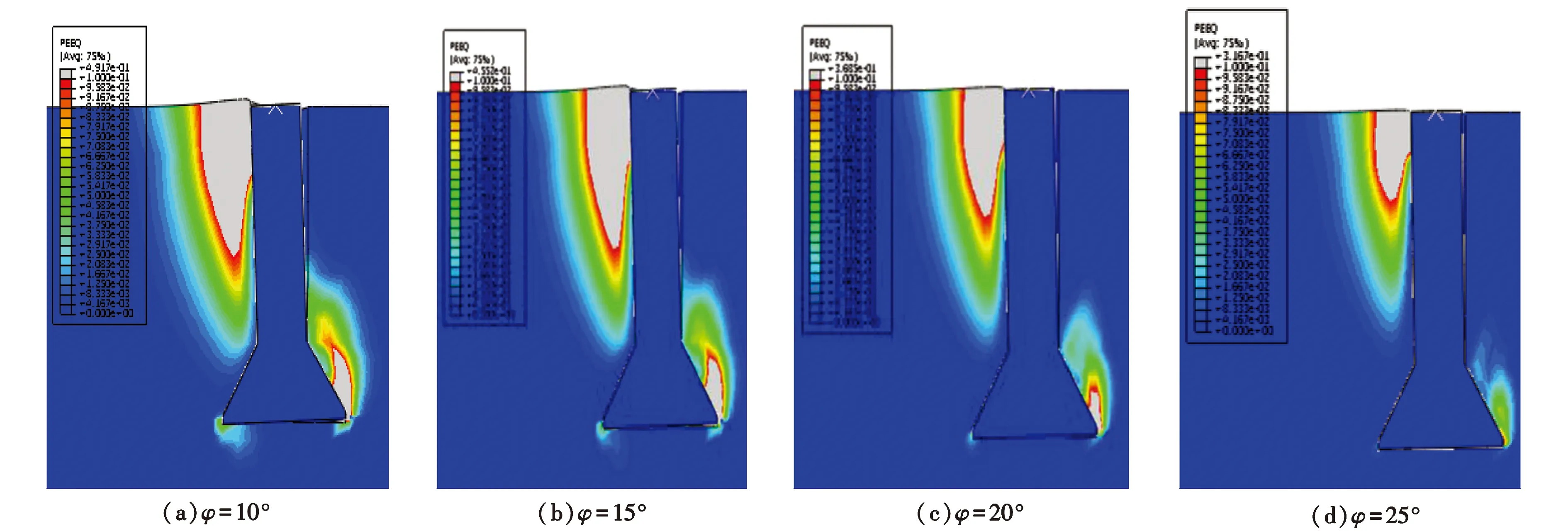
图12 基础等效塑性应变云图

2.4 埋深比的影响

为研究埋深比对掏挖基础破坏包络线的影响，由图13可见，基础的破坏包络线近似椭圆形，当埋深比增加时，破坏包络线向外扩大，并且埋深比由1～2 的荷载增加量与2～3 相比，破坏包络线的变大程度非常明显。

图13 埋深比对基础破坏包络线的影响

以黏聚力c=32 kPa，内摩擦角φ=20°，45°倾斜荷载为例，分析其破坏模式。如图14所示，其塑性应变大部分范围集中于基础一侧，并靠近基础顶部，一小部分集中于基础扩大端，随着基础埋深比的增加，基础一侧的塑性应变范围渐渐向顶部靠拢，扩大端周围的塑性应变范围渐渐变小，如图15所示，基础为倾覆式破坏，随着基础埋深的增加，转动点逐渐上移。

图14 基础等效塑性应变云图

图15 基础位移矢量图

2.5 破坏包络线方程

为了进一步研究破坏包络线的变化规律与变化趋势，现对已得到的破坏包络线进行统一的归一化，如图16所示，在改变土性参数的条件下，掏挖基础埋深比=1、2、3的破坏包络线的落点与形状基本相同，其变化规律与变化趋势也基本相同。

图16 H-V平面内基础的归一化破坏包络线图17 破坏包络线拟合

选取具有代表性落点，对其进行非线性拟合，如图17所示。从图17中可以看出，掏挖基础在V-H荷载平面内的破坏包络线形状近似为椭圆型，这与王志云[16、17]、刘润[18]、文松霖[19、20]等得出的结论相一致。

破坏包络线的方程为

(3)

其中：α、β取值为2时，曲线与原曲线最为接近。

3 结 论

(1)加载方式采用位移控制法，绘制掏挖基础的破坏包络线。通过定性与定量分析，随着土性参数的变大，基础的破坏包络线向外变大。其中随着黏聚力c的变大，每级埋深比荷载增加量却逐渐变小，以靠近水平极限荷载Hult的部分尤为明显；随着摩擦角φ变大时，基础的破坏包络线向外变大，每级埋深比荷载增加量逐渐增大。

(2)埋深比对破坏包络线的影响为：随着基础埋深比的增加，基础的破坏包络线也逐渐变大，并且埋深比由1～2 的荷载增加量与2～3 相比，破坏包络线的变大程度非常明显。

(3)当掏挖基础在承受斜向荷载时，其基础底部扩大端对基础抗倾覆性发挥了巨大的作用，随着基础埋深比的增加，基础的转动点逐渐向上移动。

[1] 陈榕，高宇聪，孟宪彬，等.我国输电线路基础型式对比及其适用性分析[J].东北电力大学学报，2015，35(6)：77-85.

[2] 国家能源局.DL/T 5219-2014架空输电线路基础设计技术规程[S].中国计划出版社，2014.

[3] 杨剑，高玉峰.输电线路掏挖式基础在倾斜荷载作用下的特性[J].工业建筑，2008，38(6)：62-66.

[4] 郝冬雪，张永健，陈榕，等.输电线路掏挖基础极限上拔承载力变分解法[J].岩土力学，2015，36(1)：163-170.

[5] 郝冬雪，樊广森，姜春宝，等.输电线路掏挖基础的抗拔承载特性数值分析[J].水电能源科学，2012，30(8)：151-154.

[6] 鲁先龙，乾增珍，崔强.黄土地基掏挖扩底基础抗拔试验研究[J].岩土力学，2014，35(3)：647-652.

[7] 鲁先龙，乾增珍.戈壁碎石土地基原状土掏挖基础抗拔试验研究[J].土木建筑与环境工程，2012，34(4)：24-31.

[8] 鲁先龙，程永峰.杆塔掏挖基础抗拔研究进展及其设计规范的修订[J].中国电力，2013，46(10)：53-59.

[9] 鲁先龙，郑卫锋，程永锋，等.戈壁滩输电线路碎石土地基全掏挖基础试验研究[J].岩土工程学报，2009，31(11)：1779-1783.

[10] 崔强，鲁先龙，冯自霞.水平荷载作用下加翼掏挖基础承载特性研究[J].地下空间与工程学报，2011，7(3)：457-463.

[11] 栾茂田，武科，范庆来,等.复合加载下桶形基础循环承载性能数值分析[J].海洋工程，2007，25(3)：88-94.

[12] 詹云刚，栾茂田，袁凡凡，等.复合加载下考虑接触作用的地基承载特性数值分析[J].海洋工程，2009，27(1)：40-47.

[13] 张其一，栾茂田，袁凡凡，等.复合加载情况下非均匀地基上矩形基础承载力研究[J].岩土工程学报，2008，30(7)：970-975.

[14] Hao Dongxue，Zhang Jinzhong，Chen Rong.The influence of geometry of pedestal piles in silt on uplift behavior[C].2014 2ndInternational Conference on Mchanical Structures and Smart Materials，Malaysia.

[15] 中华人民共和国住房和城乡建设部.GB50007-2011建筑地基基础设计规范[S].北京：中国建筑工业出版社，2011.

[16] 王志云，王栋，栾茂田，等.复合加载条件下吸力式沉箱基础承载特性数值分析[J].海洋工程，2007，25(2)：52～71.

[17] 王志云，栾茂田，杨庆，等.循环加载条件下吸力式沉箱基础极限承载特性分析[J].大连理工大学学报，2009，49(3)：414-418.

[18] 刘润，王磊，丁红岩，等.复合加载模式下不排水饱和软黏土中宽浅式筒型基础地基承载力包络线研究[J].岩土工程学报，2014，36(1)：146-154.

[19] 文松霖.扩底桩承载力空间屈服包络面的基本特征[J].岩土力学，2006，27(8)：1229-1234.

[20] 文松霖，王孝兵.桩基承载力包络线基本特性数值模拟研究[J].水利水电技术，2011，42(12)：42-46.

NumericalAnalysisofBearingCapacityofExcavatedFoundationofTransmissionLinesSubjectedtoCombinedLoads

GaoYucong，HaoDongxue，ChenRong

(School of Civil Engineering and Architecture，Northeast Electric Power University，Jilin Jilin 132012)

The bearing capacity behaviour of excavated foundation of transmission lines under combined action of uplift load and horizontal load is one of the key issues inconstruction and design of transmission lines.However，the performance of such foundations has not been well understood and related evaluation and design method cannot meet the increasing requirement of engineering practice.Finite element model for the system of foundation and its surrounding homogeneous soil is established based on software ABAQUS to analyze the effects of combined loading.Then comparative numerical computations are performed for changing the property of the soil，The ultimate bearing capacity behaviour and failure mode of excavated foundation under three teams of depth ratio were examined，and print the failure envelope at the H-V load plane by numerical analysis；and inferred the equation of the failure envelope.

Excavated foundation of transmission lines；Combined loading pattern；Bearing capacity behaviour；Failure envelope

2017-01-09

国家自然科学基金项目(51308095)

高宇聪(1988-)，男，硕士，助教，主要研究方向：输电线路基础、岩土力学.

电子邮箱：406882400@qq.com(高宇聪);haodongxue@yahoo.cn(郝冬雪);lg1316cih@126.com(陈榕)

1005-2992(2017)06-0070-09

TM75

A