基于Hilbert包络谱和SVM的齿轮故障诊断

崔天晓，周小龙，刘文浩，王增鹏，马 静，郑佳超

(1.东北电力大学 工程训练教学中心，吉林 吉林132012；2.吉林石化工程设计有限公司，吉林 吉林 132012；3.中国石油吉林石化公司，吉林 吉林 132012；4.敦化市亚联机械制造有限公司，吉林 敦化 133700)

基于Hilbert包络谱和SVM的齿轮故障诊断

崔天晓1，周小龙1，刘文浩2，王增鹏3，马 静3，郑佳超4

(1.东北电力大学 工程训练教学中心，吉林 吉林132012；2.吉林石化工程设计有限公司，吉林 吉林 132012；3.中国石油吉林石化公司，吉林 吉林 132012；4.敦化市亚联机械制造有限公司，吉林 敦化 133700)

针对齿轮振动信号非平稳性和故障特征难以提取的问题，提出一种基于希尔伯特(Hilbert)包络谱和支持向量机(SVM)相结合的故障诊断方法。首先，采用基于镜像延拓的改进经验模态分解(EMD)方法，将齿轮振动信号分解成一系列含有信号特征的固有模态函数(IMF)；其次，根据正交性原理，选取包含信号主要信息的模态分量进行希尔伯特变换并求出包络谱；最后，将包络谱所求出的特征幅值比作为支持向量机分类器的输入来识别齿轮的工作状态。试验结果表明，该方法能有效地识别和诊断出齿轮的工作状态，可应用于该类问题的故障诊断研究。

经验模态分解；镜像延拓；包络谱；支持向量机；齿轮；故障诊断

当机械系统中的齿轮发生故障时，常以其振动信号作为故障诊断对象。然而，由于环境噪声等外界因素和齿轮系统的特性，齿轮振动信号往往表现出非线性和非平稳性的特点[3]，这在很大程度上增加了故障诊断的难度。而常用的故障诊断方法，如：傅里叶变换和小波变换等，在分析该类信号时都具有自身的局限性[4]，难以取得良好的诊断结果。由Huang[5]等人提出的EMD方法由于具有良好的自适应性，因此在处理此类信号的故障诊断方面得到广泛应用[6-8]。但EMD自身的端点效应问题限制了HHT方法在机械故障特征提取及诊断领域的后续发展。

鉴于上述分析，本文提出一种基于改进EMD的Hilbert包络谱和SVM相结合的齿轮故障诊断方法。该方法首先利用镜像延拓抑制EMD分解过程中所产生的端点效应问题，根据各IMF分量间应完全正交的原理，选取包含主要故障信息的IMF并求出相应的包络谱；最后，以不同故障所对应包络谱的特征幅值比作为SVM的输入进行齿轮的故障诊断。试验表明，该方法能有效应用于齿轮故障诊断。

1 改进的EMD

1.1 基于镜像延拓的EMD

由于EMD算法忽略了对信号端点处的约束问题，导致在EMD分解信号的过程中，采用三次样条函数对信号极值点进行插值时，会出现拟合误差，随着分解的不断进行，误差量逐渐增大，最终导致各IMF分量在端点处出现飞翼现象，失去原有物理意义[9]。

在此，采用镜像延拓法解决EMD的端点效应问题。改进EMD能够根据信号的特性自适应地将其分解成一系列IMF，并降低端点效应对于EMD分解准确性的影响。基于镜像延拓EMD方法的具体算法如下：

找出信号x(t)的所有局部极值点，将镜面放置在信号两侧极值点的位置，并将数据序列即为K1、K2。当镜面置于极大值或极小值位置时，分别有：K1=Km(1)、K2=Km(2)以及K1=Kn(1)、K2=Kn(2)。此时，延拓后信号序列为(t，x)：

(1)

(2)

经镜像延拓后，原数据序列和延拓后数据序列形成一封闭的环状曲线，数据的上、下包络线完全由内部数据确定，从根本上避免了端点效应问题，最终输出的时候，只输出两镜面内的数据。

镜像延拓方法从端点效应产生的原因入手，使信号序列的包络线完全由端点的数据确定。同时，对于环形数据列而言，仅一次延拓就可较好地解决端点效应问题，有效提高了EMD的分解效率。

2.2 基于正交性的敏感IMF选择算法

在理想状态下，机械振动信号所包含的各个IMF分量是完全正交的[10]，但由于端点效应的影响，各IMF分量间不可能完全正交。因此，包含信号主要信息的各IMF分量应与原信号有较高的相关系数，可以此作为判别敏感IMF分量的依据。

信号x(t)和其各IMF分量ci(t)之间的相关系数为

(3)

通过计算各阶IMF分量同原信号间的相关系数，并由所分析信号的特点选取门限阈值，从而确定对故障信息敏感的IMF分量。

2 Hilbert包络谱及其特征幅值比

2.1 Hilbert包络谱

由于改进EMD方法所获得的每个IMF分量都是一个单分量的调制信号，因此可以对每个IMF分量进行包络谱分析[11]。

设ci(t)是信号x(t)经EMD分解得到的任意1个IMF分量，对其作Hilbert变换：

(4)

进一步可以求出包络信号：

(5)

对求解此包络信号的相关谱便可获得其包络谱。

2.2 Hilbert包络谱的特征幅值比

对于信号的包络谱而言，能够有效反映旋转机械的周期冲击情况，若对此包络信号选取一合理的评价指标，则可有效反映旋转机械的自身特性。当齿轮箱中的齿轮出现故障时，在包络谱中故障特征频率处会出现相应的谱峰。因此，可将不同齿轮故障在其特征频率处的幅值与齿轮箱中的齿轮(主动齿轮或从动齿轮)在包络谱中的故障特征频率处的幅值比定义为判别齿轮故障的特征幅值比，即

(6)

式中：A(frk)为齿轮箱不同工况下的特征频率处的幅值，其中k=1，2，3，分别代表齿轮正常状态、主从齿轮故障和从动齿轮故障；A(fi) 为齿轮故障状态下的特征频率处的幅值，本文中A(fi) 为从动齿轮故障的特征频率处的幅值；γ为特征幅值比。

3 试验验证

在QPZZ-II型齿轮故障模拟平台上进行了齿轮箱正常运行、主动齿轮磨损和从动齿轮断齿等三种不同工况的试验。实验所用齿轮箱为一级减速器，该齿轮箱由输入轴通过联轴器与驱动电机相连。齿轮箱中驱动齿轮和从动齿轮的齿数分别为55和75，且都为标准直齿轮，输入轴和输出轴的平均转速及转频分别为850 r/min、 523 r/min以及14.14 Hz和10.39 Hz，啮合频率为779 Hz。试验过程中，加速度传感器安装在靠近从动齿轮负载一侧的轴承座上，设置采样频率为5 120 Hz，采样时间为1 s。图1为不同状态下齿轮的振动信号。

图1 不同状态下齿轮时域图

由图1可知，不同工况下，齿轮振动信号在时域中均表现为脉冲冲击，同高斯幅值调制信号相类似。虽然不同故障的时域信号存在细微差异，但是以此为依据不能准确区分故障类型。

为验证所提改进EMD方法的有效性，分别采用两种EMD方法对齿轮箱正常信号进行分析，得到的IMF分量阶数分别为10和14。改进EMD方法由于在一定程度上抑制了端点效应问题的产生，因此在其分解过程中包络拟合误差量有所减少，有效减少了虚假IMF分量。

为有效对比，图2为两种方法分解得到的前8阶IMF分量。对比图2(a)和图2(b)可知，原始EMD方法分解出的IMF分量靠近信号两端点处明显存在异动，在0 s～0.02 s和0.97 s～1 s两个时间区域内产生畸变现象，其中低频IMF分量尤为明显。而改进EMD方法分解出的各IMF分量的端点处没有出现飞翼，同时畸变现象得到较好抑制，所分解出的各阶IMF分量的波形和实际情况更加相符。由此证明改进EMD方法能够更加有效地提取所分析信号的特征信息，保证后续分析的准确性。

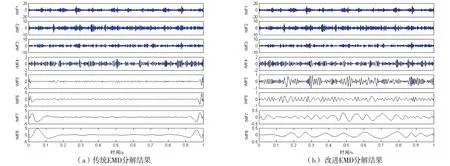
图2 不同EMD方法分解对比

分别对齿轮磨损故障和断齿故障信号进行改进EMD分解，都分解出10阶IMF分量，其中前5阶IMF分量与其原信号间的相关系数，如表1所示。

表1 不同状态下各IMF分量与自身信号的相关系数

由表1可知，虽然所分析的齿轮振动信号处于不同的工作状态，但各种状态信号的前3阶IMF分量集中了其主要故障信息，因此，本文将各状态下齿轮信号的前3阶IMF分量作为敏感IMF分量用于故障特征的提取。不同状态下齿轮振动信号的高频IMF1的包络谱，如图3所示。

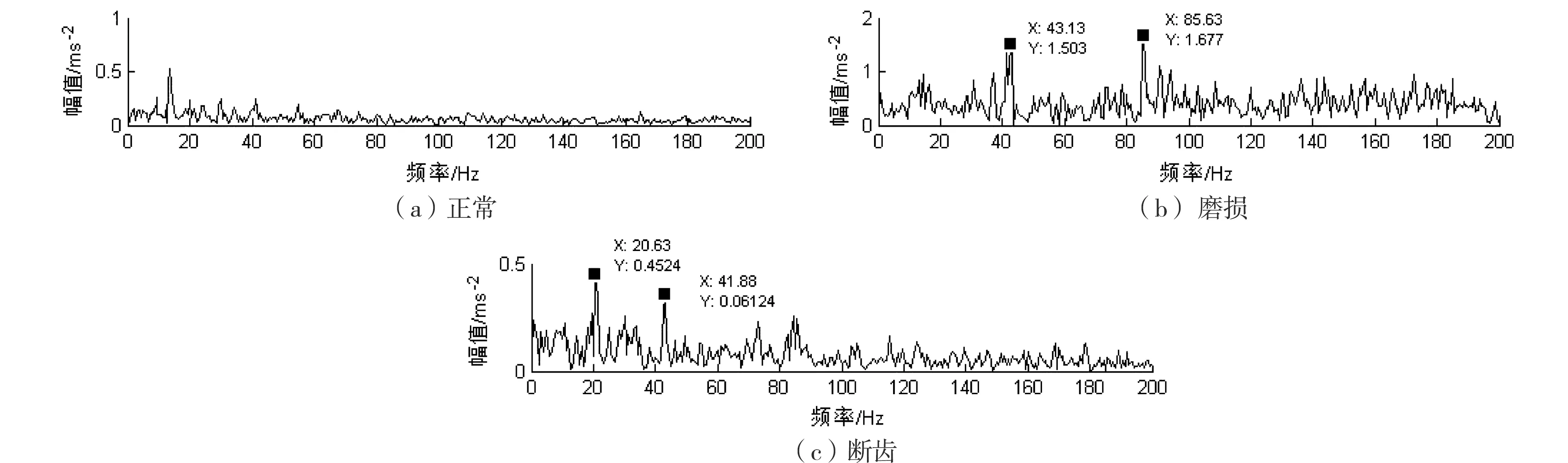
图3 不同状态下齿轮高频IMF1包络谱

由图3可以看出，齿轮磨损和断齿故障信号的包络谱中，其谱峰分别出现在频率为43.13 Hz、85.63 Hz处，以及20.63 Hz、41.88 Hz处，而这正是驱动齿轮的3倍、6倍转频和从动齿轮的2倍、4倍转频，由此可以知，改进EMD所获得的包络谱可以较好地反映出齿轮的故障转频，表2为不同状态下的特征幅值比。

表2 不同状态下的特征幅值比

由表2知，当齿轮处于正常状态齿轮传动平稳，受到的冲击较小，当齿轮出现故障时，通常表现为高频冲击响应特性，且在时域上不连续，呈现冲击与调制特性，因此，相对于磨损和断齿状态，其特征幅值比较小。由于齿轮出现磨损故障，齿轮啮合过程中高频冲击成分增多，所以特征幅值比较正常情况明显增大。

4 基于SVM的齿轮故障诊断

SVM分类器在小样本故障诊断中的分类性能优于神经网络分类器[12]，而目前工程实际应用时所采用的都为小样本的情况，因此，该方法在机械故障诊断领域应用较广[13]。

基于Hilbert包络谱和SVM非齿轮故障诊断方法使用基于镜像延拓的EMD对不同工况下的齿轮振动信号进行预处理，求出不同工况信号的前3阶IMF分量的包络谱，并将其特征幅值比γ作为SVM输入来识别齿轮的工作状态和故障类型。具体诊断步骤如下：

(1)分别采集不同工况下的齿轮振动信号30组，其中采用频率为5 120 Hz，其中任选10组作为SVM的样本，剩余作为测试数据；

(2)采用改进EMD方法对不同工况的齿轮振动信号进行分析，选择各信号的前3阶IMF分量作为分析对象；

(3)对敏感IMF分量进行Hilbert变换，求出其包络谱，并根据公式(6)计算每组信号的特征幅值比γ；

(4)采用2个SVM组成故障诊断分类器。并按照步骤(2)～步骤(3)求出信号的特征向量γ，分类结果以SVM分类器的输出为判别结果。

将SVM1定义决策函数y=+1定义为正常状态，y=-1定义为磨损或断齿故障。将SVM2定义决策函数y=+1为磨损故障，y=-1定义断齿故障。

将之前所确定的训练样本数据和测试样本数据输入SVM模型，其结果为：磨损故障全部识别正确，而正常和断齿故障状态下各有1组数据识别错误，从而确定总体识别正确率为96.67%。引起误判的原因可能是测量过程中的仪器误差或操作误差所引起的，但总体识别效果较为理想。部分识别结果如表3所示。

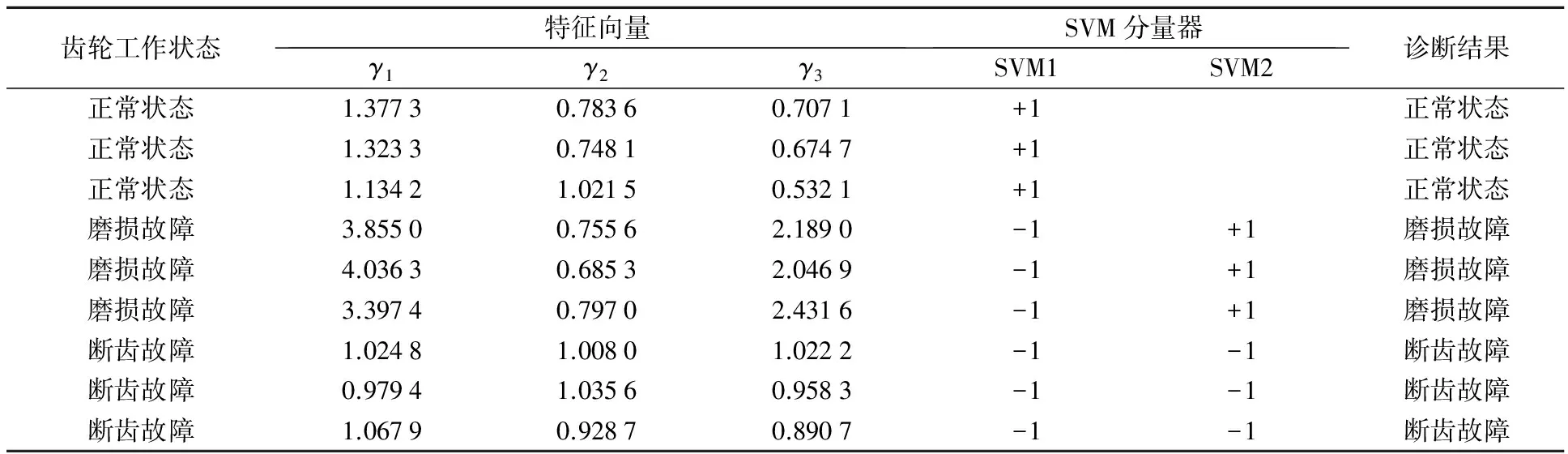
表3 部分测试样本特征向量和SVM识别结果

6 结 论

(1)采用敏感IMF分量所得包络谱的特征幅值比作为特征向量，可以有效增加故障特征信息提取的准确性；

(2)基于Hilbert包络谱和SVM相结合的方法可以有效辨识齿轮的工作状态，为齿轮的故障诊断研究提供了一种切实可行的方法。

[1] 褚福磊，彭志科，冯志鹏，等.机械故障诊断中的现代信号处理方法[M].北京：科学技术出版社，2009：165.

[2] 于德介，程军圣，杨宇.Hilbert-Huang 变换在齿轮故障诊断中的应用[J].机械工程学报，2005，41(6)：102-107.

[3] 谢孟龙.变工况齿轮箱振动信号处理与故障诊断方法研究[D].石家庄：河北科技大学，2013.

[4] 周小龙.希尔伯特-黄变换在故障诊断中的应用[D].长春：长春工业大学，2014.

[5] N.E.Huang，Z.Shen，R.L.Steven，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis[J].Proc.R.Soc.Lond A，1998，454(1971)：903-995.

[6] W.X.Yang.Interpretation of mechanical signals using an improved Hilbert-Huang transform[J].Mechanical Systems and Signal Processing，2008，22(5)：1061-1071.

[7] B.Xu，S.Yuan，M.Wang，et al.Determining impact induced damage by lamb wave mode extracted by EMD method[J].Measurement，2015，65：120-128.

[8] X.Zhao，T.H.Patel，M.J.Zuo.Multivariate EMD and full spectrum based condition monitoring for rotating machinery[J].Mechanical Systems and Signal Processing，2012，27(1)：712-728.

[9] 王传菲，安钢，王凯，等.基于镜像延拓和神经网络的EMD端点效应改进方法[J].装甲兵工程学院学报，2010，24(2)：62-65.

[10] 方琨，王渝，马利兵，等.基于RO-SBM的Hilbert-Huang变换端点效应抑制方法[J].振动、测试与诊断，2013，33(2)：319-324.

[11] 周浩，贾民平.基于EMD和峭度的Hilbert包络解调在滚动轴承故障诊断中的应用分析[J].机电工程，2014，31(9)：1136-1139.

[12] 于德介，程军圣，杨宇.机械故障诊断的Hilbert-Huang变换方法[M].北京：科学技术出版社，2006：155-159.

[13] 周小龙，杨恭勇，梁秀霞，等.基于EMD重构和SVM的滚动轴承故障诊断方法研究[J].东北电力大学学报，2016，36(6)：71-75.

GearFaultDiagnosisBasedonHilbertEnvelopeSpectrumandSVM

CuiTianxiao1，ZhouXiaolong1，LiuWenhao2,WangZengpeng3,MaJing3,ZhengJiachao4

(1.The Engineering Training Teaching Center，Northeast Electric Power University，Jilin Jilin 132012；2.Jilin Petrochemical Engineering Design Co.，ltd.，Jilin Jilin 132012；3.China Petroleum Jilin Petrochemical Company，Jilin Jilin 132012；4.Yalian Machinery Manufacturing Co.，ltd.,Dunhua Jilin 133700)

Aiming at the non-stationary characteristic of the gear vibration signal and the difficulty to get the fault features in its fault diagnosis，a gear fault diagnosis method based on Hilbert envelope spectrum and support vector machine (SVM) is proposed.Firstly，the fault signal is decomposed by empirical mode decomposition (EMD) and a set of intrinsic mode function (IMF) is obtained，which contain the feature of the gear.Then，the envelope spectrums of the sensitive IMFs that selected by the orthogonality principle of each IMFs are obtained.Finally，the characteristic amplitude ratio of the envelope spectrums as input vectors of support vector machine，and identify the gear fault pattern and condition.The experiment shows that this method can identify gear fault patterns effectively and it has a practical value.

Empirical mode decomposition；Mirror extension；Envelope spectrum；Support vector machine；Gear；Fault diagnosis

2017-01-06

崔天晓(1989-)，男，硕士，助理实验师，主要研究方向：金属材料加工.

电子邮箱：2563202296@qq.com(崔天晓)；196389679@qq.com(周小龙)；liu7wenhao@163.com(刘文浩)；362839032@qq.com(王增鹏)；164475236@qq.com(马静)；172424852@qq.com(郑佳超)

1005-2992(2017)06-0056-06

TH17；TH133.33

A