水平管粉煤密相气力输送过程截面涡特性的数值研究

李 铁，刘 勇，杨志瑞，李婧莹

(东北电力大学 能源与动力工程学院，吉林 吉林132012)

水平管粉煤密相气力输送过程截面涡特性的数值研究

李 铁，刘 勇，杨志瑞，李婧莹

(东北电力大学 能源与动力工程学院，吉林 吉林132012)

基于欧拉-欧拉方法，将颗粒动力学理论与修正的颗粒静摩擦力模型相结合，考虑曳力与升力两种相间作用力，及颗粒间碰撞与摩擦力，采用标准湍流模型与小摩擦全滑移边界条件，对水平管内加压密相气力输送过程进行数值模拟。获得了气固两相速度、浓度、湍流强度及压降梯度分布规律，与文献实验规律吻合较好。通过捕捉瞬态两相涡形图，用漩涡耗散理论解释了加压密相气力输送的流场规律，分析了气固两相相互耦合条件下的运动规律。

漩涡耗散；摩擦应力；气力输送；加压密相

干粉进料气流床是一种能够实现加压条件下连续供气的气化装置，是实现煤炭清洁高效利用的核心技术。高压气化要求粉煤必须要在比气化更高的压力下输送，用尽可能少的载气(N2)输送尽可能多的煤粉，一般粉煤浓度高达300 kg/m-600 kg/m，是典型的密相输送[1]。密相气力输运是一种采用低气速对颗粒进行输运的技术，具有低能耗、低磨损、高效率的特点而广泛应用于化工、电力、食品及建筑等行业。

国内外学者对密相气固两相流进行了研究。马胜[2]、谢锴[3]基于电容层析成像技术对工业级水平管粉煤密相气力输送系统的流型进行了研究，结果表明，单一工况下水平管输送流型的不稳定性与固相速度、管道压力等信号存在一定关系，流型的显著变化与压力信号的剧烈波动相对应。Santiago Lain等[4]采用Euler-lagrange方法及k-ε湍流雷诺应力模型对直径为63 mm水平圆管气力输运特性进行了数值模拟，预测数据与试验数据符合较好，说明考虑颗粒与壁面及颗粒间的相互作用的重要性。彭小敏等[5]从试验与数值模拟两方面研究了颗粒粒径对高压密相煤粉气力输送的颗粒流动过程影响，结果显示：较大颗粒粒径使密相气力输送流型从沉积层流向沙丘流，进而向栓塞流的演变过程。由于试验研究受时间、环境等条件限制较大，而数值模拟具有适应性强、不受物理模型和实验模型限制的优点，成为指导水平管加压密相气力输送系统设计和参数优化的有力手段。密相气力输送的数值模型主要有欧拉-拉格朗日模型、双欧拉模型。欧拉-格朗日模型能够准确地模拟颗粒的流动轨迹，但是计算量大，在处理高浓度颗粒流动问题时存在困难。郑建祥等[6-7]将双流体模型及颗粒动力学结合对流化床内超细稠密颗粒气固两相流动进行了模拟，分析了得出了颗粒脉动随颗粒弹性恢复系数增加而变得剧烈，床内颗粒分布更均匀，提高喷口速度有利于颗粒流化的结论。蒲文灏等[8]对现有的颗粒静摩擦力模型进行适当修正，结合颗粒动理学双流体模型模拟了水平管加压密相气力输送流动规律，但其模型中没有考虑升力，Johnson等[9]对双组分相间作用力进行了总结认为：任何双组份流动模型中都应包括曳力和源于密度梯度的扩散力，Slip-shear lift会随着体积分数、相对速度、流体密度、流体粘度、流体速度梯度的增大而增加，大多数情况下不能忽略；李志华等[10]基于CFD理论，采用Fluent 软件建立了水平管内密相散状物料气固两相气力输送数值模型，获得的密相流动状态为气力输送系统的研究和设计提供参考依据。

针对本文的密相气固两相流动，将升力加进颗粒与流体的相互作用中，综合考虑才能更好地反映水平管密相气固两相流动状态。升力主要是由于流体相场内速度梯度而引起的作用在颗粒相的力，比较Slip-shear lift和Spin lift两种升力相对大小，一般情况下，前者较后者大的多；摩擦应力采用蒲文灏等对Johnson等修正后的模型，同时考虑曳力及升力两种相间作用力，并将其与颗粒动理学理论相结合，建立了可以描述加压密相气力输运的气固紊流流动情况的三维两相流模型。该模型充分考虑了颗粒间碰撞和摩擦力作用，气相和颗粒相紊流脉动以及相间相互作用。利用此模型对水平管高压密相气力输运进行了三维数值预测研究。模拟结果与文献试验结果对比，对采用的数值模型进行验证。

1 数学模型

1.1 控制方程

1.1.1 连续性方程

气相

(1)

固相

(2)

1.1.2 动量方程

气相

(3)

固相

(4)

1.1.3 颗粒相拟温度输运方程

(5)

式中：右边第一项为由于颗粒相剪切应力而产生的颗粒脉动能；第二项为沿颗粒相拟温度Θs梯度方向颗粒脉动能的耗散；γΘs为颗粒非弹性碰撞导致的耗散率；φgs为气体和颗粒间脉动能交换。其中，kΘ为颗粒相扩散系数。

1.1.4 湍流输运方程

(7)

式中：当下标i为气相时，下标l为固相；当下标i为固相时，下标l为气相；vi为i相的相平均速度，m/s；k为湍动能，m2/s2；ε为湍流耗数率，m2/s2；Gk，i为i相的湍动能产生项。

1.2 模拟条件与计算方法

本文对内径10 mm、长3 m的水平管，粉煤平均粒径为37 μm和80 μm进行了数值模拟。采用Gidaspow[11]曳力模型：基于Ergun[12]方程以及Wen & Yu[13]的阻力修正公式。

(1)气相边界条件

进口，采用光滑管充分发展湍流流动轴向入口速度：

(8)

(9)

其中：Ug为气相表观气速；αs，in为进口固相的体积分数；Gg为气相的体积流量。出口采用压力出口。壁面采用无滑移边界条件及标准壁面函数。

(2)固相边界条件

进口，采用均匀分布轴向速度：

(10)

(11)

其中：Ms为固相质量流量；μ为固气比。出口采用压力出口。

壁面，Johnson and Jackson[14]提出了颗粒材料与固体壁面边界条件的构成，认为在壁面处颗粒一部分与壁面碰撞，一部分滑移，碰撞发生的动量及能量传输由镜面反射系数决定，并应用于平板剪切。Benyahia[15]对Johnson and Jackson[14]提出的边界条件进行修正，确定了其中镜面反射系数(无法用实验测得)应用于一般问题的过程；Jenkins[16-17]和Louge[18]从力平衡和能量平衡角度给出了颗粒与壁面之间的剪切与脉动边界条件；Soleimani等[19]比较了不同颗粒相壁面边界条件对水平管内气固两相流动特性的影响，认为摩擦系数及恢复系数对流动的影响很大；本文采用Jenkins和Louge的边界条件：小摩擦全滑移极限

τw=μps，

(12)

(13)

(3)模拟工况

固相质量流量：Ms=0.167 kg/s；固相密度：ρs=1 350 kg/m3；输送压力psend=3.3 MPa，其余模拟参数见表1。

表1 数值计算的工况

2 结果与讨论

2.1 模拟结果分析

2.1.1 颗粒相浓度的预测

图1 颗粒浓度分布

颗粒质量流量为Ms=0.227 kg/s，输送压力psend=3.6 MPa，表观气速Ug=6.37 m/s，颗粒平均粒径为80微米时，图1(a)为文献试验采用电容层析成像(ECT)方法得到的颗粒浓度分布；图1(b)为预测的颗粒浓度分布相图。两者都包括悬浮区、过渡区及沉积层，但在模拟结果中过渡区内出现了中间粒子浓度高，壁面颗粒浓度低的情况，可能是所采用的升力模型不够完善，中间两相速度较大，压力偏低而使颗粒向中间聚集的原因，今后将进一步完善。预测结果与试验结果总体符合良好，满足模拟的要求。

2.1.2 颗粒相轴向分布特性

颗粒质量流量为Ms=0.167 kg/s，输送压力psend=3.3 MPa，表观气速Ug=5.88 m/s时，预测的管道4个不同截面处的颗粒浓度分布相图，如图2所示。显然，颗粒的沉积层厚度沿管道流动方向逐渐增高，管道上侧悬浮区域逐渐变大。这是受重力作用的影响使颗粒沉降的结果，与实际的物理过程一致。沉积层内颗粒浓度呈现下高上低现象，可能是因为重力作用下上层对底层颗粒的压实作用，还与沉积层内颗粒的脉动动能及颗粒压力的下降有关。反映沉积层内颗粒相分布并非均匀分布。在X=2 200 mm以后，相图分布基本保持稳定状态，沉积层与悬浮层内的物质交换达到动态平衡状态。

图2 不同截面处颗粒分布

2.1.3 两相速度分布、颗粒相浓度及紊流强度分布

颗粒质量流量为Ms=0.167 kg/s，输送压力psend=3.3 MPa，表观气速Ug=7.85 m/s时，预测的管道垂直方向的不同流动特性，如图3所示。其中图3(a)、图3(b)分别为气相速度和颗粒相速度分布，从图3中看出，两相速度均呈现下部区域速度较高，管道上部区域两相速度较低，主要受到小摩擦全滑移的壁面边界条件影响，也可能与上部气流冲撞形成涡流及二次涡耗散作用的影响有关。图3(c)曲线中颗粒相浓度的分布规律与图3中下高上低的趋势相照应。图3(d)中为垂直方向上颗粒相湍流强度的变化曲线，从下至上，总体呈现增大的趋势，但在底部及顶部由于受到壁面的影响有所下降。

图3 两相速度分布、颗粒相浓度及紊流强度分布

2.1.4 阻力特性的预测

表观气速分别为Ug=4.25 m/s、Ug=5.88 m/s、Ug=6.22 m/s、Ug=6.71 m/s、Ug=7.85 m/s时的单位管长的压降变化，如图4所示。从图4中看出，预测结果与蒲文灏等的试验结果变化走向符合良好，说明本文采用数值模型对研究密相气固两相流具有相当的可信性。

图4 不同表观气速下的压降变化

2.1.5 涡特性对压力损失的影响

图5 z=0截面压力云图

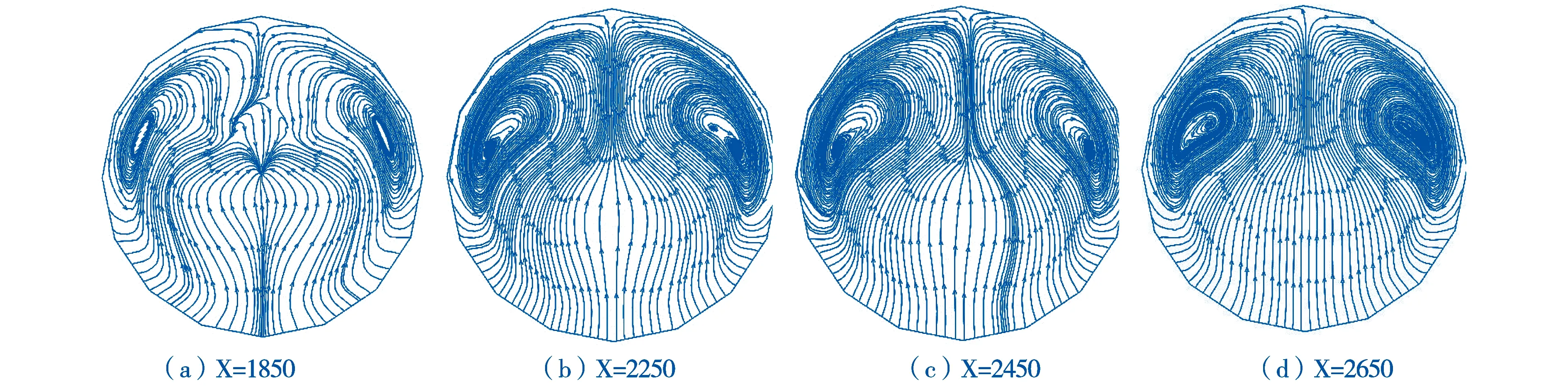
图6 不同截面气相流线图

图7 不同截面颗粒相流线图

颗粒质量流量为Ms=0.167 kg/s，输送压力psend=3.3 MPa，表观气速Ug=5.88 m/s。图5显示部分管长的压力云图，可知压力在管道主流方向逐渐降低。图6、图7分别示出了4个不同截面气相、颗粒相流线图，图中气相流线总体呈现对称分布，并且管道上部区域伴有对称漩涡，但局部存在流线的堆积；沿流动方向涡的强度逐渐增大甚至出现二次涡。颗粒相在重力、气体携带共同作用下由总体沿壁面下滑沉积，并有向中间塌陷的区域，再到塌陷的减弱，出现颗粒相局部区域的非对称聚集，流动状况复杂。在谢锴[3]、彭小敏[5]等的研究中，根据密相输送沙丘流动特征可知密相气力输送中存在周期性变化沙丘流动。造成这种沙丘流的根本原因是气固界面及沙丘内部气固两相作用力的耦合及颗粒间频繁的相互作用。由模拟可以预测，在沙丘流及非沙丘流内部均存在气固两相流动截面涡且具有周期性。因此，拟通过追踪截面涡的发展预测水平密相气力输送管道内的流动、流型及压降的变化规律具有一定的可行性，可对涡型沿主流方向的周期性变化进行深入研究。由图6、图7中非沙丘流型内部的截面涡特征分析可知这种涡反映了气固间、颗粒间的相互作用及涡耗散过程产生的压降。根据这种涡流动在主流方向上变化的周期性可以进而预测整个管长上的压降。本文研究仅对该方法进行定性的概述，深入研究尚需更多不同工况下的模拟数据。

颗粒质量流量为Ms=0.167 kg/s，输送压力psend=3.3 MPa，X=2 200 mm截面处，表观气速分别为Ug=5.88 m/s、Ug=6.22 m/s、Ug=7.85 m/s时，预测的管道同一截面处的气相的流线图。从图8中可以看出随着表观气速的增加，形成的涡的数量和强度增加，图8(b)和图8(c)甚至出现了复杂的非对称涡，这主要是较大速度下在有限空间中的紊流耗散增大。引起管道的喘振现象，表观气速的增加也使得能量损失增大。

图8 不同表观气速下气相的流线图

3 结 论

本文将颗粒动理学理论与修正的颗粒静摩擦力模型相结合，同时考虑曳力与升力两种相间作用力，充分考虑颗粒间的碰撞与摩擦力作用，对水平管内加压密相气力输运的两相流进行数值研究。得到如下结论：

(1)模拟预测了压降梯度变化的规律，前者随后者的增加呈现先减后增的变化趋势，与文献试验数据符合良好。

(2)模拟得到了气固两相的速度分布；获得颗粒相浓度分布，展现了沉积层形成与发展的渐变过程及颗粒相的紊流强度分布。

(3)模拟得到了同一速度管道不同截面下气相、颗粒相的速度涡型图，观察到了气相漩涡的演变过程，沿管道方向不断增强的涡流加剧了压力损失；颗粒相沿管道流动方向或沉积或聚集的复杂流动过程；对比不同表观气速同一截面处的速度流线图，较高表观气速下形成的漩涡更复杂且更强烈，说明压力损失更大。

综上所述，采用本文的数学模型处理高压密相气力输运具有很好的适用性，为高压密相气力输运的设计和优化提供有价值的参考，今后工作将把捕捉周期性变化的沙丘及其运动机理作为研究的方向。

[1] 王辅臣，于遵宏.煤炭气化技术[M].北京：化学工业出版社，2010.

[2] 马胜，郭晓镭，龚欣，等.粉煤密相气力输送流型[J].化工学报，2010，61(6)：1415-1422.

[3] 谢锴，郭晓镭，丛星亮，等.工业级水平管粉煤气力输送的最小压降速度和稳定性[J].化工学报，2013，64(6)：1969-1975.

[4] S.Lain，M.Sommerfeld.Numerical calculation of pneumatic conveying in horizontal channels and pipes：detailed analysis of conveying behaviour[J].International Journal of Multiphase Flow，2012，39：105-120.

[5] 彭小敏，朱立平，袁竹林.煤粉粒径对密相气力输送流型影响的数值模拟[J].燃烧科学与技术，2012，18(4)：375-383.

[6] 郑建祥，刘洪雷.弹性恢复系数对超细颗粒气固流场影响的研究[J].东北电力大学学报，2010，30(6)：10-14.

[7] 郑建祥，吕太.脱硫塔内气固流场数值模拟-稠密颗粒动理学方法[J].东北电力大学学报，2012，32(2)：38-42.

[8] P.U.Wenhao，C.Zhao，Y.Xiong，et al.Numerical simulation of dense pneumatic conveying of pulverized coal in horizontal pipe at high pressure[J].Chemical Engineering Science，2008，65(8)：2500-2512.

[9] G.Johnson，K.R.Rajagopal，M.Massoudi.A review of interaction mechanisms in fluid-solid flows[R].Nasa Sti/recon Technical Report N，1990：27-33.

[10] 李志华，彭宗祥，周云杰，等.散状物料在气力输送管道中的密相流动数值模拟与分析[J].硫磷设计与粉体工程，2012 (5)：32-35.

[11] D.Gidaspow，R.Bezburuah，J.Ding.Hydrodynamics of circulating fluidized beds：Kinetic theory approach[R].Engieering，1991：4-5.

[12] S.Ergun.Fluid flow through packed columns[J].Chem.Eng.Prog.，1952，48(2)：89-94.

[13] C.Y.Wen，Y.H.Yu.Mechanics of fluidization[J].Chem.Eng.Prog.Symp.Series，1966，62：100-111.

[14] P.C.Johnson，R.Jackson.Frictional-collisional constitutive relations for granular materials，with application to plane shearing[J].Journal of Fluid Mechanics，1987，176(176)：67-93.

[15] T.Li，S.Benyahia.Revisiting johnson and jackson boundary conditions for granular flows †[J].Aiche Journal，2011，58(7)：2058-2068.

[16] J.T.Jenkins，M.Y.Louge.On the flux of fluctuation energy in a collisional grain flow at a flat，frictional wall[J].Physics of Fluids，1997，9(10)：2835-2840.

[17] J.T.Jenkins.Boundary conditions for rapid granular flow：flat，frictional walls[J].Journal of Applied Mechanics，1992，59(1)：120-127.

[18] M.Y.Louge，E.Mastorakos，J.T.Jenkins.The role of particle collisions in pneumatic transport[J].Journal of Fluid Mechanics，1991，231(231)：345-359.

[19] A.Soleimani，S.Schneiderbauer，S.Pirker.CFD study of the gas-particle flow in a horizontal duct：The impact of the solids wall boundary conditions[J].Procedia Engineering，2015，102(1)：1026-1037.

NumericalSimulationonCharacteristicsofVortexinCrossSectionofDensePhasePneumaticConveyingofPulverizedCoalinHorizontalPipe

LiTie，LiuYong，YangZhirui，LiJingying

(Energy Resource and Power Engineering College，Northeast Electric Power University，Jilin Jilin 132012)

Particle dynamics theory was combined with modified particle friction stress model，based on Euler-Euler model and standardturbulence model and less friction/all sliding boundary condition，taking into account the drag and lift simultaneously and taking full account of collision and friction between particles，to simulate gas-solid dense-phase pneumatic conveying under high pressure in a horizontal tube.The simulation results included profiles of gas and particle phase velocity，profiles of solids concentration，profiles of the turbulence intensity of particle phase，as well as the value of pressure gradient；the predictions of pressure gradient and granular concentration were in good agreement with the experimental data.The vortex figures of gas and particle in the cross section was also seized and the Eddy dissipation theory was applied to analyze the flow Field DistributionRule of dense-phase pneumatic conveying under high pressure and the motion characteristics of the gas-solids coupling flow.

Eddy dissipation；Friction stress；Pneumatic conveying；High pressure and dense phase

2017-01-06

李 铁(1979-)，女，博士，副教授，主要研究方向：两相流的数值模拟.

电子邮箱：litie0622@163.com(李铁);920781725@qq.com(刘勇);445353083@qq.com(杨志瑞);248562213@qq.com(李婧莹)

1005-2992(2017)06-0062-08

TK01+8

A