概率统计试题图表信息的数据处理探析
温伙其

[摘 要] 通过回顾近几年高考试题,对概率统计试题呈现的图表信息特点进行研究与剖析,阐明各种图表特点与作用,为高中教学提供参考,为学生学习备考提供指导.
[关键词] 高中数学;概率统计;图表信息;数据处理
概率统计是新课程的一个重要标志,教学内容贯穿整个高中数学课程必修和选修内容. 它承载着培养学生收集、整理、描述、分析的数据处理学科素养,也肩负着提高学生应用意识和创新意识的价值.
在社会统计分析应用中,分析数据的一种基本方法是通过图形把它们直观呈现出来,利用表格完成数据规律性排列. 将相关数据作图表示,可以在提取数据重要信息的基础之上,还能够有效地借助图形完成相关数据信息的传递. 这些图表有:二维表格、扇形图、频数(率)分布图(表)、频率分布直方图(折线图)、总体密度曲线(正态分布)、茎叶图等. 本文回顾近几年高考试题,对概率统计试题呈现的图表信息特点进行研究与剖析,阐明各种图表特点与作用,以便为高中教学提供参考,为学生学习备考提供指导.
二维表格
杂乱无章的数据不利于分析数据规律. 统计中经常用表格整理数据,它可以更清楚地了解数据所蕴含的规律,一般用于表示用两个变量对应一种事件(情况). 在高中数学教材中,二维表格常见于古典概型的基本事件、分布列、列联表的K2检验、线性规划的寻找约束条件、循环结构的程序框图.
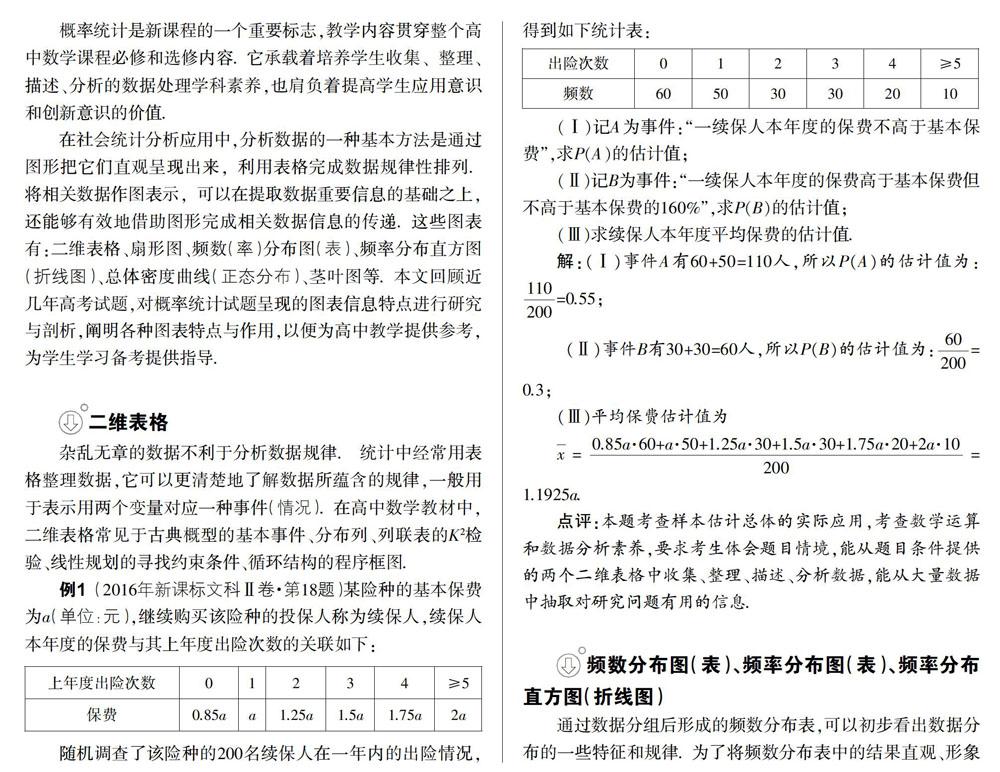
例1 (2016年新课标文科Ⅱ卷·第18题)某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
(Ⅰ)记A为事件:“一续保人本年度的保费不高于基本保费”,求P(A)的估计值;
(Ⅱ)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”,求P(B)的估计值;
(Ⅲ)求续保人本年度平均保费的估计值.
(Ⅲ)平均保费估计值为
点评:本题考查样本估计总体的实际应用,考查数学运算和数据分析素养,要求考生体会题目情境,能从题目条件提供的两个二维表格中收集、整理、描述、分析数据,能从大量数据中抽取对研究问题有用的信息.
通过数据分组后形成的频数分布表,可以初步看出数据分布的一些特征和规律. 为了将频数分布表中的结果直观、形象地表示出来,常常画出频数分布直方图. 而频数分布直方图比较直观,两者放在一起,可以互相补充,从而使我们对数据的频数分布情况了解得更加清楚.
正态分布密度曲线
在频率分布直方图中,随着样本容量不断增大同时组距减少,则组数增加,相应频率的分布直方图,会与光滑曲线较为接近. 该曲线整体为总密度曲线,主要的密度曲线将每一个范围内的百分比数值得以反映,从而确保为我们提供的信息更加精准.
解:正态分布密度曲线图象关于x=μ对称,所以μ1<μ2,从图2中容易得到P(X≤t)≥P(Y≤t). 故选:C.
茎叶图
茎叶图,茎是指中间的一列数,叶就是从茎的旁边生长出来的数. 在样本数据较少时,用茎叶图表示数据的效果较好. 它的特点是没有损失任何样本信息,既能够保留原始数据,又能够展示数据的分布情况,而且可以随时记录,这对数据的记录和表示都能带来方便.
莖叶图可以帮助分析样本数据的分布频率,能够直观显示样本数据的分布规律及集中程度. 通过两组数据的茎叶图比较数据的优劣,先观察“叶”的分布是否具备对称性,找到中位数大小判断高低;然后观察是否具有单峰性,峰值上“叶”的数量决定稳定程度.
散点图
散点图是数据分析的基本工具,在人教A版数学教材出现于必修3第二章:2.3变量间的相关关系. 从散点图的角度研究变量之间的相关关系和线性相关关系的强弱.
例3(2017年北京理科·第17题)为了研究一种新药的疗效,选100名患者随机分成两组,每组各50名,一组服药,另一组不服药. 一段时间后,记录了两组患者的生理指标x和y的数据,并制成下图,其中“*”表示服药者,“+”表示未服药者.
(1)从服药的50名患者中随机选出一人,求此人指标y的值小于60的概率;
(2)从图中A,B,C,D四人中随机抽取两人,记ξ为选出的两人中指标x的值大于1.7的人数,求ξ的分布列和数学期望E(ξ);
(3)试判断这100名患者中服药者指标y数据的方差与未服药者指标y数据的方差的大小. (只需写出结论)
(3)由图知100名患者中服药者指标y数据的方差比未服药者指标y数据的方差大.
?摇?摇总的来说,对统计概率试题中出现的图表信息,一要识别:清楚辨别它属于上述图表中的哪一种?二要用图表:选择恰当合理的图表,方便用于阐述我们要说明的结论;三要画图表:当数据呈现形式杂乱无章时,转化为容易发现特点规律的图表,便于解题.

