追溯数学文化气息 提升学生数学素养


【摘 要】 《普通高中数学课程标准》(2017版)以“立德树人”为重要理念,提出了六大数学学科核心素养,同时要求将数学文化渗透于高中数学课程的始终.数学作为一种文化的传承和积累,它在发展学生数学素养中的教育价值是显而易见的.文章以“两角差的余弦公式” 为例,从教材内容的呈现方式、公式的情景创设、公式证明的策略及公式的应用技巧等方面透析数学文化的融入气息,具体呈现了教材中处处存在数学文化,教学中处处可以渗透数学文化的特点,希望能由微观映射宏观,为广大数学教师教学提供指导和实践的方法,从而有效地改变目前数学文化教育缺失的现状,提高学生整体文化素质和学科素养.
【关键词】 数学文化;数学素养;教材分析;教学思考
随着新课改的不断深入,高考增加了数学文化知识的考查,加之《普通高中课程标准》的颁布,使数学文化的地位进一步得到了加强.相对来说,教师在教学中对数学文化的重视程度滞后,这不仅仅是担心在课堂中融入数学文化会影响教学进度的问题,关键是大部分教师对数学文化了解不深,并且缺少相关的素材.本文通过追溯“两角差的余弦公式”一课所蕴含的数学文化气息,来谈数学文化对学生数学素养的影响,不妥之处恳请指正.
1 从教材内容的呈现方式看数学文化的渗透
由于两角和与差的余弦公式是三角恒等变换的基础,其它复角公式都是在此基础上变换得到的,因此不同版本的教材对两角和与差的余弦公式的产生和推导都非常重视,设计风格也是“八仙过海,各显神通.”
1.1 创设实际问题引入
人教A版,利用章头图片给出实际问题:某城市的电视发射塔建在市郊的一座小山上,如图1所示,小山高BC约为30米,在地平面上有一点A,测得A、C两点间距离约为67米,从点A观测电视发射塔的视角(∠CAD)约为 45°.求这座电视发射塔的高度.
设电视发射塔高CD=x米,∠CAB=α,则
sinα= 30 67 ,…,x= 30tan( 45°+α) tanα -30.
再提出:能不能用sinα把tan( 45°+α)表示出来呢?进而提出更一般的问题,当α,β是任意角时,能不能用α,β的三角函数值把α+β或α-β的三角函数值表示出来?然后引出课题,分别用几何法和向量法推导公式,并配有两个例题.
此设计讲解细腻,环环相扣,课题的产生比较自然,关键是凸显了数学来源于实际,渗透用数学的眼光观察生活,生活中处处有数学的文化积淀.
1.2 问题引进探究拓展
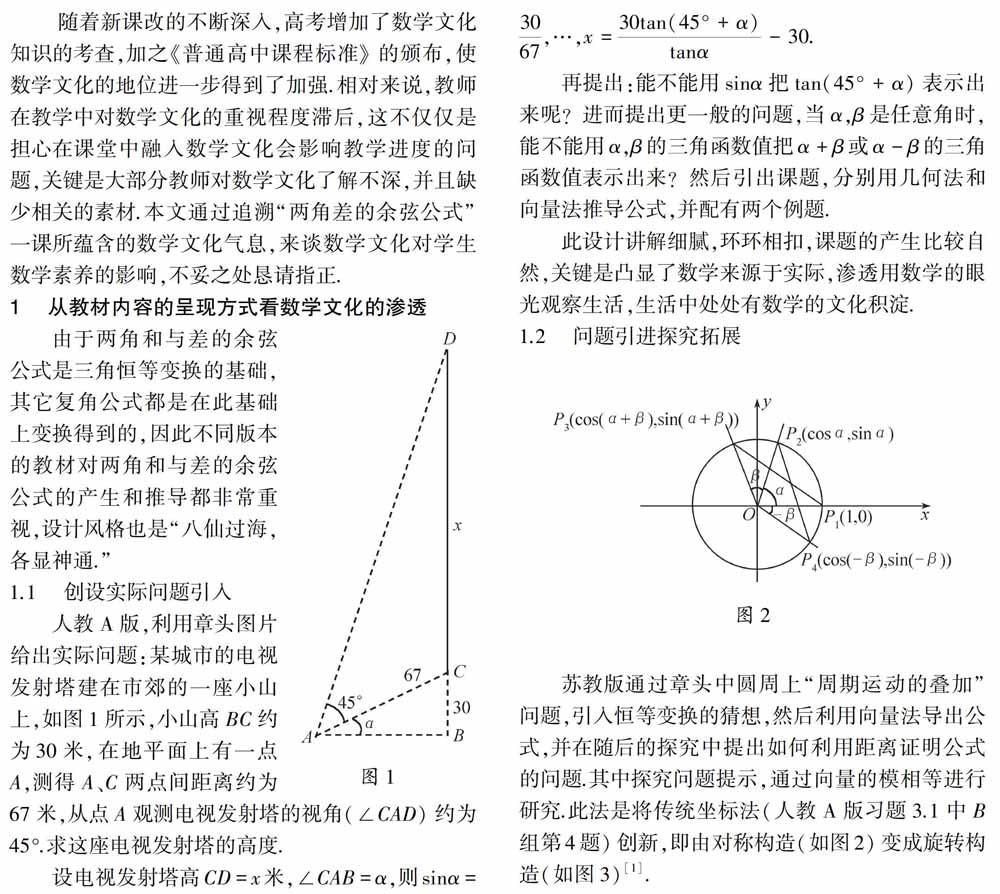
苏教版通过章头中圆周上“周期运动的叠加”问题,引入恒等变换的猜想,然后利用向量法导出公式,并在随后的探究中提出如何利用距离证明公式的问题.其中探究问题提示,通过向量的模相等進行研究.此法是将传统坐标法(人教A版习题3.1中B组第4题)创新,即由对称构造(如图2)变成旋转构造(如图3) [1].
这样设计利于引导学生从向量的角度分析问题,体现了向量的工具价值,而且考虑到了学生接受新知识的认知规律——由特殊到一般,特别是在得出公式之后安排了“探究活动”,突出了《课标》的基本理念,为学生形成积极主动的、多样的学习方式创造条件,以激发学生的数学学习兴趣,鼓励学生在学习过程中养成独立思考和积极探索的习惯.略显遗憾的是构造的问题较陌生,解决思路不自然,有难偏之嫌.同样,在“两角和与差的三角函数”一节开始,就以一方面cosx+sinx=(cosx,sinx)·(1,1),另一方面(cosx,sinx)·(1,1)=…= 2 cos(x- π 4 ).得到cosx+sinx= 2 cos(x- π 4 ),旋即指出:“这是一个有趣的等式,在回答了sinx+cosx可以化为Asin(ωx+φ)的同时,它还告诉我们cos(x- π 4 )可以用x和 π 4 的三角函数来表示”,至此引入课题.这里涉及,第一步不自然的变换技巧,第二步两向量的夹角为何是x- π 4 ,第三步得到的“cos(x- π 4 )可以用x和 π 4 的三角函数来表示” 形式上比较隐晦.学生会是雾里看花,大大削弱了“有趣等式”的体会.1.3 彰显向量的工具性
北师版和湘教版,都是开门见山强调向量的主要作用之一是讨论几何度量问题,进一步复习数量积的意义及其与它们夹角的关系,然后直接运用向量的方法推导公式,并提示可以用诱导公式证明α,β是任意角时公式也成立,可谓惜字如金!人教B版是先给出公式,然后用向量的方法证明.这三种版本的共同点是直接传递“向量是近代数学中重要的和基本的数学概念之一,它属于高中数学的‘双基”的理念,承上启下,不拖泥带水,直接进入主题,不同的是B版的证明逻辑上更为严谨.
2 从引出公式的情景创设看数学文化的渗透
如何自然引出公式是本节课教学的难点之一.虽然《课标(实验)》要求:“经历用向量的数量积推导两角差的余弦公式的过程,进一步体会向量方法的作用.”但在实际教学中若直接利用向量推导公式常常感到牵强,下面给出笔者使用过的四种引出公式的方法供大家参考:
思路1 你能不用计算器求出cos 15°吗?由于我们知道cos45°= 2 2 ,cos30°= 3 2 ,由此我们猜想:cos15°=cos(45°-30°)=?这里是不是等于cos45°-cos30°呢?教师可让学生验证(估算即可),经过验证可知,我们的猜想是错误的!那么究竟是个什么关系呢?cos(α-β)=?这时学生急于想知道这究竟是怎么回事,于是展开新课:我们是利用熟悉的单位圆呢?还是利用刚刚学过的重要工具——向量呢?
效能分析 因为凭直觉得出cos(α-β)=cosα-cosβ是学生容易出现的错误.因此在教学中,引导学生对cos(α-β)的结果进行探究,让学生充分发挥想象力,进行猜想,给出所有可能的结果,然后再去验证其真假,这既展示了数学知识的发生、发展的具体过程,也锻炼了学生的探究创新能力.
思路2 20世纪90年代末美国《数学杂志》开辟了一个专栏“没有文字的证明”,在世界各国产生较大的影响,图4来自广州大学软件所朱华伟老师编写的《无字证明集锦》,你有何发现?
效能分析 正所谓“教学有法,教无定法”,在布鲁纳(美国教育家、心理学家)强烈主张发现学习的时候,奥苏泊尔(美国心理学家)提出有意义的接受学习理论,对布鲁纳过分夸大发现学习的作用提出了强烈的批评.本图由大家熟悉的矩形和直角三角形构成,清晰直观的展示出公式,虽属传授式教学,但快捷省时,且渗透了现代我国数学与世界数学发展的紧密联系,同时有激发学习兴趣的作用.
思路3 中国科学院院士张景中先生从上世纪80年代就开始研究用面积法解决令中学生头疼的几何证明问题,进而形成了几何学的新体系,并且创造了几何定理机器证明的“消点法”.你能看出如图5所示的三角关系吗?
效能分析 以当代数学家的贡献为引子,了解信息技术对数学的影响和我国数学发展成就,激发学生探究图形面积的欲望,虽然面积关系是学生最容易发现的,但在等高等积的处理上仍需教师引导,否则不易得到公式.
思路4 对于基础较好的班级,江苏省前黄高级中学王盈慧老师的做法值得借鉴.如图6所示,倾角为30°的斜坡上,一物体在力F的作用下前进了1m,已知|F|=1N,力F的方向与水平方向成45°角,求此过程中力F所做的功.
设问1 力F与位移s的夹角不是我们熟知的那些特殊角,有办法求此过程中力F所做的功W吗?
将力F正交分解,得水平方向和竖直方向的两个分力F1、F2,将位移s也按同样的方向做正交分解为s1、s2,可以具體计算出W1、W2,再求出和功W.
发现:由F·s=F1·s1+F2·s2,有cos(45°-30°)=cos45°cos30°+sin45°sin30°.
设问2 一般地,斜坡倾角为β,力F的方向与水平方向所成角为α ,还会有类似的结果吗?
效能分析 此法引导学生解决物理问题,从特殊到一般,既归纳出两角差的余弦公式,又体现出物理与数学的关系,利于提高学生研究问题、分析问题和解决问题的视野.
苏东坡有诗云:横看成岭侧成峰,远近高低各不同.同一个事物,从不同的角度看,所得到的表像是不一样的.上面的思路源自于从数量关系、几何直观、面积关系、物理情景等多侧面、多层次地观察和分析,很难说那种方法是最好的,有时简洁是最好的,有时在曲折中前进,学生历经艰难反而体会更深.对教师来说,若能在教学时灵活选择,因材施教,才能利于拓展学生的知识面,利于激发其探究兴趣及学习数学的热情.
3 从证明公式的策略上看数学文化的渗透
学习数学和研究数学令人最感到困惑也是最引人入胜的环节之一,就是如何发现定理及怎样证明定理.公式的证明是本节课的重点,同时也是教学的一个难点,纵览各方面信息发现,值得参考的策 略有:
方案1 归纳——猜想——验证
为了利用向量法推导两角差的余弦公式,教材的编写顺序都是“三角函数——平面向量——三角恒等变形”,这种以牺牲知识的系统性为代价割裂三角函数内容的方法是否值得?先将三角函数学完,再学习平面向量,而在平面向量的应用举例中安排用向量方法探求“两角差的余弦公式”,似乎也未降低向量的工具性价值.
G·波利亚在《数学与猜想》第二卷中指出:“教学必须为发明作准备,或至少给一点发明的尝试.……,并向数学教师们呼吁:让我们教猜想吧!”如在前面思路1,当验证cos(α-β)=cosα-cosβ不一定成立后,继续设置探究问题:很明显cos(α-β)的值与α和β都有关,结合cos( 90°-β)=sinβ=sin 90°sinβ,第二次猜想cos(α-β)=sinαsinβ;取α= 60°,β= 30°,知cos( 60°- 30°)=cos 30°= 3 2 ,
sin 60°sin 30°= 3 2 × 1 2 ,在验明猜想不正确的同时是否发现 3 2 × 1 2 是 3 2 的一半,进而有 3 2 = 1 2 × 3 2 + 3 2 × 1 2 ,即cos( 60°- 30°)=cos 60°cos 30°+sin 60°sin 30°,于是第三次猜想cos(α-β)=cosαcosβ+sinαsinβ,此式对称和谐,一般情况正确的可能性很大,然后取特殊角验证,或用几何画板对任意角的情形进行直观体验,获得学生的认可.
这种办法在立体几何初步中对线面平行和垂直的判定中多次运用,这里照办应当没有什么不妥.借助归纳推理可以培养学生预测结果和探究的能力,对培养创新人才,对学生适应社会能力都非常有利.合情推理也是《课标》倡导的方法,它从具体到一般,符合人们认识问题或事物,总是先认识某种特殊情形,然后过渡到对一般问题或事物的认识的习惯.方案2 几何证法
除了以上思路2和思路3的方法外,最早的古埃及天文学家托勒密在三角函数弦表中的方法(如图7),及公元3世纪亚力山大数学家帕普斯《数学汇编》中给出的证法(如图8,OC=OE=1,CE切半圆O于点H)等 [2],虽还需任意角的推广,但都是很经典的方法.
不难发现,托勒密、帕普斯和人教A版(如图9)的方法,只是形式上不同本质上并无差别.此方案通过适当的数学史和我国数学家的介绍拓宽了学生的视野,也加深了学生对数学研究的亲近感,促进了数学文化的发展.
方案3 坐标法
如图2所示的对称构造法,由三角形全等得, P 1P 3 = P 2P 4 ,进而利用两点间的距离公式推得cos(α+β)=cosαcosβ-sinαsinβ,最后用-β替换β得到差角公式.此法推导思路的产生是一个难点,且并没有直接得到cos(α-)=cosαcosβ+sinαsinβ,另外对P 1、O、P 3及P 2、O、P 4在一条直线上时,还需特别说明.
相比之下,运用如图3的旋转构造,即人教B版中“探究”的方法,则更显优越.
方案4 向量法
引进新的数学工具或知识是简捷求解有关问题的途径 [3].应用数量积推导余弦的差角公式无论是构造两个角的差,还是得到两个角的三角函数值都是容易实现的,难点在当α、β是任意角时公式的證明.可设向量 OP 1 与 OP 2 的夹角为θ,则当0≤α-β≤π时,α-β=θ;当π<α-β≤2π时,α-β=2π-θ.所以,不论α,β为何值,总存在m,n∈[WTHZ]Z,使α-β=2mπ+θ,或α-β=2nπ-θ.利用诱导公式,都有cos(α-β)=cosθ.
该方案通过向量的数量积的定义和坐标运算两种形式求向量的数量积,将二者结合起来,这样做既体现数量积的“形”“数”关系,又充分体现了向量在处理三角函数问题中的工具作用,并且还通过向量数量积的几何意义为两角差的余弦公式提供了几何背景.遗憾的是对任意角时α-β与两向量的夹角之间关系的探讨较难,而冲淡了此法的优越性.
此外,学过余弦定理之后还可以用余弦定理推导,等等.总之,不论是归纳法、几何法、解析法,还是向量法都是以数学对象的直观表象透视其精确的数量关系,不同的推导方法体现出不同的数学特点,不同的巧妙构思得到相同的结果,都有助于培养学生的数学推理能力,也进一步体验了数学的博大精深.
4 从应用公式的技巧上看数学文化的渗透
各版本在例题、练习和习题的配备上大同小异,概括起来有四类:
第一类,运用公式证明“ π 2 -α、π-α、 3π 2 -α”的诱导公式.它不仅是公式的直接运用,关键是让学生体会这些诱导公式都是两角差余弦公式的特例.
第二类,公式的正用.从求特殊角 15°、 75°的三角函数值,到条件求值 (已知两角的正弦或余弦值,求两角差的余弦值),虽是公式的简单应用,但体现了数学语言的魅力,α、β可以是任意角,当然可以表示特殊角、体现了一般到特殊的思想.
第三类,公式的逆用.各版本不仅都有直观结构型如“求sin 95°sin 35°+cos 95°cos 35°的值”的题目,也有需要凑配才能运用公式化简或求最值的型如“f(x)= 3 cosx+sinx”的问题.这些对公式运用来说属逆向思考,但对培养学生化归转化及开拓创新能力非常有益.
第四类,推导方法的运用.因为学生所学的知识可能会很快忘掉,但所学到的解决问题的方法却会使学生受益终生.所以苏教版布置探究拓展题:试用向量法直接推导两角和的余弦公式.希望以此来突出向量的强大威力和培养类比方法解决问题的能力,值得提倡.
因为公式给出的是一种新的运算,对于这种新运算不仅要正用、还有逆用,甚至变用,关键是本节乃两角和与差单元的第一课,所以本节的教学宜慢不宜快,要慢出内含、慢出意识、慢出素养、慢出效率 [4],北师版那种全部给出两角和与差的正余弦公式再应用的编写方式,似乎欠妥.这就相当于怀里抱了一堆自己不甚了解的工具,干活时还要在工具堆里选用,这对于刚接触这件事情的学生来说,相比先学好一个公式然后类比学习其它公式应当更符合学生的认知规律.
5 结束语
综上可以看出,教材中处处存在数学文化,教学中处处可以渗透数学文化.我们教师在教学中缺乏对数学文化的渗透,其主要原因是对数学文化了解不深,不知或不会将其融入教学.如本课的教学还可以融入:公式的对称美,公式的特征分析是攻克公式记忆的有效武器,总结为“酷酷+帅帅”;探究新知精神,要引导学生“大胆猜想,小心求证”,猜想可以,但不能想当然,要培养学生科学严谨的探究精神;养成反思的习惯,追寻公式推导的本质,不外乎是在熟练运用三角函数的定义的基础上,对同一个量“算两次”的技能;提炼思想方法,从贯穿始终的数形结合思想、特殊与一般的思想,到公式推导的分类与整合思想,及公式运用的模型化思想和转化思想,无一不是数学知识的精髓.只有让数学文化始终侵润课堂,学生在数学的学习过程中才会充分体会到数学的本质,才能感受到数学是有趣的,数学是美丽的、是有用的,从而真正提升学生的数学素养.
参考文献
[1] 何卫中.知识载体 能力立意[J].中学数学教学参考(上旬),2011(7).
[2] 俞昕.从变换的角度赏析“两角差的余弦公式”之推导[J].中学数学杂志,2015(3).
[3] 沈文选著.走进教育数学[M].北京:科学出版社,2016.11.
[4] 刘正章.致力教材的实用性 追求教学的高效率[J].中小学数学(高中版),2017(11).

